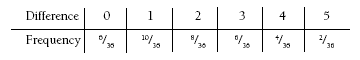This is a level 3 probability and level 2 number activity from the Figure It Out theme series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (537 KB)
find all possible outcomes
investigate if a game is fair
solve problems using subtraction facts
FIO, Level 2-3, Theme: Under the Sea, Horse Racing, pages 18-19
2 classmates
2 dice
Game
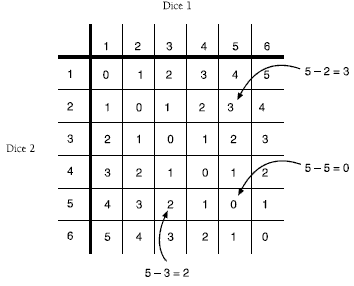
This game focuses on the probability of different outcomes when two dice are thrown. Moves are worked out according to the dice differences, and this table gives the relative likelihood of different sea horses moving:
The relative frequencies of each difference are:
These frequencies are reflected in the distances the different sea horses must travel on the playing board to win. Although sea horse 5 looks an attractive proposition, the chances of throwing the two dice to form a subtraction equation that results in five are small. These varied distances ensure that each sea horse has an equal chance of winning.
Encourage students to explain why some sea horses move more frequently than others. Although they are unlikely to have developed systems such as the table above, many students will be able to offer explanations such as:
“There are lots of ways of getting a difference of one, such as six minus five, five minus four, four minus three, three minus two.”
“There is only one way of getting a five: that’s with six and one.”
Answers to Activity
Game
A game of numbers
Investigation
Answers will vary but will be based on the various ways of getting differences