These are level 3 number, algebra, and statistics problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (291 KB)
use addition strategies to solve problems (Problems 1 and 4)
find outcomes using a table or diagram (Problem 2)
continue a pattern (Problem 3)
Problem One
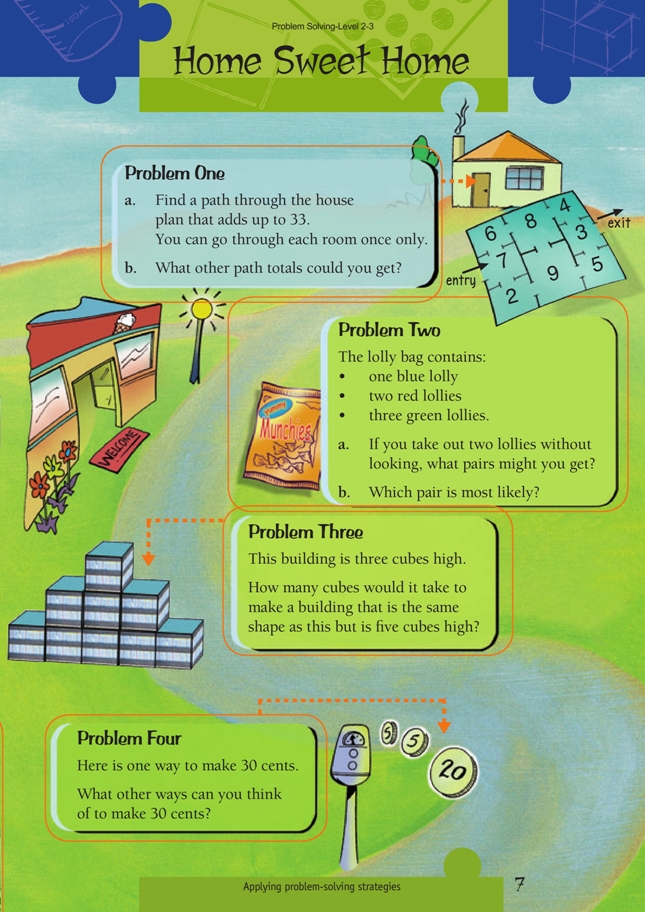
A useful strategy is to add up the numbers in all the rooms, which gives a total of 44. Therefore, the rooms that are not entered must have a total of 11 because 44 – 33 = 11. Possible combinations of rooms that are not entered are 8 and 3, 9 and 2, 5 and 6, and 4 and 7. Students will be able to eliminate two of these possible combinations when they realise that rooms 7 and 3 must be entered.
Rooms 9 and 2 are also eliminated as it would be impossible to travel that way without entering room 3 twice. This leaves only rooms 6 and 5 that must not be entered.
Other totals can be found by systematically working through possible routes:
7 + 6 + 8 + 4 + 3 = 28
7 + 6 + 8 + 9 + 5 + 3 = 38
7 + 2 + 9 + 5 + 3 = 26
Some students may find this diagram of the problem useful:
Encourage students to make up their own house path problems.
Problem Two
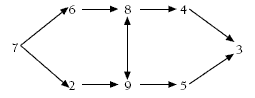
This problem can be modelled using multilink cubes or counters in a plastic container. Students may find all the possibilities by trialling, that is, taking out lots of two lollies and recording the results.
As with other combination problems, using tree diagrams or tables are useful ways to find the solution theoretically. It is helpful to use symbols like r1 and r2 to depict the two red lollies.
Of the 15 possible combinations, six are a pair of one red and one green lolly, so red and green is the most likely pair.
To check whether students have generalised their methods, give them other “lolly in the bag” problems. For example: two yellow, two blue, two red.
Problem Three
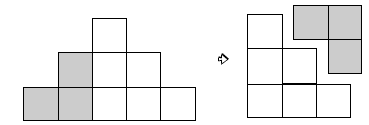
This problem could be solved by building the model with multilink cubes, or students could write a number sentence showing the number of cubes in each layer:
1 + 3 + 5 + 7 + 9 = 25
Some students may notice that the cubes in the illustration could be rearranged to form a square.
More able students could be asked to solve other five-high problems, such as:
Alternatively, they could be asked to find the number of cubes needed for a model that is 10 cubes high.
Problem Four
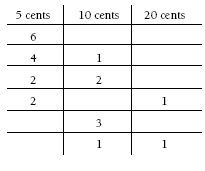
The different ways to make 30 cents could be organised in a table to avoid duplication:
This moneymaking can be extended for more able students. For example:
“How many different ways can you think of to make 40 cents?”
Answers to Problems
1. a. 7 + 2 + 9 + 8 + 4 + 3 = 33
b. Other totals: 26, 28, 38
2. a. blue and red, blue and green,
red and red, red and green,
green and green
b. Most likely: red and green
3. 25
4. 20c, 10c
10c, 10c, 10c,
10c, 10c, 5c, 5c
10c, 5c, 5c, 5c, 5c
5c, 5c, 5c, 5c, 5c, 5c