- ki te whiriwhiri i ngā takirua taunga tauoti hei tuhi kauwhata rārangi torotika e hāngai ana ki tētahi rapanga;
- ki te whiriwhiri, ki te whakamāori hoki i ngā takirua taunga o tētahi kauwhata e whai tikanga ana;
- ki te tūhono i ngā kauwhata rārangi torotika ki ngā whārite pēnei i te ax + ey = c
- ki te whiriwhiri i te takirua taunga tauoti tua‘n’ hei whakaoti rapanga e hāngai ana ki te whārite ax + ey = c.
he pepa tukutuku hei tuhi kauwhata
| kīanga | expression |
| pepa tukutuku | graph paper |
| pūāhua | situation |
| pūtahi | intersect |
| takirua raupapa | ordered pairs |
| takirua taunga | pairs of co-ordinates |
| takirua taunga | co-ordinate pairs |
| tōrite | inequation |
| tua‘n’ | nth |
| tuaka | axis |
| whakarara | parallel |
| whakataetae ihumanea | quiz competition |
| whārite | equation |
- Ko te mahi tuatahi, he whakaatu rapanga ki te kauwhata rārangi, he whiriwhiri hoki i te whārite e hāngai ana ki taua kauwhata.
Ngā Tohutohu
He Tauira Kōrero Mā Te Pouako Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga.
Ka pau i a Mere te $48 ki te hoko i ētahi tōkena me ētahi neketai. E $3 te utu mō te takirua tōkena, e $4 te utu mō te neketai kotahi. He aha ngā kōwhiringa mō te maha o ngā takirua tōkena me te maha o ngā neketai i hokona e Mere?
He maha ngā kōwhiringa mō te maha o ngā tōkena me ngā neketai i hokona e Mere. He aha tētahi kōwhiringa? Akene pea karekau he tokena i hokona e Mere, ka pau āna moni katoa ki te hoko neketai. I tēnei whiringa, e hia ngā neketai i hokona e ia? E 4 tāra te utu mō te neketai kotahi, ka pau te katoa o te $48 ki te hoko neketai. Nō reira, wehea te $48 ki te 4, ka 12. Tekau mā rua ngā neketai i hokona e ia.
Pēhea mēnā karekau he neketai i hokona? E hia ngā tōkena i hokona i tēnei o ngā whiringa? E 3 tāra te utu mō te takirua tōkena, ka pau te katoa o te $48 ki te hoko neketai. Nō reira, wehea te $48 ki te 3, ka 16. Tekau mā ono ngā takirua tōkena i hokona e ia.
Me pēhea te whakaatu i ēnei whiringa e rua ki te kauwhata? Whakaaturia ngā tōkena ki te tuaka pae, ngā neketai ki te tuaka pou.
Kimihia ētahi atu whiringa. Pēhea mēnā e 4 ngā tōkena i hokona e Mere. E hia ngā neketai? $12 te utu mō ngā tōkena e 4, nō reira e $36 e toe ana hei hoko neketai. E 9 ngā neketai ($4 x 9 = 36).
Whakaaturia ngā whiringa katoa ki te kauwhata.
.jpg)
Whakawhitiwhiti kōrero mō te āhua o te kauwhata me tōna whārite. He aha tētahi mea e kitea ana i te kauwhata? E noho ana ngā whiringa katoa ki tētahi rārangi torotika.
Ko te 3x te kīanga hei tātai i te utu mō ngā tōkena. Ko x hei tohu i te maha o ngā tōkena (te tuaka pae o te kauwhata). Whakareatia te maha o ngā tōkena ki te 3 hei tātai i te utu i pau ki te hoko tōkena.
He aha te kīanga hei tātai i te maha o ngā neketai? Ko te 4y. E $4 te utu mō te neketai kotahi. Whakareatia ki te maha o ngā neketai (y – te tuaka pou o te kauwhata), ka hua ko te katoa o te utu i pau ki te hoko neketai.
E hia katoa te moni i pau i a Mere? Ko te $48.
He aha te whārite hei tapiri i te utu mō ngā tōkena me te utu mō ngā neketai? 3x + 4y = 48
Kia pērā anō te mahi hei whakaatu ki taua kauwhata tonu ngā whiriwhiringa e taea ana e Mere mēnā e $36 i pau i a ia. Kia pērā anō te mahi hei whakaatu ki taua kauwhata tonu ngā whiriwhiringa e taea ana e Mere mēnā e $24 i pau i a ia. Kia pērā anō te mahi hei whakaatu ki taua kauwhata tonu ngā whiriwhiringa e taea ana e Mere mēnā e $60 i pau i a ia. Whakawhitiwhiti kōrero mō te āhua o ngā kauwhata. He aha tētahi mea e kitea mai ana i te kauwhata nei? E noho whakarara ana ngā rārangi katoa
- Ka whai anō i te mahi tuatahi ki te whakaatu tōrite ki te kauwhata hei whakaoti rapanga.
Ngā Tohutohu
He Tauira Kōrero Mā Te Pouako Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga.
Ka pau i a Mere te $12 ki te hoko tōkena, neketai hoki. E $3 te utu mō te takirua tōkena, e $4 te utu mō te neketai kotahi. He aha ngā kōwhiringa mō te maha o ngā takirua tōkena me te maha o ngā neketai i hokona e Mere? Ehara i te mea kia pau katoa āna moni.
Aratakina ngā ākonga ki te tuhi kauwhata hei whakaata i te rapanga nei.
I te tuatahi, me tirotiro ngā kōwhiringa mō te maha o ngā tōkena me ngā neketai ka hokona e Mere mēnā ka pau katoa tana $12. He aha tētahi kōwhiringa? Ko tētahi, karekau he tokena, ka pau āna moni katoa ki te hoko neketai. E 4 tāra te utu mō te neketai kotahi, nō reira wehea te $12 ki te 4, ka 3. E 3 ngā neketai i hokona e ia.
Pēhea mēnā karekau he neketai i hokona? E hia ngā tōkena i hokona i tēnei o ngā whiringa? E 3 tāra te utu mō te takirua tōkena, ka pau te katoa o te $12 ki te hoko neketai. Nō reira, wehea te $12 ki te 3, ka 4. E 4 ngā takirua tōkena i hokona e ia.
Me pēhea te whakaatu i ēnei whiringa e rua ki te kauwhata? Whakaturia ngā tōkena ki te tuaka pae, ngā neketai ki te tuaka pou.
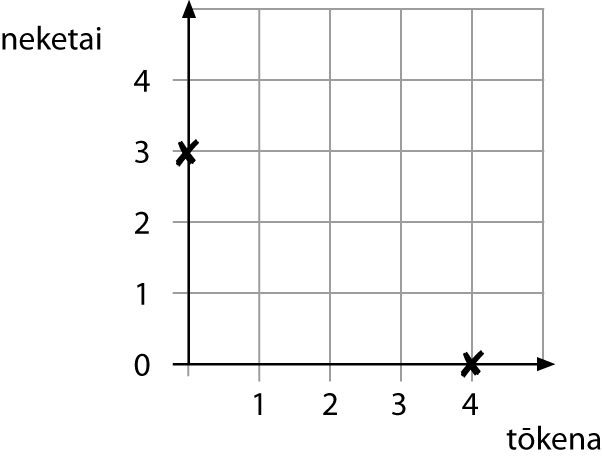
Tuhia he rārangi hei hono i ngā pūwāhi e rua nei. He aha te whārite e hāngai ana ki tēnei rārangi? Mēnā ko te x hei tohu i te maha o ngā tōkena, ko te 3x hei tātai i te utu mō aua tōkena.
Ko te y hei tohu i te maha o ngā neketai, nō reira, ko te 4y hei tātai i te utu mō aua neketai.
Ko te $12 te tapeke o te utu mō ngā tōkena me ngā neketai. Nō reira ka hua mai te whārite nei: 3x + 4 y = 12.
Whakawhitiwhiti kōrero mō ētahi atu otinga o te rapanga. Ko tā te rārangi o te kauwhata, he tohu i ngā kōwhiringa mēnā ka pau i a Mere te katoa o tana $12. He aha ngā kōwhiringa e noho ana ki taua rārangi? Ko te (0,3), arā kāore he tōkena, e 3 ngā neketai. Ko te (4,0) anō tētahi, arā, e 4 ngā tōkena, kāore he neketai. Koia anake. Kāore tētahi atu kōwhiringa tauoti e noho ana ki te rārangi.
Ki te kore e pau i a Mere te katoa o āna moni, he aha ētahi kōwhiringa mō te maha o ngā tōkena me ngā neketai? Whakaaturia ēnei kōwhiringa ki te kauwhata. Tuhia hei takirua raupapa.
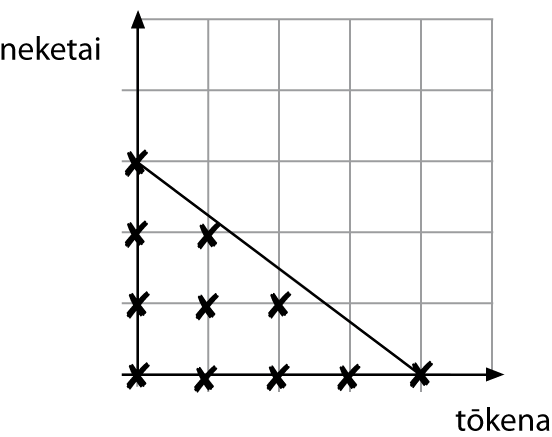
Koia nei ngā kōwhiringa hei takirua raupapa: {(0,0) (0,1) (0,2) (0,3) (1,0) (1,1) (1,2) (2,0) (2,1) (3,0) (4,0)}
Koia nei ngā kōwhiringa mo te x me te y hei otinga tauoti mō te tōrite nei 3x + 4y ? 12.
Kia pērā anō te arataki i ngā ākonga ki te whakaatu i ngā kōwhiringa otinga o ngā tōrite nei ki te kauwhata, me te tuhi anō hei takirua raupapa:
3x + 4y ? 24
2x + 3y ? 12
3x + 5y ? 15
4x + 5y ? 20
- Ko te mahi tuatoru, he whakaatu i ngā whārite pēnei i te ax + ey ki te kauwhata rārangi.
Ngā Tohutohu
He Tauira Kōrero Mā Te Pouako Tuhia te whārite nei ki te papa tuhituhi, ka whakawhitiwhiti kōrero ai mō te rapanga e hāngai ana:
3x + 4y = 27
Anei tētahi whārite hei whakaata i te mahi hokohoko a Mere. He hoko tōkena, he hoko neketai anō tā Mere, e $3 te utu mō te takirua tōkena, e $4 te utu mō te neketai kotahi. He aha te rapanga e hāngai ana? Ka pau i a Mere te $27 ki te hoko tōkena, neketai hoki. He aha ngā kōwhiringa mō te maha o ngā tōkena me te maha o ngā neketai ka hokona e ia?
Me pēhea te whakaatu i te whārite nei ki te kauwhata? Whiriwhiria ngā pito o te rārangi. Ko tētahi kōwhiringa, ka pau te katoa o tana $27 ki te hoko tōkena. Arā, e 9 ngā tōkena, karekau he neketai (27 ÷ 3 = 9).
Aratakina ngā ākonga ki te whakaatu i te whārite nei ki te kauwhata, ki te tūhono anō i te kauwhata ki te rapanga. He aha te takirua raupapa e hāngai ana ki tēnei kōwhiringa? Ko te (9,0)
Whakaaturia ki te kauwhata.
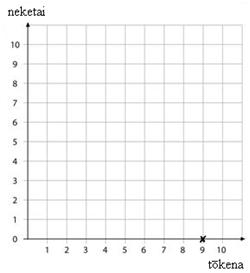
He aha te takirua raupapa e hāngai ana ki tērā atu pito o te rārangi? Ki te pau katoa tana $27 ki te hoko neketai, me wehe te $27 ki te 4 nā te mea e $4 te utu mō te neketai kotahi. Ko te 6¾ tērā (27 ÷ 4 = 6¾) . Nō reira ko te (0, 6¾) te takirua raupapa e hāngai ana.
Kāore e taea ngā neketai 6¾ te hoko. He uaua hoki te whakatau tika i te pūwāhi mō te 6¾ ki te kauwhata. Mēnā kotahi te takirua tōkena i hokona e Mere, e hia ngā neketai? E $24 i pau ki te hoko neketai ($27 – $3 = 24). E 6 ngā neketai e $24 te utu (6 x 4 = 24).
Nō reira he aha te pūwāhi i te kauwhata e hāngai ana ki tēnei kōwhiringa? Ko te (1, 6).
Tuhia tēnei pūwāhi ki te kauwhata. Honoa ngā pūwāhi e rua ki te rārangi torotika.
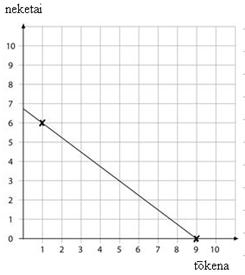
He aha ētahi atu pūwāhi kei runga i te rārangi? Ko te (5, 3).
He aha te kōwhiringa e hāngai ana ki tēnei pūwāhi o te rārangi? E 5 ngā tōkena, e 3 ngā neketai.
Kia pērā anō te arataki i ngā ākonga ki te whakaatu i ngā whārite nei ki te kauwhata, me te tuhi hoki i te rapanga e hāngai ana ki tēnā whārite ki tēnā:
3x + 4y = 28
5x + 2y = 22
5x + 2y = 24
7x + 2y = 32
2x + 3y = 19
3x + 4y = 23
5x + 2y = 17
7x + 3y = 17
- Ko te mahi tuawhā, he whakaatu i ngā whārite pēnei i te ax – ey ki te kauwhata rārangi.
Ngā Tohutohu
He Tauira Kōrero Mā Te Pouako Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga:
I tētahi whakataetae ihumanea, e $3 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $2 mō ia whakautu hē. I te mutunga o te whakataetae, $12 te whiwhinga a tētahi tīma.
Whakawhitiwhiti kōrero mō te whārite e hāngai ana ki te rapanga.
Mēnā ko te x hei tohu i te maha o ngā whakautu tika, he aha te kīanga hei whiriwhiri i te whiwhinga a te tīma mō ēnei whakautu tika? Whakareatia te x ki te 3, nā te mea e $3 te utu mō ia whakautu tika. Arā, 3x.
Mēnā ko te y hei tohu i te te maha o ngā whakautu hē a te tima, he aha te kīanga hei whiriwhiri i ngā tāra ka tangohia atu Whakareatia te y ki te 2, nā te mea e $2 te utu ka tangohia mō ia whakautu hē. Arā, 2y.
Nō reira, he aha te whārite e hono ana i te maha o ngā whakautu tika, ngā whakautu hē, me te whiwhinga o tēnei tīma? Whiriwhiria te utu mō ngā whakautu tika, ka tango ai i ngā tāra ka tangohia atu mō ngā whakautu hē. Ko te $12 te otinga. Arā, 3x – 2y = 12.
Aratakina ngā ākonga ki te whakaatu i te whārite ki te kauwhata rārangi. Mēnā, karekau he whakautu hē a tēnei tīma, e hia ngā whakautu tika? Karekau he utu i tangohia atu, arā, 2y = 0. Nō reira e 4 ngā whakautu tika nā te mea $3 x 4 = $12.
Me pēhea te whakaatu i tēnei pūāhua ki te kauwhata? Whakaaturia ngā whakautu tika ki te tuaka pou (x). Whakaaturia ngā whakautu hē ki te tuaka pou (y). Ko te (4,0) te pūwāhi e hāngai ana ki te pūāhua nei, e 4 ngā whakautu tika, karekau he whakautu hē.
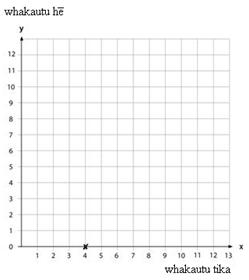
Mēnā e 5 ngā whakautu tika, e hia ngā whakautu hē a te tīma nei? $15 te whiwhinga mō ngā whakautu tika e 5. Nō reira e $3 i tangohia atu kia eke ki te $12 te whiwhinga a tēnei tīma. Engari e $2 ka tangohia mō ia whakautu hē, nō reira kāore e taea te $3 te tango atu.
Pēhea mēnā e 6 ngā whakautu tika? E hia ngā whakautu hē? $18 te whiwhinga mō ngā whakautu tika e 6. Nō reira e $6 i tangohia atu kia eke ki te $12 te whiwhinga a tēnei tīma. E 3 ngā whakautu hē, ka $6. Nō reira mēnā e 6 ngā whakautu tika, e 3 ngā whakautu hē.
He aha te pūwāhi e hāngai ana hei whakaatu ki te kauwhata? Ko te (6,3).
Whiriwhiria ētahi atu pūwāhi hei whakaatu ki te kauwhata. Pēhea mēnā e 8 ngā whakautu tika? Tuhia kia 3 atu anō ngā pūwāhi ki te kauwhata.
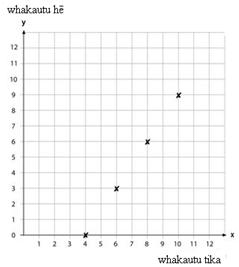
Tuhia te rārangi e hāngai ana ki ēnei pūwāhi. He aha ētahi atu pūwāhi ka tau ki te rārangi? Koia nei ngā takirua raupapa: {(4,0) (6,3) (8,6) (10,9) (12,12) (14,15) …}
Aratakina ngā ākonga ki te tuhi i tētahi anō rārangi ki te kauwhata hei whakaatu i te pūāhua, 14 katoa ngā pātai o te whakataetae ihumanea. Mēnā 14 katoa ngā pātai o te whakataetae ihumanea, me pēhea te whakaatu i tēnei ki te kauwhata. Ko te tapeke o ngā whakautu tika me ngā whakautu hē, ko te 14. Arā, x + y = 14.
He aha ngā pūwāhi e rua kei ngā pito o te rārangi? Mēnā karekau he whakautu tika (x = 0), 14 ngā whakautu hē. Arā te pūwāhi (0,14). Mēnā karekau he whakautu hē, 14 ngā whakautu tika. Ko te pūwāhi (14,0) e hāngai ana.
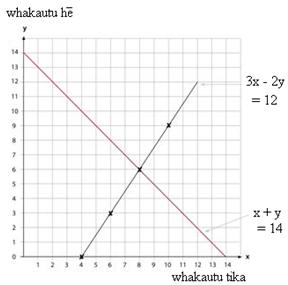
Ki hea pūtahi ai ngā rārangi e rua o te kauwhata? Pūtahi ai i te pūwāhi (9,6).
He aha te tikanga o tēnei pūwāhi? 14 ngā pātai o te whakataetae, ā, $12 te whiwhinga a tēnei tīma (e $3 mō te whakautu tika, ka tangohia te $2 mō te whakautu hē), tērā e 8 ngā whakautu tika, e 6 ngā whakautu hē a tēnei tīma.
Kia pērā anō te arataki i ngā ākonga ki te tuhi whārite, ki te whakaatu hoki i te whārite hei kauwhata rārangi, mō ngā rapanga nei:
- I tētahi whakataetae ihumanea, e $3 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $2 mō ia whakautu hē. I te mutunga o te whakataetae, e $24 te whiwhinga a tētahi tīma.
- Tāngia he kauwhata hei whakaatu i ngā kōwhiringa mō te maha o ngā whakautu tika me ngā whakautu hē e taea ana mō tēnei tīma.
- Mēnā e 25 katoa ngā pātai, tuhia he rārangi ki te kauwhata hei whakaatu i tēnei.
- Nō reira e hia ngā whakautu tika, e hia ngā whakautu hē a tēnei tīma?
- I tētahi anō whakataetae ihumanea, $10 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $9 mō ia whakautu hē. I te mutunga o te whakataetae, e $40 te whiwhinga a tētahi tīma.
- Tāngia he kauwhata hei whakaatu i ngā kōwhiringa mō te maha o ngā whakautu tika me ngā whakautu hē e taea ana mō tēnei tīma.
- Mēnā e 42 katoa ngā pātai, tuhia he rārangi ki te kauwhata hei whakaatu i tēnei.
- Nō reira e hia ngā whakautu tika, e hia ngā whakautu hē a tēnei tīma?
- I tētahi whakataetae ihumanea, e $3 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $2 mō ia whakautu hē. I te mutunga o te whakataetae, e $24 te whiwhinga a tētahi tīma.
- Ko te mahi tuarima, he tirotiro i te whārite o tētahi rārangi torotika e hāngai ana ki tētahi huinga takirua raupapa.
Ngā Tohutohu
He Tauira Kōrero Mā Te Pouako Whakaaturia ngā takirua raupapa e hāngai ana ki te rapanga nei ki tētahi tūtohi (nō nama 4 i runga nei tēnei rapanga).
I tētahi whakataetae ihumanea, e $3 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $2 mō ia whakautu hē. I te mutunga o te whakataetae, $12 te whiwhinga a tētahi tīma.
Anei te tūtohi hei whakaatu i ngā kōwhiringa mō te maha o ngā whakautu tika me ngā whakautu hē e taea ana mō tēnei tīma. Ko x hei tohu i te maha o ngā whakautu tika, ko y hei tohu i te maha o ngā whakautu hē. Whakaotia te tūtohi.
te kōwhiringa x y tua-1 4 0 tua-2 6 3 tua-3 8 6 tua-4 10 9 tua-5 12 12 Aratakina ngā ākonga ki te whiriwhiri i te kōwhiringa 100. Me pēhea te tātai i te kōwhiringa 100. E hia ngā whakautu tika (x) i te kōwhiringa 100. E hia ngā whakautu hē (y)?
He aha te tauira e kitea ana i ngā whakautu tika (x)? Ia otinga, e piki ana mā te 2 (4, 6, 8, 10 …).
Nō reira ko te 2 te tau whakarea i tau o te kōwhiringa. He tāpiri anō hoki i te 2. Titiro ki te tūtohi nei:
te kōwhiringa ngā whakautu tika (x) te whārite tua-1 4 1 x 2 + 2 tua-2 6 2 x 2 + 2 tua-3 8 3 x 2 + 2 tua-4 10 4 x 2 + 2 tua-5 12 5 x 2 + 2 Whāia te tauira, ka tātai ai i te maha o ngā whakautu tika (x) e hāngai ana ki te kōwhiringa 100.
kōwhiringa ngā whakautu tika (x) te whārite tua-1 4 1 x 2 + 2 tua-2 6 2 x 2 + 2 tua-3 8 3 x 2 + 2 tua-4 10 4 x 2 + 2 tua-5 12 5 x 2 + 2 tua-100 202 100 x 2 + 2 Kia pērā anō te tātai i te maha o ngā whakautu hē e hāngai ana ki te kōwhiringa 100.
te kōwhiringa ngā whakautu hē (y) te whārite tua-1 0 1 x 3 – 3 tua-2 3 2 x 3 – 3 tua-3 6 3 x 3 – 3 tua-4 9 4 x 3 – 3 tua-5 12 5 x 3 – 3 tua-100 297 100 x 3 – 3 Me tirotiro ināianei, e hia tara te whiwhinga a te tīma nei mēnā 202 ā rātou whakautu tika, 297 ā rātou whakautu hē. Kia hoki ki te whārite: 3x – 2y = 12, nā te mea $12 te whiwhinga a tēnei tīma.
3x – 2y = 12
(3 x 202) – (2 x 297) = 12
606 – 594 = 12Whakawhitihiti kōrero mō ngā whārite hei tātai i te kōwhiringa tua-‘n’. He aha te whārite hei tātai i te maha o ngā whakautu tika? Ka whakareatia te tau o te kōwhiringa ki te 2, ka tāpiri i te 2.
Nō reira, he aha te whārite hei tātai i te maha o ngā whakautu tika mēnā ko te ‘n’ hei tohu i te tau o te kōwhiringa? x = 2n + 2.
He aha te whārite hei tātai i te maha o ngā whakautu hē? Ka whakareatia te tau o te kōwhiringa ki te 3, ka tango ai i te 3.
Nō reira, he aha te whārite hei tātai i te maha o ngā whakautu hē mēnā ko te ‘n’ hei tohu i te tau o te kōwhiringa? y = 3n – 3.
Kia pērā anō te arataki i ngā ākonga ki te kimi i te whārite hei tātai i te maha o ngā whakautu tika me ngā whakautu hē e hāngai ana ki ēnei rapanga. Whakamahia te whārite hei tātai i te kōwhiringa 1000 mō te maha o ngā whakautu tika me ngā whakautu hē.
- I tētahi whakataetae ihumanea, e $4 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $2 mō ia whakautu hē. I te mutunga o te whakataetae, $12 te whiwhinga a tētahi tīma.
- I tētahi whakataetae ihumanea, $10 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $1 mō ia whakautu hē. I te mutunga o te whakataetae, $120 te whiwhinga a tētahi tīma.
- I tētahi whakataetae ihumanea, e $5 te whiwhinga a te tīma mō ia whakautu tika, ka tangohia te $6 mō ia whakautu hē. I te mutunga o te whakataetae, $15 te whiwhinga a tētahi tīma.