This problem solving activity has a statistics focus.
Rangi is in a hurry to get off to a party.
He grabs two CDs from his CD rack.
If he has 5 Kickin' CDs and 3 Now CDs, is he more likely to have grabbed a pair of Kickin' CDs or one of each?
- Systematically count outcomes.
- Compare the likelihood of events.
- Devise and use problem solving strategies to explore situations mathematically (systematic list, draw a picture, use equipment).
In this problem students should be encouraged to draw combinations, make a systematic list or table, or use equipment to show that they have explored all the possibilities.
The solution shows a systematic approach.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- 8 CD's (or pictures or models) to introduce the problem
The Problem
Rangi is in a hurry to get off to a party. He grabs two CDs from his CD rack. If he has 5 Kickin' CDs and 3 Now CDs, is he more likely to have grabbed a pair of Kickin' CDs or one of each?
Teaching Sequence
- Introduce the problem using models of the 8 CD's. Get students to take turns randomly selecting 2 CD's (with eyes shut or by covering the CD rack). Demonstrate how to systematically record the outcomes (e.g. in a table, by drawing combinations).
After several turns ask the students to make statements about what they have observed. - Pose the problem. Check that the students understand that they need to find all the ways of selecting 2 CD's from the rack of 8.
- As the students work on the problem, in pairs, ask questions that require them to explain how they are counting outcomes and how they know they will find ALL the possible ways.
- Encourage the students to record their solution in a way that will enable them to convince others that they are correct.
- Share written records. Discuss the different approaches (list, pictures)
Extension
Write a CD problem where the answer is equally likely.
Solution
Regardless of their choice of strategy to solve this problem, students should demonstrate that they have explored all possibilities.
In this diagram the 5 Kickin' CDs are shown with white circles (1, 2, 3, 4, 5) and the 3 Now CDs are shown with black circles (1, 2, 3).
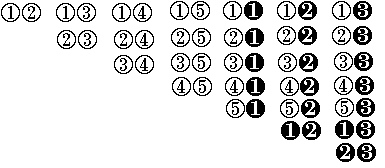
There are 28 ways of taking two CDs from Rangi collection.
There are just 10 ways for Rangi to have grabbed a pair of Kickin' CDs and 15 ways to have grabbed one Now and one Kickin'. So he is more likely to have taken a mixture of Kickin' and Now to the party.
