This problem solving activity has a geometry focus.
Use the half arrow shape as a starting block to produce your own wallpaper friezes. Put this shape into the grid to make a repeating pattern.
How many different repeating patterns can you make?
- Create a repeating pattern using geometric transformations (rotations, reflections, translations).
There is a great deal of mathematics in everyday objects. The patterns on walls are no exception and wallpaper friezes often utilise reflections, translations and rotations. Producing their own friezes gives students the opportunity to explore all of the basic transformations of 2D shapes.
There are three transformations:
- Translations (or shifts)
- Rotations (or turns)
- Reflections
- Grids
- Pictures of wallpaper friezes
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
The Problem
Use the half arrow shape as a starting block to produce your own wallpaper friezes. Put this shape into the grid to make a repeating pattern.
How many different repeating patterns can you make?
Teaching Sequence
- Introduce the problem by looking at some wallpaper friezes – discuss the symmetry that they have and how shapes have been rotated, reflected, and shifted to create a design and/or pattern.
- Introduce the problem shape and the grid to develop the frieze in. Demonstrate how to reflect, rotate and shift one of the half-arrow shapes. Explain that the arrow must be contained within one of the grid squares and demonstrate this. This could also be done digitally.
- As a class develop one of the patterns.
- Pose the problem.
- Let the students investigate the problem, in small groups, using a grid and at least 8 of the half-arrow shapes. Remind them they must put the half-arrow shape in the grid to create a pattern that will repeat indefinitely.
- As the students solve the problem, encourage them to record their findings so that they can share them later. This requires them to either draw or describe the pattern made. Ask questions that focus on the symmetry of the pattern made:
How did you create the pattern?
Have you used reflection in your pattern? Show me?
Have you rotated the shape? Show me?
Have you shifted the shape? Show me how? - Share the patterns students have made.
Have we found them all?
How do you know?
Extension
You might try to find actual wallpaper friezes that match up with the patterns found in the problem.
Ask students to create their own pattern by cutting out a new shape from a rectangular piece of paper, that is the same size as one of the grid squares, and then repeating, reflecting, rotating, and shifting the shape around the grid.
Solution
There are 7 different wallpaper friezes that can be made using the basic block in the picture. They are listed here.
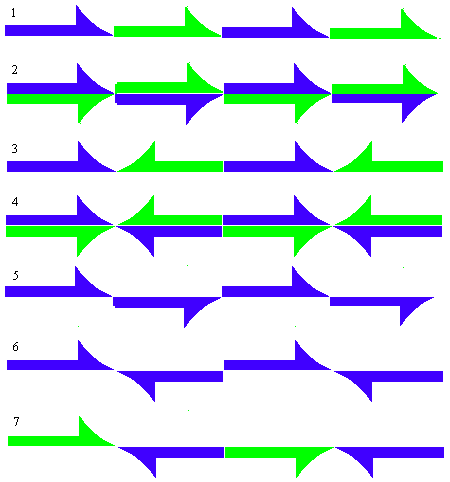
Note: Possible patterns such as:
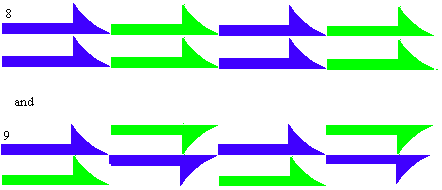
have the same symmetry as one of the 7 listed. For instance 8 = 1 and 9 = 5.

