This unit explores fractions as an extension of the whole number system. Students learn the meaning of the numerator (top number) and denominator (bottom number) in fractions symbols. They also learn to express equal shares as fractions and to order related fractions.
- Partition circles and lengths into equal parts and name the parts using fractions.
- Write fractions in words and symbols.
- Give the meaning of the numerator and denominator in a fraction.
- Order fractions that have the same numerator or the same denominator.
- Create a number line to show a set of related fractions.
Fractions arise from the need to divide. That division may involve equal sharing or measuring. Many equal sharing situations can be solved without needing fractions. For example, 1/3 of 15 or 15 ÷ 3 can be accomplished by putting five objects in each of the three shares. However, other equal divisions of sets and objects require partitioning ones, e.g. 1/3 of 16 or 1/3 of a pie. Measurements in which the units do not fit into a space a whole number of times demand the use of fractions of that unit. For example, if a length of 13 cubes is measured with a unit of 4 cubes, 13 ÷ 4 = 3 ¼ units fit.
In this unit students learn about fractions as numbers which is a measurement idea. ‘Fractions as measures’ is arguably the most important of the five sub-constructs of rational number (Kieren, 1994) since it identifies fractions as numbers, and is the basis of the number line.
Fractions are symbols in two parts, the numerator and denominator (Lamon, 2007). In the fraction 3/4, three is the numerator and 4 is the denominator. The numerator, 3, is the number of parts being counted, and the denominator, 4, gives the size of those parts. Quarters are of a size that four of them make one (whole).
Describing the relationship between different lengths might involve whole numbers, e.g. twice as long, but also involve fractions, e.g. half as long. Fractions express an amount that is in reference to a whole. With measurement that whole, or one, is fixed. For example, consider the relationship between the brown and orange Cuisenaire rods. If the orange rod is defined as one (an arbitrary decision) then what number is assigned to the brown rod?

Some equal partitioning of the one is needed to create unit fractions with one as the numerator. For the size of the brown rod to be named accurately those unit fractions need to fit into it exactly. We could choose to divide the orange rod into tenths (white rods) or fifths (red rods), either would work. By aligning the unit fractions, we can see that the brown rod is eight tenths or four fifths of the orange rod.
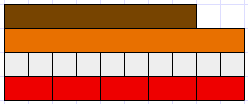
Note that eight tenths and four fifths are equivalent fractions, and the equality can be written as 8/10 = 4/5. These fractions are different names for the same quantity and share the same point on a number line. The idea that any given point on the number line has an infinite number of fraction names, is a significant change from what occurs with whole numbers.
This unit can be differentiated by varying the scaffolding provided and altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- Support students thinking by clearly and deliberately modelling how to partition a whole into equal parts, and the result of the partitioning.
- Support students to describe the process of partitioning and their understanding of equal parts in their own words. Introduce mathematical terms naturally, alongside students explanations (whole, equal parts, fractional names such as one half and one third).
- Use the terms “numerator” and “denominator” once the underlying ideas are understood, and can be articulated in students’ own words.
- Help students to record their working with diagrams, and equations, to ease demands on working memory.
Tasks can be varied in many ways including:
- easing the calculation demands by choosing fractions and sets that are manageable
- using collaborative grouping so students can support others
- reducing the demands for a product, e.g. less calculations and words.
The context of equal shares can be adapted to recognise diversity and student interests to encourage engagement. Support students to identify and explore other situations in their lives where equal sharing occurs. For example, sharing kai at home or sharing cards to play a game (the pack of cards represents one whole). Art and design often provide situations where shapes need to be equally partitioned.
Note that most of the fractions in these teachers’ notes are displayed as typed text, meaning that the vinculum (the line between the numerator and the denominator) is diagonal rather than horizontal. When writing fractions for students it is recommended that you use a horizontal vinculum.
Session 1
In this session students learn to equally partition lengths and name the parts they create as fractions. Use Copymaster One to make a set of laminated pizza pieces. Three of each page is sufficient to make a useful whole class set.
- Sit the class in a circle. Choose four students to receive a piece of pizza. The pieces must be different fractions (half, quarter, third, fifth) and placed behind the students. Ensure that nobody can see the pieces.
I gave each person one piece of pizza. That seems fair. Is it?
Students might raise the possibility that the pieces are not the same size (Different size pizzas to start, different parts).
Good point. I want everyone who got piece to have a feel of it, without looking.
How big is the piece you got? - Ask students to describe the piece they have. Look for some reference to fractions.
Can you draw in the air how big the whole pizza was?
Everyone seems to have a different sized piece of pizza.
Predict who has the most pizza? Predict who has the least?
Why are their pieces larger/smaller? - Ask the students to reveal their pizza pieces. Organise the pieces in order of size at the front. Discuss how to name the size of the pieces and how students know that it the correct fraction. Record the fractions using words, e.g. “one third” and symbols, e.g. 1/3 onto cards below the pizza pieces.
What does the 2 mean in 1/2? (This means that two of these pieces make one (whole))
Generalise the meaning of the denominator by discussing all the fractions on display. - Hold up a piece and give students practice writing the numbers and words. Develop connections between the piece, word (written and said), and symbol. Note that fraction words in English give little information about the number of parts, e.g. half means ‘twoth’ and third means ‘threeth’.
- Provide students with Copymaster Two to work through. Roam the room to support students who need more support. Look for:
- When partitioning the pizzas do students create the correct number of approximately equal parts and ‘exhaust’ the whole pizza? (Exhaust means use it all up).
- Can students record the words and symbols for unit fractions? (Unit fractions have a numerator of one)
- Can students recreate the whole pizza when given only a part and use that whole to establish the size of the part?
- Do students accept the generalisation that the more equal parts a whole is divided into, the smaller those parts are?
- Organise the fraction symbol cards on the floor in order of size (smaller to the left), i.e. 1/5, 1/4, 1/3, 1/2.
Which fraction is the largest? Which fraction is the smallest?
I am confused. Can you help me. Four is larger than three but one quarter is less then one third. Why is that true?
Students should explain that the four means more parts than the three. Therefore, the quarter parts are smaller than the thirds. - Introduce cards for 1/6 and 1/10.
Where would you put these fractions? Why?
Session Two
In this session students learn to iterate unit fractions to form non-unit fractions, like three quarters and two thirds. They also learn to order fractions with the same denominator, like one quarter, two quarters, three quarters, and four quarters.
- Begin the lesson with the class in a circle, in the same way as you started the last lesson. Instead of giving some students one piece of pizza, use halves and give four students one half, two halves, three halves, and four halves, respectively. Again, ensure the pieces are not visible to any students.
This time I gave each person a different number of pieces of pizza. In your whānau that happens because some people are hungrier than others.
Please reach behind you and count how many pieces of pizza you have. - After each student has told their number of pieces:
Who has the most pizza?
Students might think the question is trivial, but some may realise that the size of pieces matters, as well as the number of pieces. Having more pieces results in a greater amount only if the pieces the same size. - Ask each student to reveal the amount of pizza they have by arranging the pieces at the front of the class. Record the total amount they have as both words, e.g. three halves, and symbols, e.g. 3/2. Creating improper fractions (numerator greater than the denominator) helps students to recognise the role of both numbers in determining the size of a fraction.
How else could we write two halves? …three halves? …four halves? (1, 1 1/2 , 2).
What does the top number, the numerator, of a fraction tell you?
What does the bottom number, the denominator, tell you? - Ask your students to name the fraction for other amounts of pizza you make, using the pizza pieces (Copymaster One). Ensure the fractions are non-unit and some fractions are improper. Good examples might be:
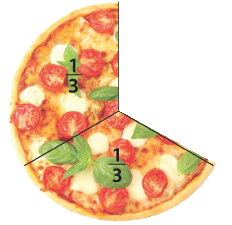
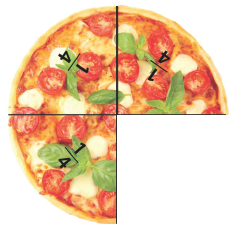
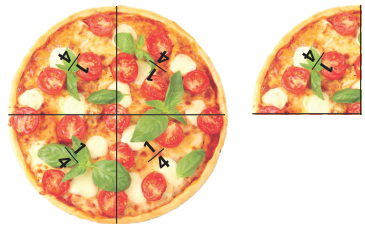

You might also invite students to make or draw given fractions. Asking students to anticipate the side of the amount before it is made is important to their development of imaging, and possibly number properties. High achievers might notice that dividing numerator by denominator gives the number of ones (whole pizzas) that can be made, e.g. 9/3 = 3 found by 9 ÷ 3 = 3. - Use Copymaster Three to provide students with copies of fraction circle pieces. Two or three of each circle is enough per student (you might reduce the Copymaster to have four circles on each A4 page). If made from card and laminated the sets last many years.
- Play Make Two in pairs, or threes.
You need: As many sets of fraction circle pieces as possible. Remove the fifths and tenths.
A set of fraction cards made from Copymaster Four.
To Play:- Play in pairs, threes, or fours. Organise the fraction pieces in collections of the same fraction, e.g. All the thirds in one place. Shuffle the cards and deal three cards to each player. The rest of the deck is placed in the middle, face down.
- Players take turns to:
- Choose one of their cards and build that fraction with pieces.
- Take the top card from the deck so they have three cards again.
- Each time a player makes a fraction, they can add it to an existing fraction, or start a new collection of parts. The aim is to make two whole circles. Players may have several partially complete double circles ‘on the go’ as they take turns.
- When a player makes two whole circles, they earn a point. The pieces are returned to the pool so they can be used again.
- The player with the most points wins, if that matters.
- Gather the class and discuss what students learned from playing the game. Points to bring out include:
- Two can be expressed using many different fractions, like 4/2, 6/3, 8/4.
- Non-unit fractions are made up of collections of unit fractions, like 5/8 is composed of five units of one eighth.
- Some fractions represent the same amount, like 3/4 = 6/8 = 9/12. These fractions are said to be equivalent.
- Let students work in threes with their fraction circle pieces and the fraction cards from the game. Here is the challenge:
Put these fractions in the correct order of size, smallest to greatest.
3/8, 7/8, 2/8, 8/8, 1/8, 4/8, 5/8, 6/8, 9/8
There are cards for all fractions but nine eighths. Students might use cards to order the fractions, confirming with circle pieces if necessary. - Ask students to order other sets of fractions with the same denominators, for example: 3/3, 5/3, 4/3, 3/3, 2/3, 1/3
- Generalise how to order a set of fractions with the same denominators.
Why is it easy to order fractions with the same denominator?
Students should note that since the parts are always the same size, the size of the fraction depends on the numerator. The more parts there are, the bigger the fraction is. - Let students work in threes on the challenge problems below. They will need fraction circles and fraction cards.
Find all the equivalent fractions in the set of cards. Write what you find as equations, like 8/12 = 2/3.Expect students to be systematic in the way they find equivalent fractions.
How can we be sure we have found all the equivalent fractions?
One approach might be to start with fractions involving halves, e.g. 1/2 = 2/4 = 3/6 = 4/8 = 6/12 and 2/2 = 3/3 = 4/4 = 6/6 = 8/8 = 12/12. Eliminate all the cards involved. Move to thirds, then quarters, then sixths, etc. eliminating cards each time.Extension:
Look at the ‘non-equivalent’ cards that are left (1/8, 3/8, 5/8, 7/8, 1/12, 5/12, 7/12, 11/12).
Why was it hard to find equivalent fractions for these fractions?
What fractions, that are not in the cards, would be equivalent to these fractions?
Extra hard challenge:
Find some fractions in your cards that are different by one twelfth.
How many can you find?
There are several pairs of fractions that have a difference of one twelfth, including one third and one quarter, five twelfths and one half, two thirds and three quarters, two thirds and seven twelfths or nine twelfths.
Session Three
In this session students use their sets of fraction circles to compare fractions. They learn to distinguish easy comparison situations (same denominators or same numerators) from more difficult situations where both numerators and denominators are different.
- Create sets of cards labelled as follows; “Greater than”, “Less than”, “Equals”, “>”, “<”, “=”. Read each card and pair up the word cards with the symbols, e.g. Greater than with >.
- Take a set of fraction cards used the previous day (Copymaster Four). Take out thirds, sixths, and twelfths cards, leaving only halves, quarters, and eighths.
Shuffle the cards and get two students to choose a card. Place the card side by side, leaving a gap for the sign.
Which sign should I put between these two fractions? - Make the two fractions to confirm the size relationship.
- Swap the fractions around and ask what signs apply then.
Do students recognise that the opposite sign applies? - Order several pairs of fractions, making the fractions if necessary, and trading the equalities and inequalities, e.g. “five eighths are greater than one half” or “Four eighths equals one half.”
- Ask students to solve the ordering problems on Copymaster Five, in pairs or threes. Most students will need access to the circle fraction pieces they used in the previous lesson. However, encourage students to anticipate the size relationship first before making the fractions.
Roam the room as students work. Look for:- Can students correctly make and draw the two fractions?
- Can students select the correct relationship sign?
- Do students recognise when the numerators or denominators are equal?
- Do students recognise when two fractions are equivalent?
- Can students anticipate the relationship between fractions with out needing to make circle models?
- Gather the class after a suitable time. Share answers looking for students to justify their thinking on a few examples.
Which fractions were easiest to compare? Why?
Which fractions were the hardest to compare? Why? - Use the same fraction cards and circle pieces from the previous tasks. Ask students to play Fraction Top Dog in threes.
To Play:- Shuffle the cards and deal five cards to each player.
- Take turns to:
- One player is the caller and calls either, “Greatest” or “Smallest”.
- The other two players lay down one card each. The player whose card matches the call wins a point. For example, if the call was “Smaller” then 25 beats 23.
- Any disputes are resolved by making the fractions with circle pieces.
- The players take the top card from the pack to replenish their five cards for next turn.
- Remember to change the caller each turn. If the fractions are equivalent neither player earns a point.
- At the end of the game when the deck is all used up the player with most points is the winner.
Session Four
In this session students transfer their learning with a circular regions model to develop a length model of fractions. The length model allows them to create a mental number line for simple fractions, and to realise fractions as an extension of the natural number system.
- Start the lesson with a reminder about the composition of non-unit fractions and how to order fractions. At level two students should be able to order fractions with the same denominator or numerator.
- Using fraction cards and circle pieces ask students to order these sets of fractions:
- 2/3 2/4 2/8
- 3/6 5/6 1/6
- 9/12 3/4 6/8 (Extension)
- Discuss strategies for ordering with a focus on the meaning of the numerator as a count, and denominator as defining the size of the parts.
- For the next two lessons students will need sets of Cuisenaire Rods. An alternative to the physical material is use a virtual version online. There are many sites that have a Cuisenaire Rod sandpit (Search: Cuisenaire rod virtual environment).
- Use PowerPoint One to drive the lesson with the whole class, with mouse clicks to animate the graphics, as follows:
- Slide One: Expect students to deduce the size of rods from the information. Avoid using a ruler to measure the actual rods as this can create pre-determine students assigning of values to the rods. Demand justification for the value assigned to each rod. You might use think, pair, share to encourage participation. Answers are (assuming dark green equals one).
- Light green rod - one half (1/2)
- Blue rod - One and one half (1 1/2 or 3/2)
- Red rod - one third (1/3)
- Brown rod – One and one third (1 1/3 or 4/3)
- White rod - one sixth (16)
- Yellow rod – five sixths (5/6)
- Slide Two
Look for students to use iteration, or repeated copying end on end. That is, take the named rod as a unit and see how many times it fits into one whole.- Yellow rod - one half (1/2)
- Red rod - one fifth (1/5)
- White rod - one tenth (1/10)
- Light green rod - three tenths (3/10)
- Dark green rod - six tenths (6/10) or three fifths (3/5)
- Crimson rod - four tenths (4/10) or two fifths (2/5)
- Slide Three
The aim of this slide is for students to use equal partitioning (equi-partitioning) to establish crimson as one half, red as one quarter, and white as one eighth. The yellow rod is five iterations of the white rod so it must be five eighths. - Provide students with Copymaster Six which contains Cuisenaire Rod challenges. If possible, let your students use physical sets of the rods. However, digital tools will also work. Roam the room as students work. Look for:
- Can students equally partition the whole, then find a rod to match the fraction?
- Do they recognise that when given a non-unit fraction they need to find the unit fraction first?
- Do they recognise that if the given rod is more than one then the whole must be smaller than that rod?
- Can they establish the whole when given a fraction part, including fractions greater than one where the whole is smaller?
- Gather the class after an appropriate time to share answers and attend to the issues above. Expect students to justify the answers. For example, “If the crimson rod equals two thirds then another third will make one whole. The third must be the red rod because two of red makes crimson. Three reds are the same as one dark green. That must be the whole.” Support the discussion using online Cuisenaire Rod tools.
Session Five
In this session the representation of a number line for fractions is developed.
- Use PowerPoint Two to introduce how to create a fraction number line. Mouse clicks allow you to animate the slides and pause where you want.
Expect your students to anticipate where fractions will be before showing the next slide. Ask them to justify why they think fractions are where they suggest. Look for the two processes of iteration (repeated copying) and equal partitioning. Make explicit that the marks on a number line, just like a ruler, are at the end of the unit.
Discuss:
Suppose I ask you to make a number line showing only halves and fifths.
Which colour would be a good rod to choose for one whole? Why?
Orange is an ideal choice because one half is the yellow rod and one fifth is the red rod. - Write these numbers on the whiteboard:
0, 1, 2, 3, 4, 1/2, 1/5, 3/2, 4/5, 6/2, 9/5 - Using the orange rod as one whole create a number line showing these fractions in their correct position. Students might work with physical or virtual Cuisenaire Rods. Roam as they work to support students with enabling prompts such as:
Tell me about the fraction you are trying to place.
What does the denominator mean?
If orange is one, which rod is one [denominator]th?
How many of that unit fraction do you need to put together?
What number in the fraction symbol tells you that?
Think about where the fraction will go before you make it with rods.
How close can you get? - Gather the class. Share the location of fractions on the number line.
If the orange rod is one, the yellow rod is one half, and the rod is one fifth, what fraction is one white rod? (one tenth)
Here are some fractions using tenths. Work with a partner to decide where on your number line these fractions will go.
5/10, 20/10, 8/10, 12/10, 3/10, 25/10
Provide Cuisenaire rods only if students need support to locate the fractions. Expect them to reason where the fractions are, to recognise equivalence, and when a fraction shares the same position as another fraction on the line. For example, 8/10 = 4/5. - Provide this independent challenge.
Use the dark green rod as one whole.
Make a number line with 0, 1, 2, 3, 4, and 5 on it using the rods.
Put as many fractions as you can on your number line.
How many fractions can you place without using other rods?
Look for students to locate halves, thirds, and sixths on their line. Some may go outside what it possible with the rods to include other fractions such as quarters, eighths, and twelfths. - Revisit the tasks in this unit. Students will enjoy playing the games again, and trying new challenges with the fraction circles, e.g. How many ways is it possible to make one half with the pieces?
Use the fraction cards for students to practice making and ordering fractions with, or without, the support of materials.
Dear family and whānau,
This week we learned about fractions as numbers. We explored the meaning of the top and bottom numbers in a fraction. Ask your child about the meaning of the numbers in a fraction like three quarters, or seven eighths.
We used two types of material to explore fractions, circles, and rods. Challenge your child to divide circles up into equal parts and to draw a number line showing the size of fractions.