This unit explores the beginnings of proportional thinking by introducing fractions and associated language. The purpose for this unit is to make, name, and recognise wholes, halves, third parts, fourth parts and fifth parts of a variety of objects.
- count in fractions forwards and backwards to a named whole number.
- recognise the whole of an object, part of an object, and equal parts and their names.
This unit is based on the work of Richard Skemp. His ideas for teaching fractions can be used successfully with year 2 students, and also with students up to year 8 who are having difficulty understanding fractions. Skemp’s use of the word ‘parts’ is deliberate in that he uses it to refer to ‘equal parts’ whereas 'bits' refers to non-equal parts.
The use of two different physical representations, the whole and parts of a whole, are used to develop the concept of a fraction. Language also plays an important role. Being able to count in fractions helps students understand that you can have 5 thirds or 6 halves.
Using denominators that are the same, students need to know:
- a whole can be divided (partitioned) into equal parts, e.g. one whole is equal to two half parts or 1 = 1/2 + 1/2
- each of those parts can be put back together to make a whole, e.g. two half parts is equal to one whole or 1/2 + 1/2 = 1
- parts can be joined to make a fraction less than 1, e.g. one fourth and one fourth and one fourth is equal to three fourths or 1/4 + 1/4 + 1/4 = 3/4
- parts can be joined to make a number more than 1, e.g. three fourths (quarters) and one fourth and one fourth is equal to one whole and one fourth or 3/4 + 1/4 + 1/4 = 1 1/4
This unit can be differentiated by varying the scaffolding provided and altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- Support students thinking by clearly and deliberately modelling how to partition a whole into equal parts, and the result of the partitioning.
- Support students to describe the process of partitioning and their understanding of equal parts in their own words. Introduce mathematical terms naturally, alongside students' explanations (whole, equal parts, fractional names such as one half and one third).
- Use the terms “numerator” and “denominator” only once the underlying ideas are understood, and can be articulated in students’ own words.
- Provide additional experiences of physically partitioning materials and discussing the resultant parts, until students understand the underlying ideas.
The context of equal shares can be adapted to recognise diversity and student interests to encourage engagement. Support students to identify and explore other situations in their lives where equal sharing occurs. For example, sharing kai at home or sharing cards to play a game (the pack of cards represents one whole). Rēwena bread modelled out of playdough could be used as another context for eels.
- Plastic knives
- Cutting boards
- Five set loops
- 3 sets of animals (these could be models or pictures)
- Five trays or plates
- Playdough recipe
- Copymaster 1: Start, action, result boards 1
- Copymaster 2: Start, action, result boards 2
- Copymaster 3: Parts cards
- Copymaster 4: Set names
- Copymaster 5: Menu for each set (on separate cards)
- Copymaster 6: Template for foods
- Copymaster 7: Think board template
- Copymaster 8: Think board for 3/5
Prior Experiences
- Idea of fair shares
- Know 1/2, 1/3 and 1/4 of shapes such as rectangles and circles
- Doubles and their corresponding halves
Although the unit is planned around 5 sessions it can be extended over a longer period of time.
Session 1
The purpose of this session is to develop students' understanding of equal parts (the denominator).
Resources:
- Copymaster 1
- Playdough (see recipe)
- Plastic knives
- Cutting boards
- Ask the students how they would share a bale of hay (block of chocolate) between 4 sheep (4 people) fairly. Other contexts could be the sharing of pizzas but the shape of the rectangle is easier for students to cut into equal shapes. Introduce the word equal – what do you think it means?
- Distribute copies of the eels start, action, results boards (Copymaster 1), some playdough, a cutting board and a plastic knife each. If it is possible it would be better to have 1 board between 2 students.
- Have each student or pair of students make six equal sized round eels, by rolling 6 equal amounts of play dough. Put one eel in each of the outlines on the left hand side of the board. The eels are small as they have their heads and tails cut off. The eels we are making today are miniatures of the big eels. That means we are making small copies of the big ones.
- The following story can be used to guide students through the actions as described on the board. The story could be adapted to a different context, such as the sharing of rēwena bread, to suit your students.
Hoepo and his brothers and sisters are at their Poua’s tangi and although they are sad they are looking forward to the hakari because shortfin eel is always on the menu.
Hoepo is planning to go early to the marquee because he wants one eel all to himself. He is given one whole eel. Hoepo doesn’t know it but he is going to be one sick boy!
The twins appear and they are told they have to share one eel evenly between the two of them. There are now two half parts.
The triplets come next and Aunty Wai says we will have to cut another eel into three equal parts. There are now three third parts.
Hoepo’s sister has come with her three friends. Aunty Wai says that they will have to cut the eel into four equal parts. There are now four fourth parts. Aunty Wai says they are also known as quarters.
Hoepo’s five baby cousins are only allowed to eat small portions so Aunty Wai cuts the last eel into five equal parts. There are now five fifth parts.
- Ask the students to mark the lines and cut lightly then if they haven’t made equal parts they can smooth the playdough out and start again.
- After cutting, the separated parts are put in the RESULT column next to their descriptions.
- Ask the students to share with the person next to them what they can see. Hopefully someone may say, "The more cuts we made, the smaller the equal part." Prompt them towards that knowledge.
I want you to look at one of the third parts and one of the fifth parts. Which is bigger?
Have the students take one of each of the equal parts and put them on another blank board.
Order the equal parts from smallest to biggest.
Let’s say the names.
Students should order from 1/5 – 1
Put them back on the original board.
How many halves are equal to the whole?
How many fourths are equal to the whole?
How many thirds are equal to a whole?
How many wholes are equal to a whole?
Depending on the age of the students symbolic notation can be introduced, using the terms like 1/2 and one half part interchangeably.
- Repeat the steps above using the biscuits start, action, results boards and fresh playdough. The first boards should, if possible, remain on view. With this second board a variety of division lines are easily found, eg fourth parts. Rēwena bread could be used as another context instead of biscuits or pies (as in number 9).

- Repeat the steps above using the pies start, action, results boards. If possible, fresh play dough should be used, the other two boards remaining on view. The lines of division should be radial as shown below.
Session 2
The purpose of this session is to develop the idea that parts of the same kind may not look alike. In Activity 1 this arose from the use of different objects. Here we see that this can be so, even with the same object.
Resources:
- Copymaster 2
- Playdough
- Plastic knives
- Cutting boards
Revise knowledge about equal parts.
What can we remember from yesterday? Write students’ comments in your modeling book.
- Begin with the first page. This is used in the same way as the board for Activity 1. Ask students to complete the first 3 lines (making halves in three different ways). There are three simple ways, see if you can find them.
The three straightforward ways are:
- Next, they complete the next two lines (the third parts) which offers only two straightforward ways.
- Complete the second page (the fourth-parts). There are six ways of doing this which are fairly easy to find.
- Students may want to go back to the halves, thirds or fourths/quarters boards and see if they can find some more.
Session 3
The purpose of this session is to consolidate the concepts formed in Sessions 1 and 2, moving onto a pictorial representation.
Resources:
- Begin by looking at some of the parts cards from Copymaster 3 together. Explain that these represent the objects which they made from playdough in the last activity, eels, chocolate bars, biscuits and some new ones. They also represent the parts into which the objects have been cut, e.g. third-parts, fourth-parts, halves, fifth-parts. Some have not been cut: these are wholes.
- Shuffle the parts cards and spread them out on the table, face upwards.
- Give each student one of the set names from Copymaster 4.
- Each student should collect the parts cards that match the name of the set they have been given, for example, halves.
- Students check each other’s sets and discuss if necessary.
- Next, introduce Skemp’s mix and match game. This is a great game in that the students are consolidating what they know about denominator without being introduced to the word. Older students may have heard that word and it is important that they understand what it is. The denominator names the number of equal parts.
Mix and Match: Rules of the Game
This game is best played by groups of 2-4 people (a tuakana/teina model could be used here).
- Share the parts cards from Copymaster 3 evenly between all players. Each player should have their cards in front of them in a single pile, face down.
- Place the mix and match card somewhere where all players can see it. The purpose of the mix and match card is to remind players of the directions in which they can build.
- The first player turns over their top card and places it in the middle of the playing area.
- Players take it in turns to turn over a card and place it alongside a card already on the playing area. When placing cards they must ensure that:
- cards in a line in the ‘match’ direction are each split into the same number of parts (e.g. halves, thirds…).
- cards in a line in the ‘mix’ direction are each split into different numbers of parts
- If a player cannot place their card they put it back on the bottom of their pile and it is the next player’s turn.
- To make the game into a contest you can give a point to any player that makes ‘three in a row’ in either direction, and add a rule that says you can not have more than three cards in a row at any time. It is possible to gain 2 points by completing both a match and a mix by placing your card in the right place. The player with the most points wins.
Session 4
The purpose of this session is to develop students' understanding of a number of like parts (the numerator).
This is the next step towards the concept of a fraction. It is much more straightforward than that of session 1 -3 which involved (i) separating a single object into part objects (ii) of a given number (iii) all of the same amount. Here we only have to put together a given number of these parts and to recognise and name the combination.
Resources:
- 3 sets of animals (these could be models or pictures)
- Copymaster 5
- Copymaster 6
- Five trays or plates
- Playdough
- Plastic knives
- Cutting boards
- Five set loops
Warm up
- Count in halves up to a number such as 3.
1/2, 2/2, 3/2, 4/2, 5/2, 6/2 (be prepared for students to carry on counting and not realise that 6/2 is equal to 3).
- Ask the students:
How many halves did we count (six halves = three wholes, write on the board)
How many halves do you think would equal 6? Write on the board
How many halves do you think would equal 9? Write on the board
- Relate back to their knowledge of doubles and halves.
A Number of Like Parts
This is an activity for up to six students working in two teams (mahi tahi). Its purpose is to introduce the concept described above.
Set the scene for your students:
Yesterday we went to the zoo and saw the zoo keepers feeding some of the animals. We are going to pretend that some of us are the animal keepers feeding the animals and some of us are the zoo kitchen staff, preparing and cutting up all the food.
- One team acts as animal keepers, the other works in the zoo kitchen. The latter need to be more numerous, since there is more work for them to do.
- A set of animals is chosen. Suppose that this is set 1. The kitchen staff look at the menu and set to work preparing eels, as in Making Equal parts. The animal keepers put the animals in their separate enclosures. They may choose how many of each. For example:
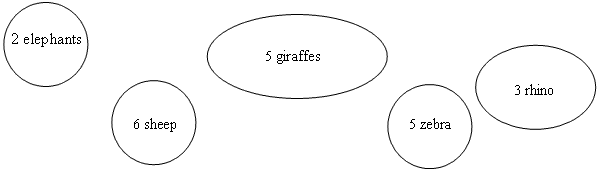
The animal keepers, one at a time, come to the kitchen and ask for food for each kind of animal in turn. The kitchen staff cut the hay as required (using the shaped playdough, plastic knives and cutting boards), e.g.
Animal Keepers may say: Zoo Kitchen Staff may say: Food for 2 elephants please Here it is, 2 whole bales of hay. Food for 5 giraffes please 5 third parts. Tell them not to leave any scraps. Food for 3 rhino please Here you are. 3 half parts from 2 bales of hay. There is one half part left. Food for 5 zebra please Here you are, 5 quarters or 5 fourth parts. Food for 6 sheep please 6 fifth parts. Lucky sheep. - Each time the animal keeper checks that the amounts are correct, and then gives its ration to each animal. The keepers check each other’s work.
- When feeding time is over, the food is returned to the kitchen for reprocessing. Steps 1 to 4 are then repeated with different animals, keepers and kitchen staff.
Note that the eels, slabs, and hay should be of a standard size.
Note also that the eels, after their head and tails are removed, resemble the eels in a cylinder shape and the slabs of meat and hay are oblongs.
Session 5
So far we have covered denominator and numerator without mentioning their names. Students need to understand that the denominator names the equal parts and numerator names the number of like parts.
Resources:
Revise some of the ideas from sessions 1-4, selecting from these activities:
- You may want to give them some unit fraction cards and ask them to order from smallest to biggest.
- Give simple fraction addition problems to add below 1.
- Give them a piece of paper and ask them to fold the paper into equal parts that they have chosen. For example, a student may choose to fold the paper into 4 equal parts. They need to verbalise what they have done. Ask them to tell you about three of the sections.
- An activity for students if the symbolic notation has been introduced could be to have a pack of cards which they can use to match pairs, e.g. 1/4 goes with one fourth. When they have matched the cards, ask each student to solve a simple addition problem for you.
I want you to give me one fourth + one fourth (write on the board). Can anyone give me cards that mean the same but are written in a different way? (1/4 + 1/4)
I want you to find one fifth and one fifth and one fifth. How many fifths are there? Can anyone give me cards that mean the same but are written in a different way? (1/5 + 1/5 + 1/5) - Give the students three problems to solve with a partner (tuakana-teina model could be used).
What happens if we had to feed 5 giraffes and they were allowed 1/3 of a bale of hay each?
What happens if we had to feed 5 rhinos and they are allowed 1/2 a bale of hay each?
What happens if we had to feed 6 zebras and they are allowed 1/4 of a bale of hay each?
To conclude the session, ask the students to work in pairs and complete a think board (Copymaster 7 provides a blank think board and Copymaster 8 shows a completed example.) Suitable fractions for think boards include 2 halves, 3 fourth parts, 2 fifth parts, 4 third parts, 2 quarters. Show and discuss the example of a completed think board for 3/5.
Dear family and whānau,
This week we have been learning about dividing things into equal parts so people get fair shares. Please draw your child's attention to any fractions you use over the week in cooking or when sharing kai or meals. For example if you are having pizza, show them how it is sliced into 4 or 6 or 8 equal sliced parts. Ask them to help share out food when dishing up dinner or making lunches. They can draw pictures or take photos of the things you talk about and bring these to class to share.
