This is a level 2 algebra activity from the Figure It Out series. It relates to Stage 5 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (389 KB)
using pictures explore the idea of equality in equations
Number Framework Links
Use this activity to help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in all domains.
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book Two, Finding a Balance, page 17
A classmate
The concept that an equation is a statement of balance or equality is vital to the development of algebraic thinking. Inequalities, shown by “more than” or “less than” situations, need to be adjusted to become equations. Helping students to come up with strategies to create equations from unbalanced situations is the purpose of this activity.
Question 2 extends the rebalancing concept by adding an “if … then” situation, which is the basis for using logical substitution strategies.
To introduce the activity, use materials like bucket balances and marbles or bolts to model the situations represented by the diagrams. For question 1a, the buckets would hold 8 and 3 respectively, and the balance arm would dip towards the 8 and show an unbalanced situation. (Make sure that the marbles or bolts have the same mass.)
The key imaging question to use here would be: How many marbles will we need to put in the righthand side to create a balance? Check the students’ responses and find the correct number. It’s important that you record this as the equation 8 = 3 + 5. Make it explicit to the students that the = sign is used to represent the idea of “balances” in the statement “8 balances 3 plus 5”.
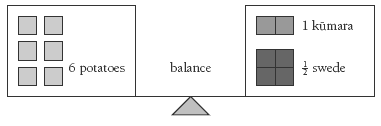
For question 2, the students will need to assume that each potato weighs the same and each kūmara weighs the same. Have the students turn each illustration into a statement or question:
“6 potatoes balance 1 kūmara and half a swede.”
“2 kūmara balances half a swede.”
“1 kūmara balances how many potatoes?”
Ask the students to make “if … then” statements to make connections between the statements, for example:
“If 2 kūmara weigh the same as half a swede, then 6 potatoes weigh the same as 3 kūmara.”
“If 6 potatoes weigh the same as 3 kūmara, then 2 potatoes weigh the same as 1 kūmara.”
A model of each vegetable can be made with multilink cubes to check out each statement. Use 1 brown cube to represent each potato. Click together 2 red cubes to represent a kūmara and 8 yellow cubes to represent a swede. If you want to confirm the situations for the students by trying the combinations shown by the illustrations in a bucket balance, you will need to use heavier materials than multilink cubes, such as the marbles or bolts suggested earlier.
Answers to Activities
Scale pictures will vary, but the equation you give for each set of scales must balance.
1. Possible equations include:
a. 8 = 3 + 5, 8 = 3 + 3 + 2, 8 = 3 + 3 + 1 + 1, and so on. On your scales, you must have 8 objects on the left-hand side and 8 objects on the right-hand side.
b. 3 = 3, 3 = 1 + 1 + 1, or 3 = 2 + 1
c. The obvious one is 15 + 8 = 15 + 8, but there are other possible answers, including:
20 + 8 = 15 + 13, 8 + 8 = 15 + 1, 9 + 8 = 15 + 2, and so on.
d. 8 + 16 = 12 + 12, 8 + 16 = 6 + 6 + 12, and so on.
2. 2 potatoes. Discussion will vary. The second scales will tell you that swede = 2 kūmara. You can put these kūmara into the first scales and take out the swede. Now the first scales say that 6 potatoes = 3 kùmara. This means that 2 potatoes will equal 1 kūmara.
3. Problems will vary.