This is a level 4 geometry strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (405 KB)
use compass bearings to describe positions
Copymaster of map
Map of your school
Protractor
Ruler
FIO, Level 4, Geometry, Book One, Find the Spot, page 20
Classmate
The ancient Babylonians believed that the year was made up of 12 moons, each lasting 30 days, which gave a total of 360 days in a year. The Babylonians are thought to have been the first serious astronomers, so they may have been the first to divide a circle into 360 degrees. 4000 years later, we still use degrees to
measure directions and angles. Aircraft, ships, and orienteers all use compass bearings in degrees to describe their direction.
Navigation is the process of finding your way on land, at sea, or in the air. Students who are involved in sailing, orienteering, or tramping or who are interested in gaining their pilot's licence will already know that navigation skills are useful and sometimes vital. The two basic tools for navigation have long been a map and a compass. At sea, a chronometer and a sextant have also been essential tools for the last 250 years.
Modern direction-finding devices that use global positioning systems (GPS) are now increasingly replacing the old methods.
Activity
In this activity, the students locate particular spots on an illustration using compass bearings. They then make up their own sets of clues, based on locations around their own school grounds.
Before setting this activity, you may find it best to specifically teach your students how to use a protractor on a map. Students often get confused by the two competing scales on a protractor and have trouble using a protractor that goes only to 180 degrees to measure angles that are greater than this. (You may like to show them a circular protractor.)
You should also emphasise the two points made in the speech bubbles: bearings are always measured clockwise from north, and they are always written as 3-digit numbers.
Question 1 is best done using back bearings, as explained in the panel. If we know the bearing of B from A, the back bearing gives us the bearing of A from B. To find the back bearing:
- add 180 degrees to the bearing if it is less than 180 degrees (for example, the back bearing of 081o is 81 + 180 = 261o )
- subtract 180 degrees from the bearing if it is greater than 180 degrees (for xample, the back bearing of 308o is 308 - 180 = 128o).
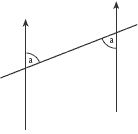
Back bearings make use of the fact that alternate angles are equal.
Alternate angles are formed whenever a line cuts across a pair of parallel lines, as in this diagram.
If the students find the back bearings from two features, this will give them two lines that cross at the spot they are trying to find. The other clue is an "extra"; your students should use it to check that they have found the correct location. Question 2a asks why distance is not needed. The reason is as above: 2 bearings always
cross at a single point unless, of course, they are the same. If only 1 bearing is given, distance also must be given to fix a location.
Before starting this activity, find out if there is a school map available. It needs to be fairly accurate and to scale if it is to be used in question 3. As an alternative, if your school has orienteering compasses, you may wish to do this task outside.
As extension activities, the students could investigate:
- the difference between true north and magnetic north
- the technologies that are used for modern navigation
- the history of navigation
- why the inventions of the chronometer and the sextant were so important.
Answers to Activity
1.
2. a. Because we are given several bearings for each spot. The bearings all cross at a common point, so we know that it is the spot we are looking for. (If we had
only 1 bearing, we would also need to know the distance if we were to find
the spot.)
b. 2
3. Practical activity. Results will vary.