Filling the Gaps

Problem One

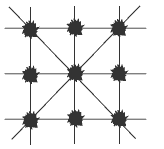
This is a reasonably difficult problem. If the students start with the arrangement shown, they are likely to extend it to:

But this gives only eight lines of three. It’s not possible to add any other straight lines that go through three trees, as the diagram below shows:

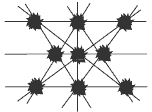
So this is obviously not the correct arrangement. However, this arrangement can be varied slightly to give 10 lines of three trees. Start with three parallel lines. Put one tree on each line so that the trees are one on top of each other:

Then put two more trees on the top line, one on either side of the existing tree and the same distance from the existing tree. Do the same on the bottom line. Make sure the trees on the bottom line are the same distance from the middle tree as the trees on the top line.

Draw as many lines as you can through three trees.
Now you have six lines, and you still have two trees left to place. Drawing lines from the middle top tree through each of the outside bottom trees and two more lines from the middle bottom tree to each of the outside top trees will give 10 lines altogether and also show where on the middle horizontal line to put the last two trees.
Place the last two trees:

Problem Two

This is a good problem for the students to discuss among themselves and compare their methods. One method is to find what a smaller common value, for example, 100 grams, is worth. Divide the price of packet A by 3 (because the volume is also divided by 3 to get 100) to get 93.33 cents per 100 grams, divide packet B by 5 to get 94 cents per 100 grams, and divide packet C by 8 to get $1.19 per 100 grams. Clearly, packet A is the cheapest per 100 grams and so is the best value.
Another method is to find a higher common value, that is, a multiple of all three volumes. The lowest common multiple is 12 kilograms or 12 000 grams. Multiply packet A by 40, packet B by 24, and packet C by 15 to find the cost of 12 kilograms of each packet and then compare the values.
Extension
Students could investigate the prices of different volumes of items at a supermarket or use an online supermarket on the Internet.
“Take three different volumes of the same item. Without calculating, which one seems the best value? Does it work out to be the best value after calculating?” The students may notice that generally, with items of the same brand, the larger the volume, the better the value. They could discuss why this is. They could also look at how some items are priced. For example, the price of fish is usually given per kilogram, but sometimes it is given per 100 grams. “Which seems cheaper: salmon at $21.40 per kilogram or salmon at $2.14 per 100 grams? Why might supermarkets decide
to price by the kilogram or per 100 grams?”

Problem Three

The students should be able to see that the difference between consecutive products increases by 2 each time. Something else that you might like to note is that the first product is 2 x 1, the second is 2 x (1 + 2), the third is 2 x (1 + 2 + 3), the fourth is 2 x (1 + 2 + 3 + 4), and so on. The difference between the second and third product will be the difference between 2 x (1 + 2) and 2 x (1 + 2 + 3), in other words, 2 x 3 = 6. Similarly, the difference between the third and fourth products is 2 x 4 = 8. The differences between the subsequent consecutive terms are 10, 12, 14, and so on.
This gives what is known as a recurrence relation between consecutive products.
Another pattern is that the final digit in the answer cycles round. It goes 2, 6, 2, 0, 0 and then round again, 2, 6, 2, 0, 0. Do the other digits follow any pattern?

Problem Four

One way to go about this is to use the hints and pick a set of numbers that adds up to 18, for example, 1 + 8 + 9. But 189 can’t be the sum because two other three-digit numbers would have to add up to 189. What about 819?
How can you get 9? Try starting with 3 + 6. Then you have to get 1 in the second place. Try 4 + 7. Actually, there’s no other way to get 11 since you’ve used up 6 (that could have gone with 5), 8 (that could have gone with 3), and 9 (that could have gone with 2). At this point, the equation is 43 + 76 = 819. The only two numbers that you haven’t used yet are 2 and 5:
243 + 576 = 819 and 543 + 276 = 819.
Once you have one answer, you can rearrange the digits to get many other answers. For example, 243 + 576 = 819 and so does 246 + 573, 276 + 543, and 273 + 546.
Why the sum of the digits in the answer is always 18 and why there is a carry-over are analysed in full on the nzmaths website: www.nzmaths.co.nz

Hints for Students

1. Experiment and work systematically. Try placing two more trees to start with.
Draw as many lines as you can. Can you see a place to put the last two trees that means there will be 10 lines?
The arrangement will have two lines of reflectional symmetry (mirror lines) that are at
right angles to each other.
2. How much would 100 grams from each packet cost?
3. How can you get the next answer from the last answer?
4. There are many answers to this problem, but in all the answers, the digits in the sum add up to 18. Remember that you will probably have to carry over digits from one column to the next. Try guess and check.

Answers to Problems

1.

2. The 300 g packet
3. a. 2, 6, 12, 20
b. 5 x 6 = 30
6 x 7 = 42
7 x 8 = 56
8 x 9 = 72
9 x 10 = 90
c. The pattern of the differences between consecutive terms is 4, 6, 8, 10, 12, and so
on. In other words, the difference between consecutive terms increases by 2 each time.
4. There are many answers, but eight possible solutions are:
314 + 658 = 972
341 + 586 = 927
134 + 658 = 792
243 + 576 = 819
735 + 246 = 981
215 + 748 = 963
271 + 593 = 864
142 + 695 = 837
(Look at the digits in the sum part of the first three answers. That should open up some other possibilities with the rest of the answers given.)