Eye Antics

Problem One

a. The students can model this problem with sticks and experiment to find the answer. If the students are having difficulties, they could try Problem One, page 3, in Problem Solving, Figure It Out, Level 3, as a warm-up.
b. To find the smallest number of sticks, you need to turn the fish around, make two drawings, one with the fish facing left and the other with them facing right. Put one drawing on top of the other. Move this drawing around until as many sticks as possible match up. Only eight sticks can be the same. There are 14 sticks altogether, so six sticks have to be moved. This shows that you can’t re-orientate the fish by moving less than six sticks.
Extension
Ask the students to find a pattern in the number of fish and the minimum number of sticks moved. What is the smallest number of sticks that they need to move to turn around three fish swimming together? How about 90 fish swimming together?

Problem Two

There are 12 squares that need to be divided into four pieces, so each piece has to have three squares. There are only two possible smaller shapes:

Four copies of shape i will not fit into the original shape, but four copies of shape ii will.

Problem Three

This problem uses the students’ knowledge of basic facts and encourages them to think about the effects of the four operations. The students will probably start with a wildcat approach to this. They’ll see what they can make without too much work and then concentrate on the more difficult ones that don’t come out quickly.
One way to be slightly more systematic is to take the numbers 1, 2, and 3 in order and then put plus and/or minus signs between them. For example:
1 + 2 + 3 = 6     1 + 2 – 3 = 0    (1 – 2) + 3 = 2
Then the same sort of thing can be done with multiplication and addition or subtraction:
(1 x 2) + 3 = 5      1 + (2 x 3) = 7
(1 + 2) x 3 = 9      (–1 + 2) x 3 = 3
After exhausting all possibilities with 1, 2, and 3 in order, students can experiment with the numbers in different orders. For example:
(1 x 3) – 2 = 1      (1 + 3) x 2 = 8
The solutions in the Answers show other possibilities with the numbers in different orders.
Extension
Can the students find ways to get numbers bigger than 9?
What numbers can the students get using 2, 3, 4? (You could send this problem home for the students to try with their families.)

Problem Four

Many of the students will probably do this using trial and improvement. This is fine to get an idea of what the problem is about. But they need to work systematically to be sure they have found all the different ways. If they use trial and error in a, encourage them to be systematic in b.
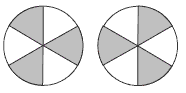
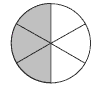
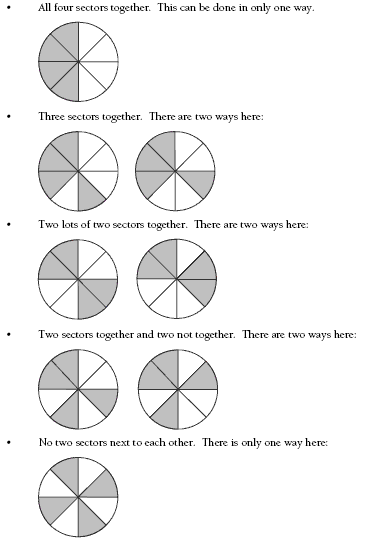
The students need to remember that some circle drawings are the same. For example, in the two shown below, you can get the second one from the first one by rotating it through 60 degrees.

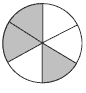
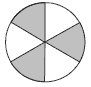
a. To get one half, three sectors need to be shaded. How many ways can this be done?

• Three sectors next to each other. This can be done only one way:

• Two sectors next to each other, with the other one separated by one or two white sectors. Again there is only one way:

• No two sectors next to each other. This can also be done only in one way:

Hence there are only three ways to shade the sectors so that they show one half.
b. For this question, four sectors make up a half. The different ways of arranging the
sectors are:

Hence there are eight ways to shade the sectors so that they show one half.
Extension
How does this problem work if you divide a square into an even number of smaller squares and shade half the squares?

Hints for Students

1. Experiment with some sticks.
How can you be sure in b that you have moved the smallest number of sticks?
2. How big are the pieces? What shape can they be?
3. Experiment and work systematically.
4. Ways that are the same as others when rotated or reflected are not counted as different ways.

Answers to Problems

1. a. One solution is:

b. 6. One solution is:

2. There is only one solution:

3. There are many ways of doing this.
Some possible expressions are:
0 = 3 – 2 – 1
1 = 1 x (3 – 2)
2 = 3 – 2 + 1
3 = 3 x (2 – 1)
4 = 3 + 2 – 1 or 2 x (3 – 1)
5 = 3 x 2 – 1 or 2 ÷ 1 + 3
6 = 1 + 2 + 3 or 3 x 2 x 1 or 3 ÷ 1 x 2
7 = 3 x 2 + 1
8 = 2 x (3 + 1)
9 = 3 x (2 + 1)
Note that some expressions can be rewritten in a different way. For example, 1 = 1 x (3 – 2) is the same as 1 = (3 – 2) x 1.
4. a. Three ways. (Ways that are the same through rotation or reflection are not
included.)
b. Eight ways. (Ways that are the same through rotation or reflection are not
included.)