This unit supports students in learning to solve a range of problems involving exponents.
- Express a power as multiplication of the base, e.g. 54 = 5 x 5 x 5 x 5.
- Recognise patterns in the last digits of powers for the same base.
- Multiply and divide powers with the same base by adding or subtracting the exponents, e.g. 24 x 23 = 27 and 27 ÷ 24 = 23.
The learning opportunities in this unit can be differentiated by providing or removing support to students, and by varying the task requirements. Ways to support students include:
- providing extended opportunities for practise of the different tasks explored in this unit
- modelling the mathematics explored in this unit (e.g. the solving of equations, construction of tables, and application of formulae)
- providing opportunities for individual, grouped, and paired work
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities (e.g. creating a graph).
This unit is focussed on using solving a range of problems involving exponents, and as such, is not set in a real world context. You may wish to explore real world applications of exponents in teaching sessions following the unit. For example, many finance and science contexts offer engaging opportunities for learning about exponents
Te reo Māori kupu such as ōrau (percent) could be introduced in this unit and used throughout other mathematical learning.
Session 1
- Show students Slide One of PowerPoint One which shows the building up of powers of two. The animation shows the first four iterations; 1, 2, 4, 8. After that control the animation with mouse clicks.
What comes next?
How do you know?
What is the same about all the numbers in the table?
- You may need to tell students that these numbers are powers of two if they do not know. Start with four, which is 22 (two squared, or two to the power of two). 22 can be written as 2 x 2. Eight is 23 and can be written as 2 x 2 x 2. Sixteen is 24 and can be written as 2 x 2 x 2 x 2.
- Slide Two repeats the animation and inserts the powers of two.
Can you predict how the pattern continues to the right and left?
Encourage students to notice that the model doubles in volume as another number is added to the right. Further mouse clicks show this.
What happens to the model as we move one place to the left?
- Slide Three shows that the volume halves, divides by two, with a move of one place to the left on the table. Students need to understand that powers of two with exponents less than two are ‘acts of imagination’ designed to fit the pattern.
The facts 21 = 2 and 20 = 1 seems counter-intuitive to some students.
What will come next on the table as we move to the left? By pattern, 2-1 comes next left and is the result of halving 1 (2-1 = ½).Therefore, 2-2 = ¼, as half of one half is one quarter.
- Let students solve the problems on Copymaster One in pairs. Look to see if your students:
- Recognise that the powers of two increase by a factor of two in the positive direction.
- Recognise that the powers of two decrease by a factor of two in the negative direction.
- Use the recurring pattern of digits in the ones place to predict further powers, e.g. the ones digits recur in the pattern 2, 4, 8, 6, … so that element of repeat can be used to know 21001 must have 2 in the ones place.
- Notice that the answer to multiplying powers of two is always in the set of powers of two.
- Notice that the answer to dividing a power of two by a power of two is always in the set of powers of two.
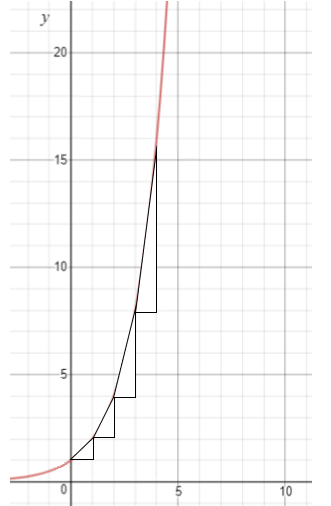
- Gather the class together to process their answers. It is enough, at this point, for students to notice the final two bullet points, without fully understanding why that occurs. Finally, ask the students to use an online graphing tool or a graphics calculator to graph y = 2x. Ask them what they notice. Focus the discussion on the slope of the graph and why it increases. For every increment of one in x, the rise (increase in y) doubles. Also notice that y = 1 when x = 0 since 20 = 1.
Session 2
In this session students compare powers of three with the powers of two they learned in the previous lesson.
- Slide One of PowerPoint Two provides graphics for the building up of powers of three using multiplication by three. Ask predictive questions:
What will happen next to the cube model?
What power will come up next?
How many cubes will that power be in total?
- Students might continue the table to the right using Copymaster Two and a calculator. You might show students how the xy button functions on their calculator as well as repeated use of multiplying by three, i.e. 1 x 3 = = = = = …
- Slide Two of PowerPoint Two works in the opposite direction, to the left, by dividing the previous term by three. Continue to ask predictive questions, especially about 31 and 30. Students should continue the pattern to the left on Copymaster Two.
- Discuss the negative powers of three. Use Slide Three of PowerPoint Two as a stimulus.
What is 3-1? How do you know?
- Taking a single cube (30) and dividing it into three equal parts gives thirds. 3-1 = 1/3.
- Taking one third of a cube and dividing it into three equal parts gives ninths. 3-2 = 1/9
The process continues infinitely to create unit fractions of the form 1/3n
- Let your students work in pairs on Copymaster Two.
Do your students see any connections between their discoveries with powers of two and the exercises they are doing with powers of three?
- After a suitable time bring your class together to compare the growth of powers of two and tree using Slide Four of PowerPoint Two.
Why do powers of three grow so much faster than powers of two?
Imagine what the graph of powers of three looks like compared to the powers of two. What do you expect?
- Ask your students to use an online graphing tool or a graphics calculator to graph y = 2x and y = 3x. Ask them what they notice. Focus the discussion on the slope of the graph and why it increases. For every increment of one in x, the rise (increase in y) doubles. Also notice that y = 1 when x = 0 since 20 = 1 and 30 = 1. Ask your students to anticipate the graphs of y = 4x and y = 1x/2 or y = 1x. Graph all four functions on the same co-ordinate plane.
What changes as the base increases?
Why is the graph of y = 1x a horizontal line? Why does y equal one for any value of x?
What do you think the graph of y = 1x/2 looks like? Graph it to find out.
Why is the value of (0.5)x deceasing as x gets greater?
Session 3
In this session students apply their knowledge of powers of two and three to solve realistic problems. The film Pay It Forward (2000) includes an interesting school project idea by the lead character, Trevor, played by Haley Joel Osment. His scheme is that he starts a chain of ‘gifting’ by doing three people a significant favour. They are asked to each do three other people a huge favour. Those nine people then provide a favour for three people each, and so on. You may want to look for the trailer to the film online and play it to your students. Consider adapting this context to reflect the names of students in your class. Perhaps this session could accompany learning around Random Acts of Kindness or your school values (e.g. manaakitanga).
Problem:
In round one, there is only Trevor. He does three people a favour. After round two there are four people, Trevor and three others, feeling good.
How many people are feeling good after … round three?...round four? … round five?
If you start Pay It Forward, how many rounds will it take before everyone in New Zealand is affected?
- Ask your students to solve the problem in pairs or threes. Allow access to computers, calculators, and materials (like cubes) if students need them. Look to see if your students:
- Recognise that for each round the increase in the number of people is a power of three
- Realise that the total number of people after each round is the sum of powers of three
- Organise their data in a table.
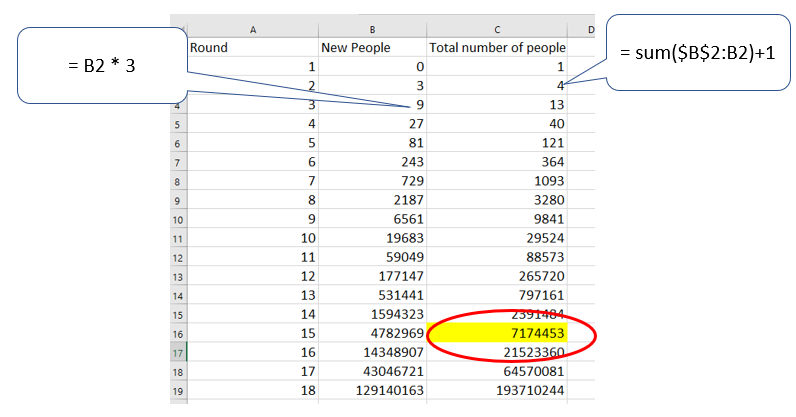
- This spreadsheet shows how computational thinking can be used to solve the problem. The formulae in cells B3 and C2 were filled down to generate the values. By round 15 over 7 million people have received a favour.
- After an appropriate time gather the class together to discuss how the students solved the problem.
How many rounds would it have taken if two people, not three, were each given a favour? (By round 23 8.38 million people have received a favour)
How many rounds would it have taken if five people, not three, were each given a favour? (By round 12 12.2 million people have received a favour)
What is the effect of changing the number of people given a favour each round?
- Copymaster Three has other problems related to powers.
Session 4
In this session students learn how to multiply and divide with powers of two, three and five using the laws of exponents.
- Work through the examples on PowerPoint Three. Slide Four summarises the results.
What do you notice about the product when two powers of three are multiplied?
Can you explain to someone else why that happens?
- Continue with PowerPoint Three to see if the relationship holds for powers of two and five.
How could we write what we have found as a rule?
You may need to remind your students that the number being repeatedly multiplied is the base and the number of that base being multiplied together is an exponent. For example, with 53, meaning 5 x 5 x 5, five is the base and three is the exponent. There are two levels of generalisation possible with the power laws.
Students might suggest something like this:
“To find the product of powers of two, add the exponents.”
Let’s use m and n to represent the exponents.
How can we write the rule? (2m x 2n = 2m+n)
A further generalisation might be prompted by asking:
Must the power have a base of two? Does the rule work with other bases?
Students might refine their statements:
“To find the product of powers with the same base, add the exponents.”
Let’s use m and n to represent the exponents and X to represent the base.
How can we write the rule? (Xm x Xn = Xm+n)
- Give your students Copymaster Four to apply multiplying powers. This requires students to discover the following ideas about powers.
- Pairs of factors for a given power can be found using the addition of exponents law, e.g. 212 = 26 x 26 = 64 x 64 = 4096. Other pairs of factors include 25 x 27, 24 x 28, 23 x 29, …, 2-2 x 214, etc.
- The square of a power is the power with the same base that has double the exponent, e.g. 26 x 26 = 212. This can be written as (26)2 = 212.
- The square root of a power is the power with the same base that has half the exponent, e.g. √ 212 = 26. This can be written as (212)1/2 = 26.
- The inverse of the multiplication law is the division law. To find the quotient of two powers subtract the exponents, e.g. 27/23 = 27-3.
Session 5
In this session students explore further applications of the power laws for multiplication and division, including a focus on negative powers.
- PowerPoint Four revisits division of powers with the same base. Ask the students to anticipate the results of calculations using the law of subtracting exponents.
- For assessment purposes ask students to complete the five examples on Copymaster Five. They should attempt these examples independently. Discuss the answers later as a whole class. Place as much emphasis on the justification of the answer as on the answer itself.
Watch Video One which is about negative powers of two. Look for students to extend this table using repeated halving:
2-42-32-22-1202122231/161/81/41/21248
If we started with 30 what would happen then?
What would happen with negative powers of five?
- Take a large place value block cube.
This is a model of 100. What is 100? (One)
To make 10-1 what do I need to do?
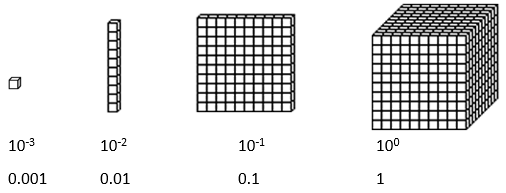
- Show that cutting a ‘one’ cube into tenths produces ‘flats.’
What should we call this block if the cube is one?
If the flat is one tenth, 10-1, it can also be named as 0.1.
What will the blocks for 10-2, and 10-3, look like?
- Equally partitioning into ten parts produces this model:
- Finish the session with this investigation.
Jess thinks that it is easy to work out a negative power if you know the positive powers with the same base.
She uses this example: - 10-410-310-210-11001011021031/100001/10001/1001/101101001000
She says "The negative power is always a fraction. One is the numerator and the denominator is the matching positive power."
What does Jess mean? Give some examples
Is she right?
How could Jess’s rule be written using a formula? - Let your students explore Jess’s rule to see if they can generalise that x-m = 1/xm. For example, 3-4 = 1/34 and 5-3 = 1/53.
Families and whānau,
This week we have been learning to solve a range of problems involving exponents. Ask your child to share their learning with you.