The purpose of this activity is to support students connecting equivalent fractions as numbers with equivalent fractions as operators. Since equivalent fractions represent the same number, the result of operating with equivalent fractions on a given whole number is the same.
- Counters, tiles or cubes, paper, and pens.
- Imagine you have 48 counters. I will give you a different fraction each time. Find that fraction of 24.
- Find three quarters of 48 counters. (3/4 x 48 = 36)
- Find six eighths of 48 counters. (6/8 x 48 = 36)
- Find nine twelfths of 48 counters. (9/12 x 48 = 36).
- Reflect on the process on finding the fractions.
What do you notice about the answers?
Why are the answers the same? (The fractions are equivalent – of the same magnitude/size)
If necessary, use a physical model to illustrate why the answers were equal.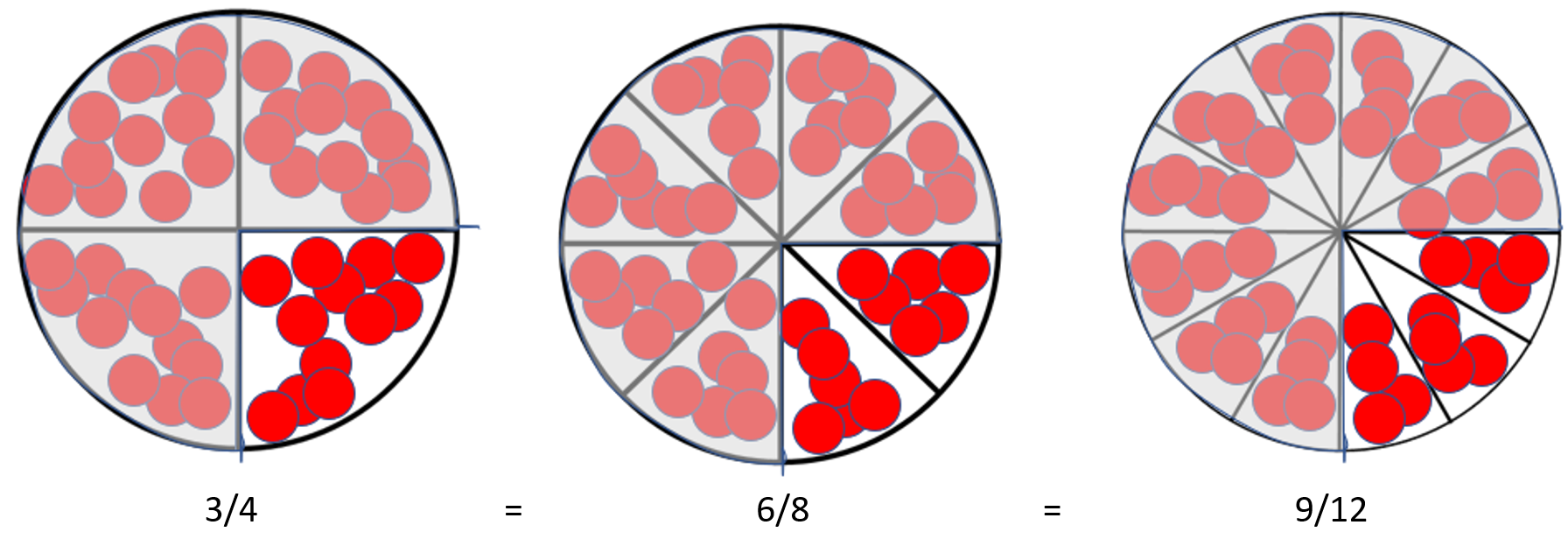
- Pose further examples, some with equivalent fraction operators, and some without. Look for students to:
- Apply a broad range of multiplication and division facts.
- Notice when operators are equivalent fractions or not.
- Anticipate the results of the calculation as either equal, less, or greater.
Good examples are shown below. Consider what groupings will be most appropriate for your students. Whilst some may benefit from tuakana-teina relationships in structured peer groups, others are likely to be ready to work independently. Some students may also benefit from further teacher support. Consider also the different means of action and expression (e.g. verbal, written, digital, physical) that your students might use to demonstrate their thinking.
- Which amount is greater, or are they equal?
Two thirds of 27. (2/3 x 27 = 18)
Six ninths of 27. (6/9 x 27 = 18) - Which amount is greater, or are they equal?
Eight tenths of 60. (8/10 x 60 = 48)
Four fifths of 60. (4/5 x 60 = 48) - Which amount is greater, or are they equal?
Three quarters of 32. (3/4 x 32 = 24)
Seven eighths of 32. (7/8 x 32 = 28) - Which amount is greater, or are they equal?
Four sixths of 42. (4/6 x 42= 28)
Two thirds of 42. (2/3 x 42 = 28)
Next steps
- Support students to use increasingly difficult multiplication and division basic facts and equivalent fractions to anticipate the result. Suitable equivalent fractions are those based on two thirds, three quarters, and three fifths.
- Encourage students to use one result to establish whether another result is greater or less. For example:
- If three quarters of 56 equals 42 (3/4 x 56 = 42), is six eighths of 56 more or less than that, or equal to it?
- If four fifths of 60 equals 48 (4/5 x 60 = 48), is eight tenths of 60 more or less than that, or equal to it?
- If three ninths of 72 equals 24 (3/9 x 72 = 24), is three sixths of 72 more or less than that, or equal to it?
- If seven eighths of 64 equals 56 (7/8 x 64 = 56), is three quarters of 56 more or less than that, or equal to it?
- Highlight fractions that are equivalent to one by posing problems such as “which is greater, six sixths of 42 or seven sevenths of 42?”