This unit of work investigates how relational thinking is applied to multiplication and division.
- Use relational thinking as a basis for a range of number strategies.
- Explain number strategies using materials and diagrams.
The equal sign signifies a balanced relationship between the numbers and operations on either side of the sign.
If the numbers on one side of the equal sign are changed, then relational changes must be made to the other side to maintain equality, e.g. seven is added to both sides.
Understanding the relationship between numbers on either side of the equal sign is fundamental in a range of operational strategies. Importantly, it is integral to the solving of increasingly complex equations in algebra.
Two progressions are implicated in students’ development to think in relational ways with multiplication and division equations.
Variables Progression
- Unknowns are treated as irreconcilable or ignored
- Unknowns are treated like specific ‘missing’ numbers
- Unknowns are treated as possibilities, that is they can take up various values
- Variables are related to other variables without needing to be evaluated
Multiplicative Progression
- Equal sets are counted or shared one item at a time
- Equal sets are counted, added or shared in composites, e.g. skip counting
- Multiplication facts are worked out (derived) from known facts, or simply known
- Properties of multiplication and place value are applied
- Multiplication is connected to division
This unit aims at phases 2-4 of the ‘Variables’ progression and 3-5 of the ‘Multiplicative’ progression.
The learning opportunities in this unit can be differentiated by providing or removing support to students, or by varying the task requirements. Ways to support students include:
- making connections between this learning, previous learning around multiplication and division, and between the counting of units in arrays
- using materials to support students who find it difficult to understand the properties of multiplication. Ultimately, students should appreciate the transformations on the quantities involved
- asking predictive questions to help students think abstractly sbout concepts rather than rely on physical representations. Symbols are extremely important in connecting different situations, and some students recognise patterns in equations more readily than in other representations.
- encouraging sharing and discussion of student's thinking
- using collaborative grouping (mahi tahi) so students can support each other, share strategies, and experience both tuakana and teina roles.
Ways to extend students include:
- encouraging students to generalise the properties of multiplication and how those properties transfer to division, the inverse operation
- identifying and describing operations that can be performed on both sides of an equation that leave the equality invariant.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. For example, you could look for arrays in the following ways and use them as contexts for multiplication and division problems:
- lining up for kapa haka performances
- apple trees growing in an orchard
- lineouts in rugby games
- muffins baking in trays
- Weet-Bix stacked in a box
Te reo Māori vocabulary terms such as whakarea (multiply, multiplication), whakawehe (divide, division), taurite (balance), paheko kōaro (inverse operation), paheko (operation), and ōrite (equal) could be introduced in this unit and used throughout other mathematical learning.
Session 1
This session explores how relational thinking applies to multiplication, with a focus on the commutative and distributive properties. When designing arrays problems consider, and encourage students to think about, contexts in which the arrays might be relevant (e.g. 5 rows of 3 kiwi eggs lined up in an incubation pod). It is also important to consider what multiplication facts will allow students to easily understand the idea of “arrays” and which multiplication facts might act as a cognitive barrier. Group students with different levels of multiplication-facts understanding to encourage tuakana-teina.
- Discuss why this multiplication equation is true, and what the relationship is between the numbers on the left of the equal sign and the right: 3 x 5 = 5 x 3. Note that some students will evaluate both expressions, 3 x 5 and 5 x 3, and conclude “both sides work out to 15”. Others may note that the factors are reversed in order (the commutative property).
- Physically model the equality of 3 x 5 and 5 x 3, by creating arrays like the one displayed below. Arrays could be created using a digital platform (e.g. Google Slides), physical materials (e.g. counters), or drawn.

Can students explain which array models 3 x 5 and why? (3 x 5 represents either three rows of five or five rows of three so either answer is justifiable)
Some students may recognise that one array is a quarter turn of the other. - Pose similar examples, such as 4 x 6 = 6 x 4 and 2 x 7 = 7 x 2. Ask students to construct a single array (using Copymaster 1) for each equation and show where the factors are found, i.e. rows or columns.
- Provide equations with unknowns in different ‘locations’, e.g. 8 x 5 = 5 x ? and 6 x ? = 3 x 6. Can students find the unknown without evaluating the given side of the equation?
- Provide Copymaster 2 to the students with minimal guidance. The worksheet provided examples of the distributive property. For example, 3 x 7 = 3 x 5 + 3 x 2. Let the students work collaboratively (mahi tahi) in small groups.
- Gather the class to share the answers. Highlight that the word ‘distribute’ means to share out. One or both factors are shared, e.g. With 3 x 7 = 3 x 5 + 3 x 2, 7 is distributed into 5 and 2.
- Give examples of the distributive property where the unknowns are in different ‘locations’, e.g. 5 x 13 = 5 x ? + 5 x 3 or 3 x ? = 3 x 6 + 3 x 6. You might construct arrays to show some equations.
Session 2
- Discuss why this multiplication equation is true, and what the relationship is between the factors on the left of the equal sign and the right: 14 x 5 = 7 x 10
- Re-arranging a 14 x 5 array to become 7 x 10 will help students to understand that nothing has been added to or taken away from the array, so there will be the same number of pūkeko. (see Copymaster 1).
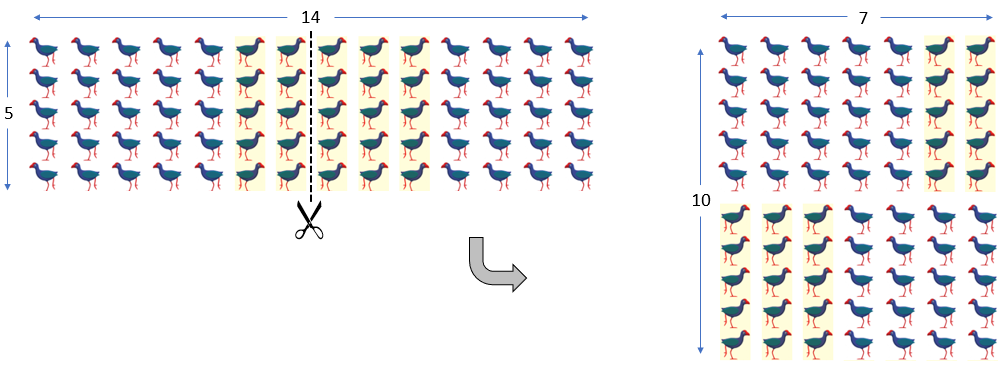
- Relate the re-arrangement of the array with the more abstract equation representation:
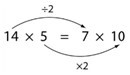
- Do your students recognise that the equality is conserved if one factor is halved while the other is doubled?
- Give students some multiplication equations like the following. Ask them to decide whether, or not, each equation is true. Do students accept the equality without working out the products on either side of the equal sign? (Bold equations are true)
8 x 5 = 4 x 10
12 x 4 = 6 x 8
14 x 3 = 6 x 6
4 x 15 = 2 x 30
18 x 50 = 8 x 100
6 x 7 = 2 x 21
- You might build arrays of each product (on opposite sides of equals). Ask how one array can be transformed into the other by cutting and pasting. Connect the cutting to halving one factor and the pasting to doubling the other factor.
- The following multiplications require students to think about the multiplicative relationship between the factors on either side of the equal sign. Frame these equations in a context that is relevant to your students. It is important to get students to explain and discuss their strategies. Ask students to use arrays to show how their strategies work, in situations where they seem uncertain.
16 x ? = 8 x 10
12 x 10 = ? x 5
? x 3 = 9 x 6
8 x ? = 4 x 12
24 x 50 = ? x 100
4 x 9 = ? x 3
- Show PowerPoint 1 to the students. Slide One shows examples of identifying a relationship between two equations. Ask your students what relationships they see among the factors in the equations. Record the pairs as equations, e.g. 6 x 4 = 3 x 8. Slide Two shows examples of equations connected by the distributive property. Trios of equations can also be combined into a single equality, e.g. 2 x 11 + 4 x 11 = 6 x 11
- Provide the students with Copymaster 3 which is a Times Tables Chart. Ask them to the find duos and trios of connected equations. Can they write each duo and trio as a single equality?
- Extension: High achieving students might extend their thinking into equations that contain variables. What values for the heart (♥) and diamond (♦) work for each equation? Note that there is an infinite set of possibilities for each equality.
4 x ♥ = 8 x ♦
♦ x 9 = ♥ x 3
12 x ♥ = ♦ x 6
♥ x 25 = ♦ x 100
Session 3
- In this session the properties of multiplication are extended to division, using the same array presentation as previously.
- Use PowerPoint 2 to navigate the instruction. The two multiplication equations come from ‘seeing’ the equal sets as rows or columns in the array. For example, Slide One shows 3 x 8 as “three rows of eight” and 8 x 3 as “eight columns of three”. Slide Two shows the corresponding division equations, 24 ÷ 8 as “the number of rows of eight in 24” and 24 ÷ 3 as “the number of columns of three in 24”. Note that division is interpreted as measurement, that is, “How many sets of x go into z?”
- Provide your students with Copymaster 1 and Copymaster 3. Ask them to identify a multiplication basic fact on Copymaster 3, mark or cut out the matching array on Copymaster 1, then record the two multiplication and two division equations in their workbook. Then, have them explain to a partner where the four equations can be ‘seen’ in the array. Ensure students have opportunities to experience both tuakana and teina roles with this task.
- Are there examples where there is only one multiplication equation and one division equation? With square arrays, such as 6 x 6 , there is only one division equation, 36 ÷ 6, since both factors are the same.
- Pose the following division word problems and have the students work together to solve them. The context for these problems should be adapted to reflect the context of your class. Copymaster 3 can be used by students as reference point
- A local business has donated 36 apple trees to be planted in the community garden at the marae. Gina wants them to be in rows of 4 trees. How many rows of apple trees could she make? Can you draw a diagram of this?
- Another business has donated 32 pear trees to be planted in the same garden. Hoani wants to plant these trees in 8 rows. How many should be in each row? Can you draw a diagram of this?
Give the students the following division problems and have them collaborate (mahi tahi) with a partner to solve them. Allow them to use Copymaster 3 to support them if necessary.
18 ÷ 3 = ?
36 ÷ ? = 9
? ÷ 5 = 8
28 ÷ ? = 4
48 ÷ 6 = ?
28 ÷ ? = 4
35 ÷ ? = 7
? ÷ 3 = 21
Discuss which facts you look for to solve ? ÷ 3 = 21.
Do your students look in the three times tables to look for a product of 21?
Construct arrays where necessary.
- Slide Six of PowerPoint 2 has a multiplication grid with many of the factors missing. Challenge your students to copy the grid into their workbook and complete it so that all the facts work. Animations on the slide can be used to get them started and provide the solution once students have worked on it.
- Discuss the best way to approach the solving of the grid.
- Extension: High achievers might enjoy creating grids for other students to solve.
Session 4
In this final session students work on the relationship between the distributive property of multiplication and strategies for solving division problems.
- Begin with the division problem: 42 ÷ 3 = ?
What multiplication equation could we write to solve this problem? (? x 3 = 42)
Both equations are asking us, “How many threes are in 42?”
- Use Slide One of PowerPoint 3 to work through a solution.
Where is the answer to both equations?
Do your students recognise that 10 + 4 = 14 is the number of fours found in 42?
- Continue with Slides Two and Three of PowerPoint Three to provide other examples of the distributive property applied to division.
- Give students the following problems to solve in pairs or threes. Provide Copymaster 1 so your students can model the problems with arrays if they need to.
39 ÷ 3 = ?
108 ÷ 9 = ?
56 ÷ 4 = ?
75 ÷ 5 = ?
84 ÷ 6 = ?
91 ÷ 7 = ?
Encourage students to record their strategies using multiplication or division equations.
- Share solutions and have a korero about strategies as a class
- Provide students with Copymaster 4 to work from. The work involves dividing 72 into various measures. Look for students to:
- Leverage off previous answers, e.g. If 72 ÷ 4 = 18 then what is 72 ÷ 8? There are half as many eights, as there are fours, in 72.
- Apply the distributive property of multiplication to division, e.g. 10 x 4 = 40, and 8 x 4 = 32, so 18 x 4 = 72.
- Creatively combine strategies where a fact is unknown, e.g. 2 x 16 = 32 so 8 x 4 = 32, using doubling and halving with the commutative property.
- High achieving students can look at all the possible equal teams that can be created with numbers like 72, 96, 100, 120 or 144 pūkeko. This can lead to methods of finding all the factors, and divisibility rules (see Pages 72-74 of Teaching Multiplication and Division)