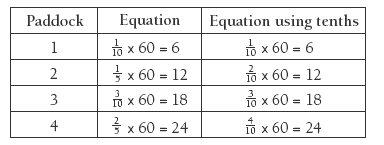This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (498 KB)
use multiplication facts to solve problems
know equivalent fractions fro tenths and fifths
find half of a number
Number Framework Links
Students using advanced counting (stage 4) strategies can solve these problems using materials.
Use this activity to:
• help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in all three operational domains (addition and subtraction, multiplication and division, and proportions and ratios)
• encourage transition from early additive strategies (stage 5) to advanced additive strategies (stage 6)
• help your students to consolidate their knowledge of co-ordinating numerators and denominators in fractions and simple equivalences (fractional numbers, stages 6 and 7).
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book One, Emu Auctions, page 20
This activity encourages students to use diagrams of farm regions to help them find fractions of sets of emus. There is a wide range of strategy options available to students who have access to materials and diagrams.
Introduce this activity through guided teaching rather than as an independent activity unless your students are confident at stage 6 or above on the Number Framework and have a good understanding of equivalent fractions.
The students can clarify the problem by making a diagram of the farm in question 1. Share a number of alternative arrangements for the farm paddocks, for example, paddocks arranged as grids in patterns of 4 x 4 or 8 x 2.
Ask the students using imaging:
How many paddocks of 6 emus do you think can be filled with 54 emus?
Now image the rest of the paddocks to work out the total needed to fill the farm.
Those students who find this too difficult could use materials to model all the emus on their diagrams and find out how many will fill the farm if 6 go in each paddock. If they use counting strategies, ask them to try and find the total again without counting. This will encourage part–whole thinking.
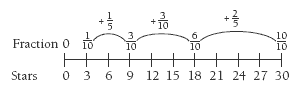
The question 2 scenario may need clarification. Relate the fractional size of the paddocks to the farmer’s plan for equal space for each emu. In the Numeracy Project Material Master 7-8, Mystery Stars, there is a circle divided
into tenths with 3 stars in each tenth. Use this to explain the equivalent relationship between fifths and tenths and how if 1/10 holds 3 stars, then holds 6 stars. You could also use it to show how 1/10 + 1/5 + 3/10 + 2/5 = 1.
On a double number line, compare the 30 stars on the whole circle of the material master with the fractions used in the problem:
Now ask the students to image 60 stars on the whole circle and find out how many are in each fraction. Connect this problem to the problem in question 2. If necessary, the students could draw another number line using 60 emus instead of 30 stars.
Have the students use number properties to find the number of emus in each paddock. They could record their working as equations in a chart like the one below. A third column could show the equations using tenths. For example:
In question 3, explore the fraction that Maafi’s father buys from each lot. Material Master 7-7, Fraction Strips, or a fraction board will be an ideal tool for this. The students will need to use 4 strips that join up to make 1 whole. These strips need to match the conditions in the question. They should find 1/2, 1/4, and 2 lots of 1/8 strips. Compare these to the box diagram so that the students connect these models to the problem.
Encourage the students who use imaging to image the number of emus on each part of the box diagram. If necessary, the students could use materials and model each emu. Discuss ways to work out the problem using numbers and have the students attempt to write equations, for example:
1/2 x 64 = 32
1/2 x 32 = 16
16 ÷ 2 = 8
Answers to Activity
1. a. 42 emus. (16 x 6 = 96. 96 – 54 = 42)
b. 7 paddocks. (54 ÷ 6 = 9. 16 – 9 = 7)
2. Paddock 1: 6 emus (1/10 x 60 = 6); paddock 2: 12 emus; paddock 3: 18 emus;
paddock 4: 24 emus
3. Lot 1: 32 emus (1/2 x 64 = 32); lot 2: 16 emus; lot 3: 8 emus; lot 4: 8 emus