Purpose
The purpose of this activity is to support students anticipating the result of dividing a whole number by 100.
Achievement Objectives
NA3-1: Use a range of additive and simple multiplicative strategies with whole numbers, fractions, decimals, and percentages.
NA3-2: Know basic multiplication and division facts.
NA3-4: Know how many tenths, tens, hundreds, and thousands are in whole numbers.
Required Resource Materials
- Place value people (make thousands from ten 100-squares stapled together)
- Place value board (page 1)
- Calculator
Activity
- Pose problems that require students to divide a two-digit whole number by ten. For example:
Make the number 500 with place value blocks.
What number have I made?
If I make each block 100 times smaller than the size it is now, what number would I have? (5) How would we describe the size of the new number? (one hundredth of the previous number)
Let students predict the result. You may need to address student knowledge of one hundredth as the result of equally partitioning an amount into 100 equal parts.
- Model dividing units by 100 by exchanging each flat block (a hundred) for a long block (a ten) and each long block (a ten) for a unit cube (a one). Move the blocks into their relevant place value columns.
What number have we made? What is different about 500 and this number? Emphasise that the new number, 5, is one hundredth of the original number, 500, because it is one hundred times smaller and 100 lots of 5 fit into 500.
Can we write an equation to describe this problem? (E.g. 500 ÷ 100 = 5).
Key in 500 ÷ 100 = 5 on the calculator and record the equation.
- Let the students anticipate, and then solve, similar problems with materials. Model the operation with place value blocks, if necessary, until students anticipate the result. Good examples are shown below. Ensure students express the relevant equations, using a suitable means of expression (e.g. written, verbal), as they work. Also consider allowing students to work in groupings that will encourage peer scaffolding and extension. Some students might benefit from working independently, whilst others might need further support from the teacher.
What number is one hundredth of 300?
What number is one hundredth of 800?
- Repeat this process with numbers like 1400. Use blocks of ten hundred squares stapled together to represent thousands.
- Make 1400 using place value materials.
- Discuss what happens to 1400 and the place value materials when the number is divided by 100. Illustrate that 1000 partitioned in 100 equal parts creates ten (a strip of ten people). Exchange each square of 1000 for a ten strip, and each 100 for a single people.
What number is one hundredth of 1400? (14)
What equation can we write for this problem?
Key in 1400 ÷ 100 = 14 on the calculator and record the equation. You could write 1/100 x 1400 = 14 or 0.01 x 1400 to reinforce the connection to fractions and decimals, if appropriate.
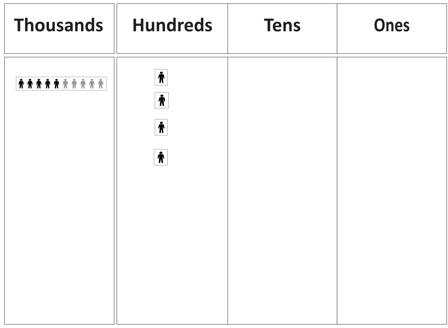

- Let the students anticipate, and then solve, further problems that involve dividing a four-digit number by 100. Model the operation with place value blocks, if necessary, until students anticipate the result. Use the calculator operation to encourage trust in the result. Good examples are shown below. Ensure students express the relevant equations, using a suitable means of expression (e.g. written, verbal), as they work. Also consider allowing students to work in groupings that will encourage peer scaffolding and extension. Some students might benefit from working independently, whilst others might need further support from the teacher.
What number is one hundredth of 2600?
What number is one hundredth of 3700?
Next steps
- Progress from using materials to anticipating the results using only equations and words, and then patterns. Calculators can be used to confirm predictions. For example:
- 6000 ÷ 100 = 60
- 6700 ÷ 100 = 67
- 6780 ÷ 100 = 67.8 (What does the eight refer to? How are tenths created?)
- 6789 ÷ 100 = 67.89 (What does the nine refer to? How are hundredths created?)
- Discuss what happens to the place values of different numbers as they are divided by 100 (they are made one one-hundredth of the size).
- Each one becomes worth one hundredth.
- Each ten becomes worth one tenth.
- Each 100 becomes worth one.
- Each 1000 becomes worth ten.
- Provide problems framed in real-life, meaningful contexts in which whole numbers are divided by 100. Examples might be:
- 100 calves drink 2670 litres of milk in a week. How litres do one calf drink in a week?
- How many $100 notes make $7,800?
- You need 9500 eggs to make a super omelet. The eggs come in trays of 100. How many trays do you need?
Add to plan
Level Three