Dicey Differences

In this activity, the students explore the concept of fairness by playing a game that turns out to be absolutely unfair.
The concept is extremely simple, and students are likely to get most out of the activity if they are allowed to play the game and investigate its fairness with minimal teacher guidance.
It should take no more than 10 rounds, as suggested in question 2, to establish that the game strongly favours one player. If students combine their results with those of others, as suggested in question 3, they will have enough data to provide some clear patterns.
These patterns could be confirmed by entering the totals into a computer spreadsheet and graphing the results as a bar graph. The resulting graph is likely to have a shape similar to this one:

Question 4 asks the students to try and explain the pattern of results. This requires them to move from the experimental (playing the game and recording outcomes) to the theoretical (looking for a mathematical reason).
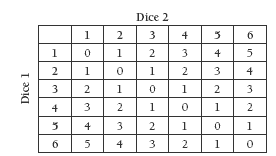
As a fi rst step, they need to consider all the possible outcomes when they toss two dice. The key to this is the understanding that the two dice must be treated as different and that the throw (2, 3 [a 2 on the fi rst dice and a 3 on the second]) is not the same as (3, 2). Equipped with this understanding, they can create a difference table (also found in the Answers). The numbers in the left-hand column represent the fi rst dice and the numbers across the top the second dice (not that it matters which dice goes where). The numbers in the body of the table are the resulting differences.

From this table, it can be seen, for example, that there are only two throws that will give a difference of 5 [(6, 1) and (1, 6)] but 10 that will give a difference of 1. This means that the probability of getting a difference of 1 is 5 times greater than the probability of getting a difference of 5.
There are 36 possible outcomes when two dice are thrown, so the probability of scoring a difference of 5 is 2/36 = 1/18 . It is important that students realise that this does not mean that if they throw a pair of dice 18 times, a difference of 5 will come up exactly once. Probability can predict long-run patterns, but it can never guarantee a particular result.

Answers to Activity

1. In round 1, differences of 0, 1, or 2 occurred twice as often as differences of 3, 4, or 5 (in fact, 5 didn’t occur at all!). In round 2, the differences of 0, 1, or 2 occurred three times as often as the differences of 3, 4, or 5. Over the two rounds, Maaka had 17 points to Whina’s 7, so it is not surprising that Whina thinks the game is unfair.
2.–3. Practical activity. Results will vary, but they will almost certainly favour by a big margin the player who gets points for a difference of 0, 1, or 2.
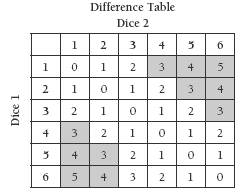
4. Comments will vary, but it should be clear that the lower differences turn up much more frequently than the higher differences, with 1 being the most common difference of all. If you create a difference table like the one below, it will be clear that the probability of a difference of 5 is 2 in 36 (1 in 18), while the probability of a difference of 1 is 10 in 36 (5 in 18). In other words, the probability of getting
a difference of 1 is 5 times greater than the probability of getting a difference of 5.

You could also shade the 3, 4, and 5 squares on your table and use these to discuss how much more likely it is to get a 0, 1, or 2 difference.

Key Competencies

Dicey Differences can be used to develop these key competencies:
• thinking
• participating and contributing