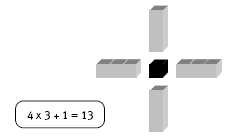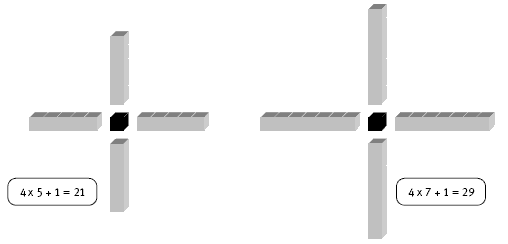This is a level 3 algebra strand link activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (268 KB)
use a table to find a rule for a geometric pattern
write rule to describe a relationship
FIO, Link, Algebra, Book One, Cube Signs, pages 4-5
multilink cubes
This activity further develops students’ abilities to predict patterns through the use of rules or equations. It also introduces them to the idea that the same pattern can be represented by different (but equivalent) equations.
In questions 1–4, the students develop and explain different short cuts or strategies for working out the number of multilink cubes in particular plus signs. The short cuts arise from different ways of visualising the structure of the plus signs. The students use the short cuts to predict the number of cubes in plus signs of any size.
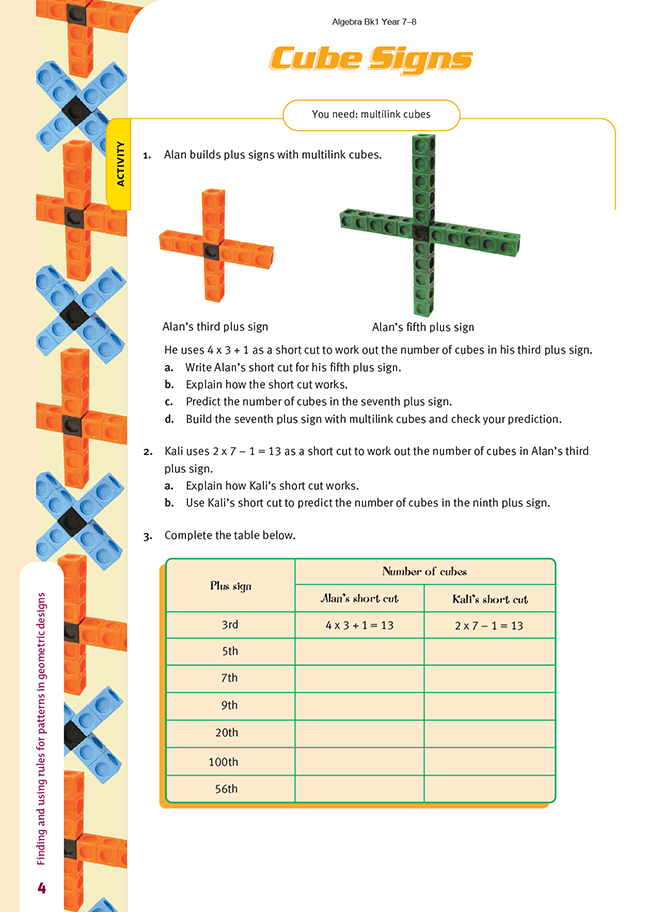
The students need to actually build the plus signs and then see if they can figure out how the physical models can be represented by the short cuts. For example, Alan’s third plus sign has 4 arms, each with 3 cubes, with 1 cube in the centre. So the short cut is 4 x 3 + 1.
The fifth plus sign has 4 arms, each with 5 cubes, and 1 cube in the centre, so the short cut is 4 x 5 + 1. The seventh plus sign has 4 arms, each with 7 cubes, and 1 cube in the centre, so the short cut is 4 x 7 + 1.
In question 2, the students should build the third plus sign with multilink cubes to match the short cut 2 x 7 – 1 = 13. As noted in the Answers, they need to take into account that the centre cube is initially counted twice.
Students who have difficulty seeing that 2 x 19 – 1 is Kali’s short cut for the ninth plus sign, where the 19 is found from 2 x 9 + 1, may need to build models with multilink cubes. They should explain how, for example, the short cut for the fourth plus sign is 2 x 9 – 1; how the short cut for the fifth plus sign is 2 x 11 – 1; and
so on. The table in question 3 provides an opportunity for the students to use the short cuts they have modelled with multilink cubes. They should also see that the different short cuts generate distinct rules that have exactly the same outcomes for particular plus signs of any size. Each rule is dependent on the way we see the cubes that make up the plus signs. As we change our point of view, we find new opportunities to express generality.
As noted in the introduction to these notes, students at this stage are not expected to use algebraic language, but there may well be students in your group or class who are ready to do so. The notes on algebraic language given here and for later pages are to help you to assist these students.
In algebraic language, the rules are 4 x x + 1 (Alan’s) and 2 x (2 x x + 1) – 1 (Kali’s), where the symbol x stands for the number of cubes in each arm of any plus sign. These rules are usually written more simply as
4x + 1 and 2(2x + 1) – 1. The multiplication sign is left out so that, for example, 4 x x becomes 4x (four times x is the same as four x). 2(2x + 1) – 1 and 4x + 1 give the same result for any value of x, so it is sensible to assume that 2(2x + 1) – 1 can be reduced to 4x + 1. The algebraic manipulation involved in this is
2(2x + 1) – 1 = (2 x 2x) + (2 x 1) – 1
= 4x + 2 – 1
= 4x + 1.
In question 4, encourage the students to look for more than one short cut. Two short cuts for the fourth plus sign are shown below.
Again, the best way for the students to identify short cuts is for them to make plus signs with multilink cubes. They need time to experiment and test the short cuts and to see if they can use them to develop a rule that in turn can be used to work out the number of cubes needed for the 75th or 123rd plus sign, and so on. Using more than one rule checks the accuracy of both the rule and the arithmetic in the calculations.
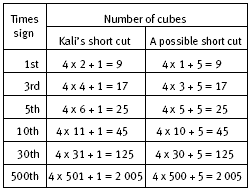
In question 5, the plus sign has been tilted and the arms extended. This means that the numbering of the plus and times signs are different. For example, Kali’s first times sign has the same number of cubes as Alan’s second plus sign. Likewise, in the fifth times sign, each arm has 6 cubes, with an additional cube for the centre of the times sign. So the fifth times sign has 4 x 6 + 1 = 25 cubes.
Another way to build the fifth times sign is:
Here, each arm has 5 yellow cubes. There are also 5 black cubes, one for the centre and one on the end of each arm. So the short cut is 4 x 5 + 5 = 25.
The table in question 5 provides an opportunity to consolidate the students’ use of the different rules that arise out of the different ways of seeing short cuts. The number of cubes for the 500th times sign can be very quickly calculated as 2 005 using either rule, and this demonstrates the power of generalisations and algebraic thinking. The algebraic rule for the xth times sign arising from the short cut 4 x 6 + 1 for the fifth times sign is 4 x (x + 1) + 1. This is the same as 4(x + 1) + 1, which simplifies to 4x + 4 + 1 = 4x + 5. The algebraic rule arising from 4 x 5 + 5 for the fifth times sign is 4 x x + 5, which is the same as 4x + 5. So the two rules are in fact equivalent.
Answers to activity
1. a. 4 x 5 + 1
b. Each plus sign has 4 arms, and there is 1 cube in the centre. In the third plus sign, there are 3 cubes in each arm. So, altogether, this sign has 4 x 3 + 1 cubes. The fifth plus sign has 5 cubes in each arm. So, altogether, the sign has 4 x 5 + 1 cubes.
c. 4 x 7 + 1 = 29
d. The seventh plus sign has 4 arms, each with 7 cubes, and there is 1 cube in the centre of the plus sign. Altogether, there are 29 cubes in this sign.
2. a. Kali sees the plus sign as a horizontal strip of 7 cubes and a vertical strip of 7 cubes, which is 2 sets of 7 cubes. But the centre cube has then been counted twice, and so 1 cube must be removed or subtracted. So the short cut is 2 x 7 – 1.
b. 2 x 19 – 1 = 37
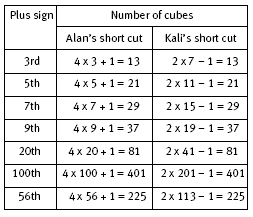
3.
.
4. a. One short cut is 4 x 4 + 2 = 18, and another is 2 x 9 = 18. Other short cuts are possible. In the first short cut, 4 x 4 + 2 = 18, there are 4 arms with 4 cubes, plus 1 extra cube at the bottom and another at the centre. In the second short cut, 2 x 9 = 18, there are 9 cubes in the horizontal arm and 10 – 1 cubes in the vertical arm (because the centre cube has been counted in the horizontal arm).
b. 4 x 75 + 2 = 302 cubes using the first short cut or 2 x 151 = 302 cubes using the second short cut 5. a.–b. The fifth times sign has 4 arms, each with 6 cubes. There is 1 cube in the centre of the times sign, so the short cut 4 x 6 + 1 = 25 does
work.
c. Answers may vary. One possible short cut is 4 x 5 + 5 = 25. A model that matches this short cut might have 4 arms, each with 5 identical cubes, and then a further 5 cubes, 1 for the centre and 1 on the end of each arm. Another possible short cut is 4 x 7 – 3. This is 4 arms of 7, minus 3 for the 3 arms in which the
centre cube is subtracted.
d.