The purpose of this activity is to support students in extending their understanding of multiplication of a whole number by a non-unit fraction. Problems include increases in the difficulty of both the fraction operator and the amount being operated on.
- Counters, tiles, or cubes
- Paper and pens.
- Imagine you have 24 counters. I will give you a different fraction each time. Find that fraction of 24.
- Find three quarters of 24 counters (3/4 x 24 = 18)
- Find five eighths of 24 counters (2/3 x 24 = 16)
- Find five sixths of 24 counters (5/6 x 24 = 20)
- Find seven twelfths of 24 counters (7/12 x 24 = 14).
- Together, reflect on the process of finding a non-unit fraction of 24.
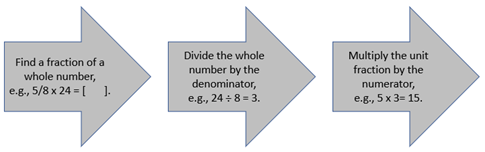
What did we do first? (Found the unit fraction of 24)
What did we do next? (Multiply the unit fraction by the numerator)
If necessary, use a physical model of one example to illustrate the process. Such as, find five eighths of 24 counters.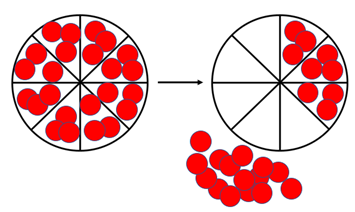
- Formalise the algorithm for finding a non-unit fraction of a whole number. Support the algorithm with an example.
- Pose similar halving problems about finding non-unit fractions of different numbers of counters, increasing the difficulty in terms of the basic facts required. The aim is for students to:
- Control the two steps: dividing the set by the denominator and multiplying by the numerator.
- Apply more difficult multiplication and division facts.
- Independently record the equations and demonstrate understanding of the meaning of the symbols.
Good examples are shown below. Consider what groupings will be most appropriate for your students. Whilst some may benefit from tuakana-teina relationships in structured peer groups, others are likely to be ready to work independently. Some students may also benefit from further teacher support. Consider also the different means of action and expression (e.g. verbal, written, digital, physical) that your students might use to demonstrate their thinking.
- Start with a set of 40
Get three quarters of the set (3/4 x 40 = 30)
Get three fifths of the set (3/5 x 40 = 24)
Get seven tenths of the set (7/10 x 40 = 28)
Get five eighths of the set (5/8 x 40 = 25). - Start with a set of 36
Get three quarters of the set (3/4 x 36 = 27)
Get four ninths of the set (4/9 x 36 = 16)
Get five sixths of the set (5/6 x 36 = 30)
Get two thirds of the set (2/3 x 36 = 24). - Start with a set of 56
Get three eighths of the set (3/8 x 56 = 21)
Get four sevenths of the set (4/7 x 56 = 32)
Get four quarters of the set (4/4 x 56 = 56).
Next steps
- Support students to increasingly difficult multiplication and division basic facts knowledge to anticipate the result of further problems. Good numbers of counters to use have many factors, such as 54, 64, 60, and 72. Encourage students to use one result to find another. For example:
- If three quarters of 56 equals 42 (3/4 x 56 = 42) what is three eighths of 56?
- If four fifths of 60 equals 48 (4/5 x 60 = 48) what is eight tenths of 60?
- If three ninths of 72 equals 24 (3/9 x 72 = 24) what is one third of 72?
- If seven eighths of 64 equals 56 (7/8 x 64 = 56) what is seven quarters of 64? (112).
- Explore equivalence with operators, such as If 6/8 of 72 equals 54, what are 3/4 and 9/12 of 72?
- Emphasise the idea of fractions that are equivalent to one by posing problems such as “what is seven sevenths of 49?” (7/7 x 49 = 49).