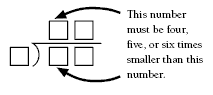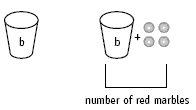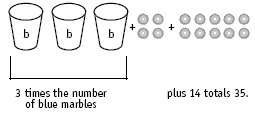These are level 3 measurement, algebra, and number problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (220 KB)
find volume of a cuboid (Problem 1)
continue a sequential pattern (Problem 2)
solve division problems (Problem 3)
use algebraic thinking to solve problems (Problem 4)
Problem One
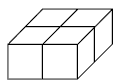
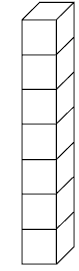
This problem involves students finding the volumes of three cuboids (rectangular prisms). Some students may need to use multilink cubes to build the cuboids. This is a very slow process, and discussion should focus on more efficient ways to find the number of cubes in each shape.
Many students are likely to apply an equal additions strategy. This involves finding the number of cubes in one layer or one column and repeatedly adding however many of these layers or columns are in the whole solid.
For example, cuboid b might be seen as:
four cubes in each layer 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28 cubes or
7 cubes in each column, 7 + 7 + 7 + 7 = 28 cubes.
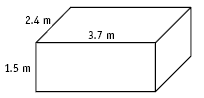
This equal addition of layers or columns is a step on the way to finding volume by multiplication, for example, finding the volume of cuboid b by saying 7 x 4 or 4 x 7. Finding volume by multiplication becomes much more important when the edges of the cuboid are not whole numbers. For example:
Volume = 1.5 x 3.7 x 2.4 = 13.32m3
So, in Problem One, the volumes are:
a. 3 x 3 x 4 = 36 cubes
b. 7 x 2 x 2 = 28 cubes
c. 2 x 5 x 3 = 30 cubes
Problem Two
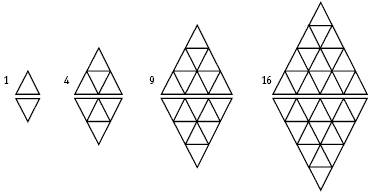
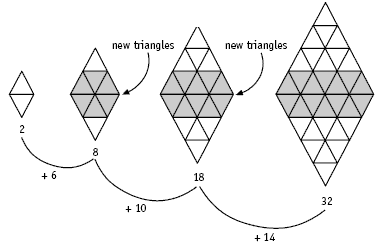
The number of triangles is increasing rapidly between one diamond and the next, so students will need to use patterns to make this problem easier to solve. Here are a number of po ssible approaches:
• Consider the diamond to be made up of two halves:
Students might recognise that the half numbers are square numbers, that is, 1 = 1 x 1,
4 = 2 x 2, 9 = 3 x 3, 16 = 4 x 4. So, the next half will be 5 x 5 = 25, and the whole shape should have 25 + 25 = 50 triangles.
• Consider the number of new triangles added each time:
There are four more new triangles each time, 6 + 4 = 10, 10 + 4 =14, so for the next diamond, there will be 18 new triangles. 32 + 18 = 50, so the next diamond will have 50 triangles.
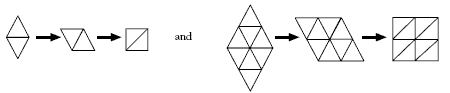
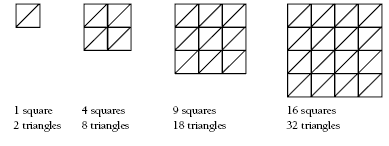
• The diamonds can be looked at as squares:
For example:
Each small square is made up of two triangles. So the pattern becomes:
The next diamond can be transformed into this square:
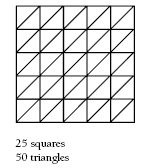
Problem Three
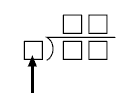
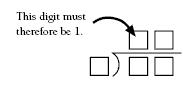
Students should use their knowledge of division to limit the location of digits in the set.
This digit cannot be 0 or 1. Division by 0 is undefined. Division by 1 would
mean that the digits in the answer would be the same as those in the dividend.
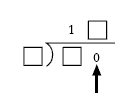
This number must be 0 because 10 cannot be the answer. (Only one 0 is available, and, in order to have an answer of 10, either the divisor or the dividend would need 0 as one of its digits).
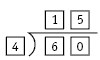
With this knowledge, students can try the combinations of locations for 4, 5, and 6 to find one that works:
This works!
Students may enjoy making up their own problems of this type. This is easier than solving them. Have them start with a known addition, subtraction, multiplication, or division result in which each digit is unique. For example:
Arrange the digits 2, 3, 4, 5, 6, and 8, one in each box, to make a correct multiplication.
Problem Four
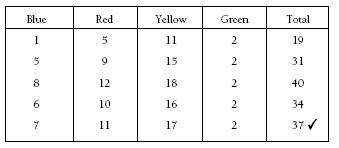
Students may solve this problem by trying various values for the number of blue marbles to see whether they work. For example:
An approach that involves algebraic reasoning might be:
• Two of the 37 marbles are green, so the other 35 must be blue, red, or yellow.
• Let an empty cup represent the number of blue marbles we don’t know:
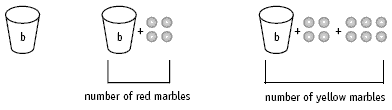
• There are four more red marbles than blue, so these amounts can be represented as:
• There are six more yellow marbles than red marbles, so all 35 marbles can be represented as:
• Collected, this means:
• Three times the number of blue marbles must equal 35 – 14 = 21.
21 ÷ 3 = 7, so seven is the number of blue marbles.
• 7 + 4 = 11 gives the number of red marbles.
11 + 6 = 17 gives the number of yellow marbles.
We already know that there are two green marbles.
Answers to Problems
1. Shape a
2. 50
3.
4. 11 red, 7 blue, 17 yellow, and 2 green