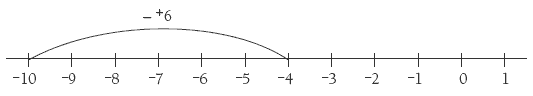Chilly Heights

Like the activity on the previous page, this activity involves positive and negative numbers. The addition and subtraction of integers is very meaningful for students at the advanced additive stage or beyond of the Number Framework.
Temperature variations in relation to height and wind chill are certainly factors that need to be taken seriously when out tramping or engaging in other outdoor pursuits. Search and Rescue services regularly report finding people suffering from hypothermia in the outdoors, often as a result of being ill-equipped for the conditions. The activities in Chilly Heights are therefore very relevant.
Like the years BC in the previous activity, temperatures below 0°C are effectively negative numbers. However, some of the questions in Chilly Heights require two or more calculations involving negative numbers.
In question 1, the students will have to calculate not only Jonathan and Penny’s increase in altitude from Plateau Hut to the top of the Linda Glacier (3 100 – 2 200 = 900 metres) but also the drop in the temperature felt, assuming that the temperature decreases 1°C for every 150 metres in altitude. The first step is to determine how many lots of 150 metres there are in 900 metres. Encourage the students to look for a strategy to work this out. For example, 150 x 2 = 300, and there are 3 lots
of 300 in 900 (because 3 x 3 = 9), so there must be 3 x 2 = 6 lots of 150 in 900. Therefore, 6° must be subtracted from –4°C to allow for the further drop in temperature (–4° – +6° = –10°). If the students are still unsure how to subtract a positive number from a negative number, you could show them this on a number line:

Question 2 is more straightforward. The sheltered temperature of –7°C is already given. All the students need to do is to read off the temperature on the wind chill temperature chart. Questions 3 and 6 can be approached in the same way.
Question 5 is not too dissimilar. The wind chill temperature with the 80 kilometres per hour wind, given a temperature of 4°C in the sheltered spot, is –4°C, a difference of 8°C. Again, a number line is a useful tool.
To calculate the temperature at Mt Cook Village (question 4), the students will find it necessary to:
i. work out the difference in altitude between the village (700 metres) and the summit of Aoraki (3 754 metres);
ii. work out how many lots of 150 are in their answer to i (to find how many lots of 1°C the temperature is increasing with the drop in altitude);
iii. add this increase in temperature to the –4°C registered on the thermometer at the summit.
To answer each part, the students can use the strategies suggested for earlier questions in this activity.
Possible extensions of Chilly Heights would be for the students to investigate:
• the temperature at the heights that different aeroplanes and gliders typically fly
• the difference in temperatures on the wind chill temperature chart from 7°C through to –10°C . For example, at the 7°C mark, the perceived temperature drops by 7°C as the wind increases from 0 to 80 kilometres per hour, whereas at the –10°C, the temperature drops twice this amount to register –24°C.

A handy website relating to height, altitude, and temperature is: http://earthsci.terc.edu/content/investigations/es1702/es1702page05.cfm
This website includes a graph of decreasing temperature with increasing altitude based on data collected from a balloon ascent in Wyoming on 20 August 2001. The graph shows a steady decrease in temperature from about 2 000 metres up to an altitude of about 12 500 metres. It also mentions that commercial jet aeroplanes typically fly at an altitude of about 12 000 metres, at which height the graph shows a temperature of approximately –60°C. Within New Zealand, jet aircraft reach
an altitude of about 9 000 metres, while turbo-prop aircraft typically fly at about 5 000 metres unless they are only flying short distances, in which case they tend to reach a height of about 2 000 to 2 500 metres.
 

Answers to Activity

Activity
1. –10°C
2. –14°C
3. –13°C
4. About 16°C. (The difference in height is 3 754 – 700 = 3 054 m. 3 054 ÷ 150 = 20.36. 20.36° + –4° = 16.36°)
5. 8°C. (4° – –4° = 8)
6. 4°C