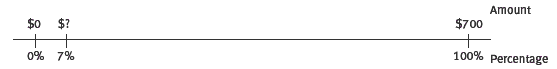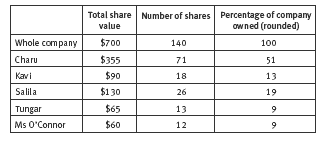This is a level 4 number and algebra activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (3031 KB)
find a percentage of a decimal number
solve addition and subtraction problems
compare prices by using proportions
Number Framework Links
Students need to be strong multiplicative thinkers to solve the problems in these activities. They need to be working at stage 7 at least, although some of the questions involve proportional reasoning at stage 8.
For example, calculating interest payments involves using a percentage (decimal fraction) as an operator and finding what fraction of the company each person owns involves the part–whole construct of fractions.
classmate
calculator
spreadsheet program (optional)
Activity One
Financial language
Business, income, profit, loan. (See the full glossary at the end of these teachers’ notes.)
Financial understanding
In this scenario, Charu puts her cooking skills to work to earn a profit. She investigates setting up a chutney business, but first she budgets for what she will need to pay out in costs. Through her business, students will explore how businesses are set up and run. They will also examine where the mone could come from to start up
her business.
The scenario introduces a range of financial ideas and business terminology that your students need to understand if they are to work independently on the activities. You may choose to teach these ideas first and then use the pages as application of the ideas and processes. Alternatively, you could work through the activities with your students in co-operative groups, teaching ideas as they arise. This is arguably a better approach because the students can apply their real-life experiences in developing the ideas.
Let the students read the first page together without answering the questions. Leave defining unknown words until the scenario is discussed.
Ask: What is Charu trying to do in this story? She is trying to set up a business (an economic organisation that produces goods and services for a profit). In Charu’s case, the goods are jars of chutney.
Why would she do that? To earn income. The money you earn from working and from other sources, such as profits from a business or interest on money saved, is all part of a person’s income. Charu also has a real interest in cooking and in setting up a business; given both those aspects, she should follow her dreams and give it a go.
That is how she will learn about herself, her capabilities, and her skills.
Will all the money Charu earns from sales be income? That is, does it all get paid to her? No, she will have to pay other people money for things she buys from them to run her business. Money paid out to others will be for her usiness start-up costs and her ongoing operating expenses.
Why are Charu’s outgoings highest when she starts her business? She needs to buy equipment and ingredients to get the business going. Some of these expenses are “one-offs”, such as pots and cooking utensils, and some costs will occur each time she makes a batch of chutney, for example, the fruit for the ingredients.
Start-up capital is the money Charu needs to get the business going. Where might she get this capital? Charu may already have money herself in her savings that she is prepared to invest in her business. However, if she does think about using her own money, she needs to consider the opportunity cost – might she be better off
using someone else’s money and keeping her own separate? If she doesn’t have enough capital, she might borrow money from someone else or from a bank. Note: Loans are liabilities, not capital.
If she borrows money, how does that work? Charu will need to pay that money back. She will probably also need to pay interest, that is, as well as paying back the money she has borrowed, she will pay some extra money to the lender for the use of their money.
What might change the amount of interest Charu pays back? The amount of money she borrows, the interest rate charged, and the amount of time it takes to repay the loan:
• The more Charu borrows, the more interest she pays.
• Interest rates can vary. They can vary according to the length of time for which you want to borrow the money, for example, a 6 month loan may be more expensive than a 2 year loan. Also, different banks and other lenders can and do lend at different rates. It pays to shop around for the best deal. Interest rates are written as a percentage and give a time period over which the interest is charged. For example,
10% p.a. means ten percent (one-tenth) charged per annum (every year).
• The period of time she has the money for before she pays it back will affect the amount of interest she pays. If she has it for 3 years, she will usually pay interest throughout that time. In fact, if her repayments are very low, she might end up paying interest on the interest. This is called compound interest.
Why is it important for Charu to create a budget? So she can plan what her income and expenses might look like ahead of time. Financial planning is important for personal and business financial success. This avoids her trying something that won’t work and tests whether a business is viable and potentially profitable. A budget enables Charu to identify, manage, and assess risk.
For Charu to see this business venture through, she needs to apply initiative, drive, and planning. Without these, the chance of success is reduced. (Things still happen, but are they what the business person wants to happen?)
After these discussions, the class could work through questions 1 and 2 together (see the Mathematics and Statistics section on page 20). Some aspects of question 3 may need to be discussed before the students work independently in small groups on that question. See below and also, mainly for extension, the comments on spreadsheet construction in the Mathematics and Statistics section for this activity. The students should be able to work independently in small groups on question 4. Refer to the Answers for ideas on discussing which bank gives the best deal.
Question 5 involves a further comparison. Discuss the reasons why Charu may or may not take Grandad’s offer. Central to any financial discussion are the key financial messages for students. Charu knows that a good financial decision will bring benefits; she will be looking to choose the one that brings the most benefit to her business. She realises that interest payments are an expense, an additional cost that has to be taken
into account, and she discovers that an inverse relationship exists between the time taken to repay a loan and the amount repaid each week, month, and so on.
The students might use a spreadsheet, as shown in question 3, to explore Grandad’s scenario under different repayment options. Keeping the repayment amounts simple helps them to recognise the inverse relationship. You may need to point out that the “unpaid balance” amounts in the spreadsheet in question 3 (and in the ones shown below) is the balance at the end of each month after the repayment and interest portion (on the same row) are taken into account. The spreadsheet would be constructed differently if the “unpaid balance” was that shown at the beginning of the month, before repayments. (You could also discuss with them the possible complications of borrowing money from family members. For example, if Grandad’s
offer wasn’t as good as that from a loan company, Charu may have to decide, for financial reasons, to run the risk of Grandad being upset! There can be other complications with involving family members that people need to consider carefully, such as when a family member lends money in good faith but then needs it back sooner than expected or when the person lends the money and then expects to have a say in how the business is run.)
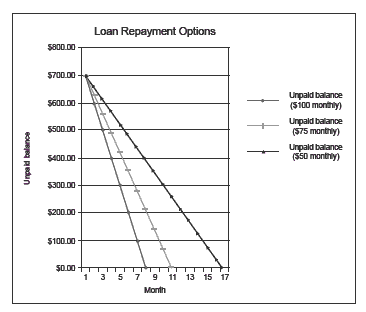
The spreadsheet below shows some different repayment options ($100, $75, or $50 per month).
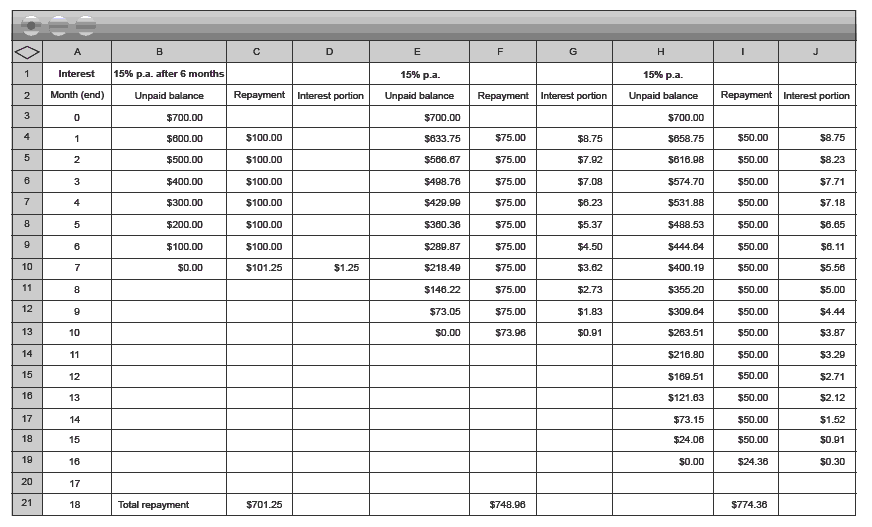
The students might find it interesting to graph the unpaid balances under the different repayment scenarios and compare them to the earlier loan company repayment scenarios.
The spreadsheet and graph shows that Grandad’s plan is good for Charu if she can manage high repayments in the early months of her business. This will mean she pays
little or no interest. However, if she can only manage small repayments, such as $50 or less a month, then she could end up paying more interest than she would through the loan companies.
The key idea is that Charu must decide whether the risk of taking Grandad’s loan, with a higher rate of interest after 6 months, is justified because she will pay no interest in the first 6 months and whether she can manage the risk through meeting high repayments over this time.
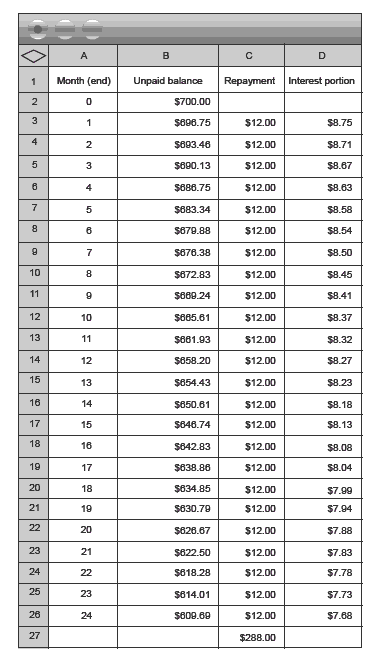
Another all too common scenario is where the monthly repayment is so low that very little money ends up being paid off the principal after quite a long period of time (and
in some cases, the interest ends up being more than the repayment amount, so the principal grows!). For example, if Charu borrowed $700 and repaid it at $12 a month at 12 percent per annum, at the end of 2 years she would have paid $288 and still owe $609.69, as shown in this spreadsheet:
You also could have a useful discussion about the advantages and disadvantages of an interest-only loan. For someone just setting up a business and with limited
income, the smaller payments could help them stay viable until they are established and have a better cashflow. However, there are disadvantages as well. For example, if Charu had an interest-only loan for the first 2 years at, say, 10 percent, at the end of that time she would have paid the loan company $700 x 10% x 2 = $140, but she would still owe just as much as when she started, that is, $700, which she would still be paying interest on while she is repaying the principal.
Mathematics and statistics
Allow the students to work through question 1 co-operatively and then share their answers. These can be checked independently against those given in the Answers section.
Question 2 involves the calculation of interest. Students will need to understand how to:
1. calculate a percentage of an amount
2. enter formulae into a spreadsheet so that the computer calculates the interest for them.
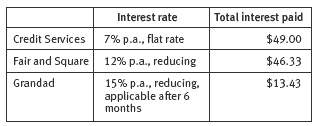
Begin with the Credit Services scenario in which a flat rate of 7 percent per annum (p.a.) interest is charged. Strip diagrams, ratio tables, and double number lines provide useful graphical aids to solve proportional reasoning problems, such as finding percentages.
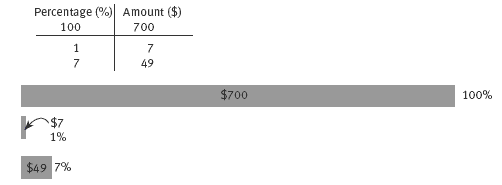
Consider the task of calculating 7 percent per annum interest on $700. A double number line representation would look like this:
In this case, students need to establish some benchmarks for calculation. For example, finding 10 percent and halving that to find 5 percent gives boundaries for estimating 7 percent (between $35 and $70).
$0
Alternatively, finding 1 percent, possibly by finding one-tenth of 10 percent, gives the required benchmark for calculating 7 percent. This is called a unit-rate strategy, that is, 1 percent is $7, so 7 percent is $49 (1:7 is the unit rate).
This unit-rate strategy is just like the standard algorithm, for example, 700 x 7/100 = = because 700 ÷ 100 x 7 = 7 x 7 = 49.
Ratio table and strip diagram representations of the same problem might look like this:
It’s important for students to realise that interest is charged in addition to the amount borrowed, so Charu has to pay back both the borrowed amount and the interest. So paying the loan back in a one year scenario for Credit Services looks like this:
Total to pay back equals $700 + $49 = $749
Dividing by 12 gives the monthly repayments.
Question 2c involves an additional step in that Charu will pay 2 x 7% = 14% interest on $700 if she chooses to repay it over 24 months.
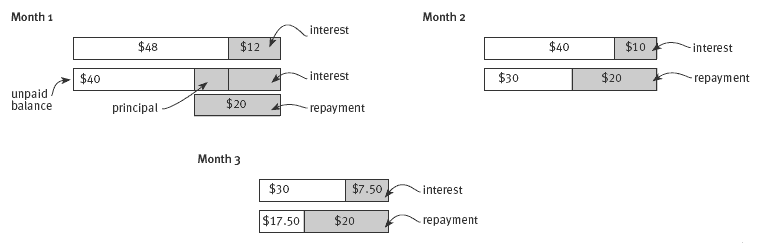
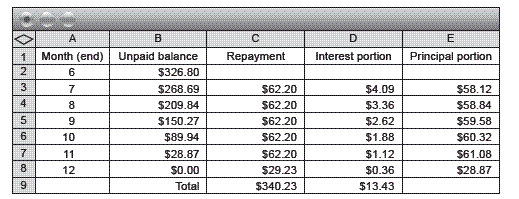
For question 3, the students need to understand tables of repayments and the concepts of interest and principal repayments. On any loan, part of a repayment is straight interest, paid to the bank for the privilege of using their money for a given time. Part of the repayment will be principal. The principal is the amount still
owing to the bank from the original money borrowed, so as the loan progresses, more of the borrowed money is paid off. This means that the interest accrues on a decreasing amount of principal as the loan progresses. The repayments are usually fixed, so the proportion of principal paid off increases as the months go by,
whereas the amount of interest decreases. One way to illustrate this is take a simpler scenario. Suppose that someone takes out a $48 loan at an interest rate of 25 percent per month. They pay off $20 per month.
Students do not need to understand how the spreadsheet in question 3 was developed, although this provides excellent opportunities for extension. It’s important for the students to realise that 12 percent per annum interest applies at a rate of 1 percent per month.
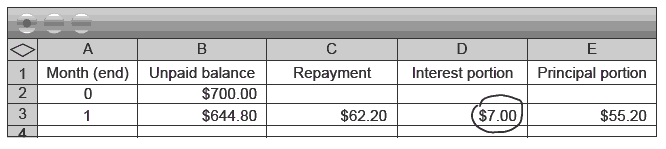
Ask Why is this figure $7.00?
Fair and Square Finance charges 12 percent per annum or 12 percent over 12 months. Therefore we can do the same calculation using 1 percent per month. The spreadsheet has calculated 1 percent of $700. (This was done using the function =B2*0.01)
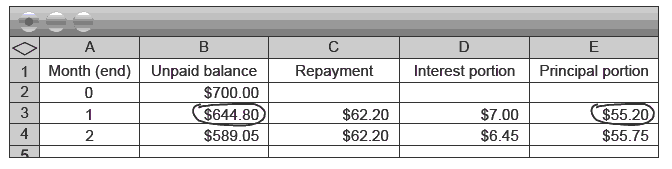
Ask Why are these figures $644.80 (instead of $700) and $55.20?
The spreadsheet has worked out (using the function =C3–D3) how much of the $62.20 repayment ($55.20) went towards paying off principal. This amount was then taken off the unpaid balance (using the function =B2–E3) to get $644.80. Find out if the students can see the cyclic nature of the spreadsheet by challenging them to work out how the amounts $6.45 and $55.75 were calculated and why the unpaid
balance in B4 is $589.05.
Social Sciences Links
Achievement objectives:
• Understand how people make decisions about access to and use of resources (Social Studies, level 3)
• Understand how exploration and innovation create opportunities and challenges for people, places, and environments (Social Studies, level 4)
The main resource in this activity that creates opportunities and challenge is money. Have the students discuss:
– how the different interest rates might affect Charu’s decisions about access to and use of resources
– how the cost of money has impacted on her budget. Could she make some different decisions? For example, does she need to spend $180 on a gas stove? Could she simply use the stove at home? Is this fair, and who and how could she pay for access to this resource?
There are other areas that can also be explored, such as the cost of accessing money.
Activity Two
Financial language
Shares, dividend, start-up capital
Financial understanding
In this activity, Charu explores other sources of money to start her business. She decides to raise money through a share issue. The capital she raises through these shares means that she has shareholders (co-owners of her business). If she makes a profit, she will pay them a dividend (a share of the profit based on the number of shares owned).
Charu collects, organises, and analyses information as she looks for the best way to finance her business. She will also be negotiating with and influencing those people interested in being shareholders in her business. Having good financial information to give them will be very important to her success.
Some students may have prior knowledge about shares; others may not. Ask:
Charu is going to issue shares in her company. What does that mean? In return for providing Charu with money to use as capital, some people or organisations will own part of her company. These people or companies are known as shareholders.
Why do people buy shares in companies? Shares can be bought and sold. Sometimes, like houses, their value goes up; sometimes their value goes down.
What causes the price of shares to go up and down on the share market? The value of shares is a sign of what buyers and sellers think they are worth. Usually, companies that make good profits and pay their shareholders a reasonable part of these profits have shares that increase in value. The part of the profits paid to shareholders for each share is called a dividend.
Before the students attempt questions 3 and 4, discuss the term “profit” with them. This is the amount of money a business has left over from their revenue after it has paid its expenses. Profits paid out as dividends are usually allocated to shareholders on a “per share” basis. Deciding how much each shareholder gets paid is another example of proportional reasoning. Also note that, although for some people profit is the motivation for setting up a business, equally important for others is the incentive to
take an idea or personal talents and see if they will sell in the marketplace.
Mathematics and statistics
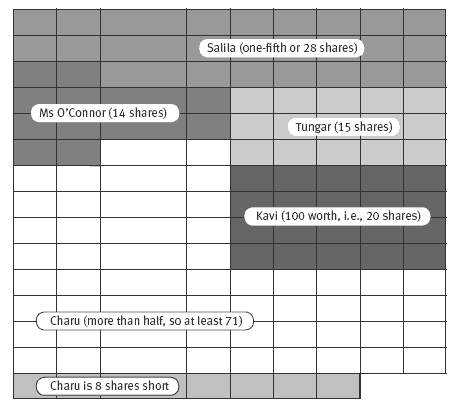
In this activity, Charu is creating $5 shares in her company. Her company needs $700 starting capital, so this means that there will be 140 shares (700 ÷ 5 = 140 or 5 x 140 = 700). If she owns more than half the shares, Charu will have a controlling interest in the company. She needs to own more than half the shares in case all the other shareholders combine to vote against her. Each share gives its holder one vote in making major decisions about how the company is run.
A diagram based on 140 squares (shares) may help the students work out how many shares can be given to each person. The first diagram (with 8 additional squares at the bottom) shows what they want.
This diagram shows that 8 more shares are needed than Charu has available. The next diagram shows how the 140 shares could be divided:
The students’ decisions about how to allocate the shares affect their answers to what percentage of the company each person owns. These percentages are best calculated using number of shares rather than the value of the shares. For example, Kavi’s $100 in shares equates to 20 shares at $5.00 each. Twenty out of 140 shares is one-seventh (1 ÷ 7 = 0.1429), so if Kavi is able to buy 20 shares, he would own 14.3
percent of the company.
To work out how much each shareholder gets paid in dividends, the students might use two different types of strategy and compare the amounts they come up with.
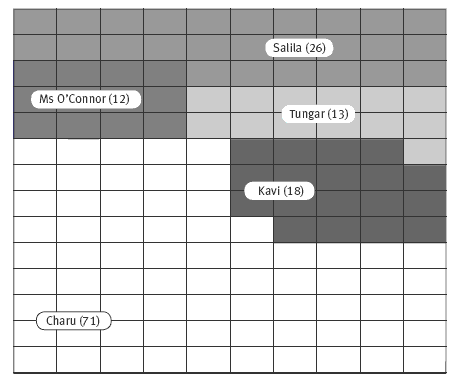
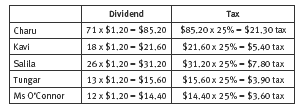
The first way is to find the unit rate per share. There are 140 shares and an expected profit of 6 x $28 = $168 in the year. So each share should be allocated 168 ÷ 140 = $1.20. The amount paid to each person is $1.20 multiplied by the number of shares they own. So if Charu owns 71 shares, she gets 71 x $1.20 = $85.20.
The other strategy is based on the fraction of the shares each person owns. If Charu owns 71 shares, she will receive 71/140 x $168.00 = $85.20. The first strategy uses a rate strategy (1 : 1.2 as 70 : 85.20), and the second strategy uses a fraction as an operator.
Discuss with the students what tax means. Most will know that their parents pay tax to the government on the money they earn. This means that a part of each dollar earned is taken by the government in tax to provide services like health, education, and superannuation. This part is known as the tax rate because it can be expressed as a comparison between money earned and money taken as tax. Tax is often expressed as “x cents in the dollar”, which can be expressed symbolically as x :1 (for example, $0.31 tax for each 1 [dollar] earned).
Calculating how much tax each shareholder will pay on their dividends is another problem that involves a fraction as an operator. The tax rate set for this activity is 25 percent. 25 percent is a fraction, 25/100, that can be more simply expressed as 1/4. So Charu, with 71 shares, will pay 1/4 x $85.20 = $21.30.
Reflective question
Financial understanding
If Charu doesn’t make a profit, it means that her business expenses are greater than the sales revenue from the business. To pay for the expenses, she will have to use her loan and, if that’s still not enough, her start-up capital (from shares sold). Making a loss is normal when a business first starts up, but if Charu’s cash flow is insufficient to continue running the business on an ongoing basis, then she would have to close down, knowing that some of her suppliers, her grandad, and her shareholders may not get their money back. Bankruptcy is a big risk in starting up a business. The shareholders are the last to be paid back.
Social Sciences Links
Achievement objective:
• Understand how the ways in which leadership of groups is acquired and exercised have consequences for communities and societies (Social Studies, level 4)
Have the students discuss how Charu is attempting to acquire leadership of her company (community) and what consequences this will have for:
– herself
– her shareholders
– the company.
Activity Three
Financial language
Costs, price, profits, sales revenue, operating costs (business expenses)
Financial understanding
For business success, Charu will want to make decisions that maximise her profit. Profit = sales revenue – cost of sales.
In this activity, through Charu’s business decisions, students explore the concept of “shopping around” and minimising business expenses. Charu has to set her prices for her chutneys; the prices set in her budgets must make a profit. She may also discover that if people really like her chutney, she can charge a higher price.
Charu’s actions of shopping around and setting prices to maximise profits are good business practice. This involves her in planning and organising, being flexible, and dealing with change, all of which are attributes that support good business practice.
Discuss with the students What might be the advantages and disadvantages of Charu “shopping around” to buy her fruit and vegetables at the best price from different stores?
The advantage is that potentially Charu might save money by getting the best deals from each market. The disadvantage is that she will use up time and transport going to three markets instead of one.
Another consequence is that Charu won’t establish a business relationship between herself and a single supplier. Such a relationship can help establish “goodwill”, which may mean the supplier provides extra goods and services free of charge or provides a discount for loyalty. A single supplier is more likely to provide continued supply of fruit and vegetables in times of scarcity than multiple suppliers.
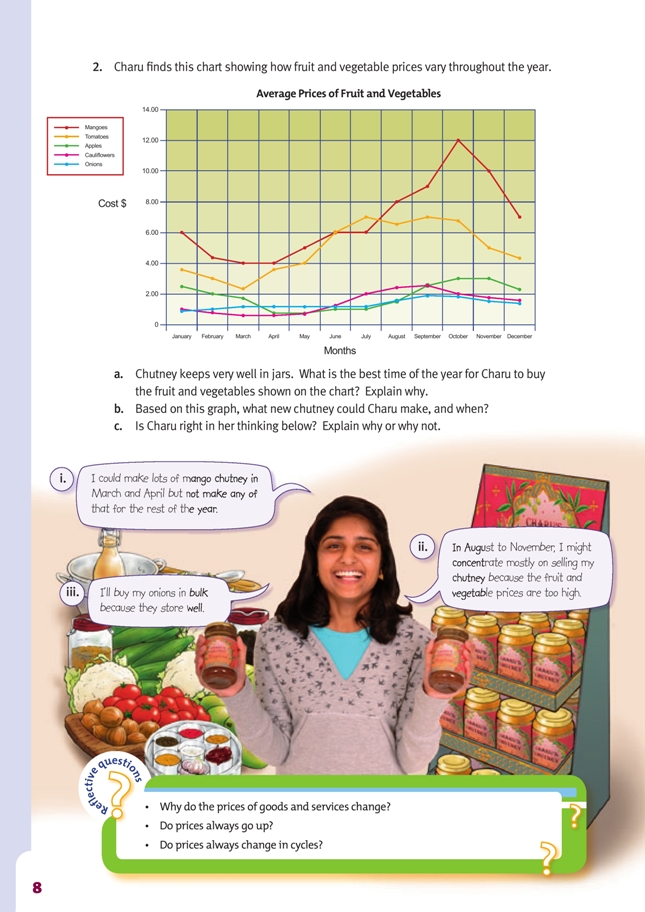
Get the students to work co-operatively through question 1 and to check their answers from the Answers section. Discuss the chart of fruit and vegetable prices. Ask Why are the prices cheaper in the first half of the year than they are in the second half of the year?
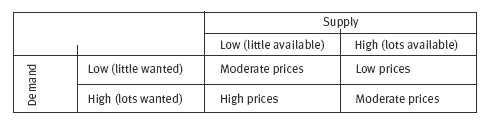
The prices of fruit and vegetables, like most goods and services, are determined by supply and demand. In the first half of the year, fruit and vegetables grow well and many fruits are picked during that time. This means that supply is high, with lots of fruit and vegetables for sale, usually at very reasonable prices. In the second half of the year, fewer fruit and vegetables are available for sale and prices tend to be higher.
Some of these products are imported from countries in the northern hemisphere, so the transport costs are higher.
The demand for fruit and vegetables varies little across the year. Some people store fruit and vegetables by freezing and bottling (canning) during the first half of the year when prices are lower, so the quantity demanded is slightly higher at these times. People won’t store fruit and vegetables unless it is cheaper to do so.
Question 2 is suitable for small discussion groups. The students may need prompting to weigh up the advantages and disadvantages of Charu buying her fruit and vegetables at the cheapest time.
Charu’s decision about when to buy her ingredients is about managing price and availability risks. She will look at these risks and weigh up the advantages and the disadvantages of buying her ingredients at different times.
Reflective question
Financial understanding
The supply and demand of goods determines their prices. This means that if there is a large demand relative to supply, prices will rise. Conversely, if there is a low demand relative to supply, prices will fall.
So prices can move up or down because demand and supply are changing all the time. This is easily seen in the supermarket. For example, one week, kiwifruit will be selling for $1.99 kg (during picking season when export rejects are sold on the local market), then prices rise after the picking season and are around $4.00 kg, even though they are still export rejects! As another example, a puzzle that cost a lot 3 years ago when demand was high may now be cheap because most people have one and demand is low. Also, when the price was high, more businesses would want to make that type of puzzle to “cash in” on the high prices. This extra supply would have brought the price down. The unit cost of the puzzle would also have reduced because of the large scale of production.
The price of many goods and services go in cycles, known as market cycles. Fruit and vegetables are one example because their supply is dependent on the growing seasons. Historically, house prices have tended to go up and flatten out or marginally decrease in cycles of about 7 years. Trendy items such as new technology, label fashion, and toys are also cyclic.
Increased supply often results in lower per-unit production costs because of mass production; the cost of producing commonly used technology such as cellphones or computers is a good example of “economies of scale”.
Social Sciences Links
Achievement objective:
• Understand how producers and consumers exercise their rights and meet their responsibilities (Social Studies, level 4)
Have the students discuss who the producers and consumers are in this activity, what some of their rights and responsibilities are, and how these impact on each other. (For example, quality of product: if the quality is poor, this will have flow-on impacts on Charu’s business.)
Answers to Activities
Activity One (page 2)
1. a. $634.50
b. Answers will vary. For example, signage, a till or money box, transport to shops, a stall or tent to sell from, wrapping for jars, plastic bags for customers, bank account fees
c. Answers will vary. For example, she might be able to buy some of the equipment secondhand.
2. a. $49. (0.07 x $700)
b. $62.42 per month for 11 months, with a final payment of $62.38; or $62.40 per month for 11 months, with a final payment of $62.60; ($749 ÷ 12)
c. Answers will vary. She could be trying to keep her outgoings lower while she is getting established (although she would end up paying more interest overall).
3. a. Definitions may vary.
i. Unpaid balance: the amount remaining on a loan at particular point before or after interest is added or repayments subtracted.
ii. Interest portion: the part of the repayment that the bank charges you for lending you the money.
iii. Principal portion: the part of the repayment that you are paying back from the amount you borrowed.
b. The interest portions get lower and the principal portions get higher. This happens because every month the interest is charged on the remaining balance, which gets lower and lower. Her monthly payment stays the same, so more gets paid off the principal.
4. Fair and Square Finance (12 x $62.20 – $0.07 = $746.33 or [11 x $62.20] + [1 x $62.13] = $746.33).
Over a year, Charu would pay $2.67 more to Credit Services ($749). With Fair and Square Finance, Charu could also pay off the loan faster and therefore reduce the amount of interest.
5. Answers and scenarios will vary. For example, if Charu borrows $700 from Grandad and pays him at least $62.20 a month for the first 6 months
and the rest over no more than 6 months at 15% per annum, she will be better off than if she borrows from the loan companies, as shown in the spreadsheet below. Note that the spreadsheet works on unrounded numbers but shows as (rounded) currency.
In this scenario, Charu has paid back $373.20 by the end of the first 6 months ($700 – $326.80 = $373.20). $373.20 + $340.23 = $713.43.
The following table compares the three loans:
So Grandad would be cheaper than Credit Services by $35.57 and cheaper than Fair and Square by $32.90. Note that this is only one scenario. For example, the more Charu pays Grandad back during the first 6 months, the less she will have to pay interest on after that. But if she tries to pay it back fast to save interest, she may not have enough money for other parts of her business. (The same applies to repayments to Fair and Square.)
Activity Two (page 4)
1. a. 140. (70 to get the $5 x 70 = $350 and 70 for her half later)
b. i. At least 71 shares
ii. Basically, Charu wants to stay in charge of the company. If all the other shareholders banded together to vote for a change, Charu would have the final say if she owned 51% but not if she owned 50% or less.
2. a. No. Kavi wants 20 shares ($5 x 20), Salila wants 28 (1/5), Tungar wants 15, and Ms O’Connor wants 14. That’s 77 shares altogether, which is 8 more
than there are available.
b. Answers will vary. There are many ways to split the shareholding, but Charu may decide to give each person two fewer shares than they want. That is, 18 for Kavi, 26 for Salila, 13 for Tungar, and 12 for Ms O’Connor.
c. Answers will vary, depending on your answer for question 2b above. For example:
3. a. $1.20. ($28 x 6 = $168 total profit. $168 ÷ 140 = $1.20 profit per share)
b. i. 24%
ii. Yes, 24% is a good return, much higher than the interest earned on deposits or investments in banks. Many shares return up to 10% per annum.
4. a. Based on the example in question 2b:
b. The percentage drops. Each person now gets an 18% net (after tax) return from their shares.
Reflective question
If Charu doesn’t make a profit, her shareholders won’t get any dividends. The value of the company’s shares may drop (because prospective shareholders may realise the future dividends could be low). So if any shareholders decide to sell their shares, they may get less than they paid for them.
Activity Three (page 7)
1. a. Freddie’s Fruitery ($119.00). ($7 cheaper than Violet’s Veges and $5.50 cheaper than Petra’s Pantry)
b. She would save $2 if she bought her cauliflowers and cucumbers at Petra’s Pantry and the rest at Freddie’s Fruitery ($35 + $18 + $50 + $8 + $6).
c. Answers may vary. She would have to visit two of the three shops and would use more time (and petrol, unless Petra’s Pantry is on the way to Freddie’s Fruitery) than if she shopped at just Freddie’s Fruitery.
2. a. March and April, although Charu will need to take into account the rising price of tomatoes in April and the fact that apples cost more in March than in April.
b. Apple chutney, between mid-April and early August
c. Answers will vary. For example:
i. Basically good thinking, based on price, but February and early May are also possibilities.
ii. It depends on whether people want to buy chutney between August and November. They might prefer to buy earlier in the winter. Charu may be able to sell at a higher price between August and November because people wouldn’t be making their own. Shewill need to keep accurate records and reassess for the following year.
iii. It depends on whether the bulk price was much cheaper than the 5 or 10 kg price.
Onions do eventually sprout and could be wasted.
Reflective Questions
Answers will vary.
• Prices of goods and services can change depending on the availability of the raw materials, the products themselves, or the time of year, which can affect
demand.
• Prices can rise or fall depending on the season and the quantity available for sale.
• Prices of products or services that depend on the time of year usually do go in cycles.