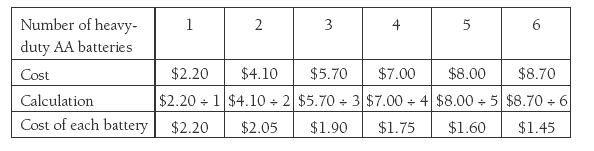This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (287 KB)
find fractions of money amounts
add money amounts
Number Framework Links
Use this activity to:
• help the students who are beginning to use advanced additive strategies (stage 6) to become confident at this stage in the operational domains of addition and subtraction and proportions and ratios
• encourage transition from advanced additive strategies (stage 6) to advanced multiplicative strategies (stage 7). (Use question 2 for this.)
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book One, Buying Batteries, page 16
This activity helps students to develop strategies for tackling simple fraction and proportion problems. Introduce it through a guided teaching group rather than as an independent activity unless your students are confident at stage 7 or above on the Number Framework.
Begin with some exercises to check that the students understand how to add using money notation. Then focus on why John chose to split $9.70 the way he did. If necessary, suggest that this made the problem easier for him to solve mentally.
When the students have completed question 1, ask them to suggest a different way to split $9.70. Ideas may include $10 – 30c or $8 + $1 + 60c + 10c.
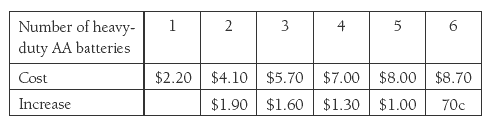
The students may find explaining the pattern in question 2 a challenge. They should be able to calculate the increase as the number of batteries grows:
Hints like What is happening as John adds another battery? may help them see that each additional battery is another 30 cents cheaper.
A more challenging way to look at the changes would be to have the students calculate the value of each battery in the pack as the number increases. This is a unit rate idea.
This pattern shows that the cost of each battery is reduced by 15 cents as one more battery is added.
The students who need to use materials to calculate each part of the pattern could draw large outlines of the batteries and use play money to distribute the price of each pack evenly among all the batteries.
To use number properties, the students will need to be able to divide or multiply. They could record their thinking as an equation, for example, $5.70 ÷ 3 = or x 3 = $5.70. You could make the problem accessible to advanced counting and early additive students by allowing them to use a calculator.
For questions 2b and 2c, the students will need to understand that John’s biggest pack is a 6-pack, so combinations will need to be tried and tested. Encourage the students to notice that the solutions involve using as many 6-packs as possible and have them try to explain why this is true. (6-packs have the lowest unit cost.)
Answers to Activity
Activity
1. a. $3.75. ( 1/2 of $7.00 is $3.50, and 1/2 of 50c is 25c. $3.50 + 25c = $3.75)
b. $12.75. (1/2 of $24.00 is $12.00, 1/2 of $1 is 50c, and 1/2 of 50c is 25c.
$12.00 + 50c + 25c = $12.75)
2. a. Answers may vary. The price of each extra battery goes down by 30c as the pack gets bigger. (The first extra battery costs $1.90, the second $1.60, and so on.) Or: The price of each battery in a pack is 15c cheaper than the price of the batteries in the previous pack.
b. A 6-pack ($8.70) + a 2-pack ($4.10)
c. i. A 6-pack and a 4-pack. ($15.70)
ii. Two 6-packs and a 3-pack. ($23.10)
iii. Three 6-packs and a 2-pack. ($30.20)