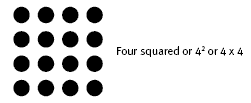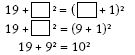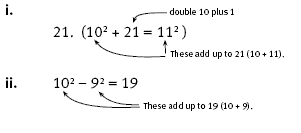Building Squares

Square numbers are one type of polygonal number. They are called square numbers because when a pattern of evenly spaced dots is drawn to represent that number, the dots form a perfect square. This activity will enable students to investigate the square pattern and become familiar with how squares can be represented using exponents. For example, the “²” is always used to mean squared.

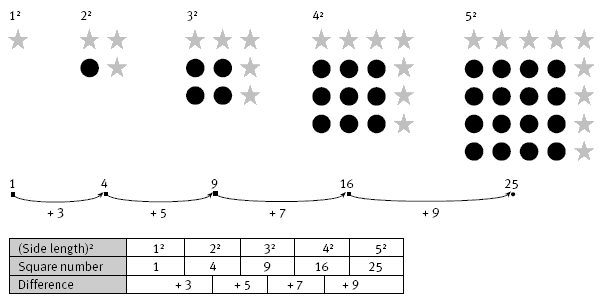
By building patterns with counters or square tiles or by shading squares up to 52 on grid paper, the students should be able to see a pattern developing. They can extend the sequence by building onto a smaller square to create the next largest square. They will thereby see that each larger square is formed by adding two side lengths and one more to the previous square total.

To look at the bigger picture in question 2, a table would be useful alongside the models.

In question 3, encourage your students to use additive and multiplicative strategies as they think out their answers.
Question 3a i can be reasoned using the formula “add two sides and one more to the previous square total”, for example, 10² + (10 x 2 + 1) = 112, or from the progression of odd-numbered differences (3, 5, 7, … 21).
For question 3a ii, the students could look for two consecutive numbers that total 19. However, you could encourage the students to look at it in terms of a similar patterning response to question 3a i or to use the additive inverse to subtraction. You could ask: “What square number added to 19 will give the next highest square number in this sequence?” and so on.

The inverse of this is 10² – 9² = 19.
Encourage students who wish to extend this investigation further to look for other patterns in consecutive square numbers. For example, they could observe that the square numbers alternate between even and odd.
You could ask them questions such as:
“Is there a pattern in the ones digits?”
“Are there more square numbers in the second hundred (101–200) than in the first hundred (1–100)?”
“What patterns can you find between consecutive triangular numbers?” (1, 3, 6, 10, …)
“What triangular numbers can you combine to make square numbers?” (For  example, 3 + 6 = 9)

Answers to Activity

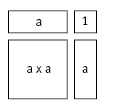
1. a. 2² is known as “two squared” because it gives the area of a square with sides of two units:

b. 7. (To make a 4 x 4 square, 16 tiles will be needed altogether.)
2. a. Practical activity
b. The differences are consecutive odd numbers (+ 3, + 5, + 7, + 9, …) or double the side length of each square plus 1.
3. a..

(When you subtract a perfect square from the next largest perfect square, the answer is the sum of the two numbers.)
b. i. Answers will vary. You can show 3² + 7 = 4² as You can also show this as

You can show this as a diagram. To build the next biggest square from a x a (a²):

you need to add two lengths of the current side length plus 1. That explains why the
differences are odd.
ii. Answers will vary. The simplest explanation, following the pattern shown, is to look for two consecutive numbers that add up to the solution.