This problem solving activity has a measurement focus.
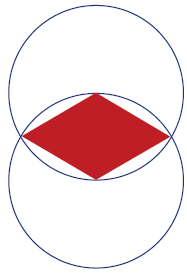
The centre of one circle lies on the circumference of the other.
Both circles have the same radius.
Use ruler and compass to draw your own copy of Bill’s Badge.
Bill uses a radius of 10cm for his circles.
What is the area of the red piece?
- Construct two intersecting circles where the radius of the second circle is on the circumference of the first.
- Use Pythagoras’ theorem to find the area of a rhombus.
- Devise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram, use a model).
In this problem students apply their knowledge of circles to a construction task. They should understand the significance of the two centres being on the two circumferences and know how to construct a rhombus.
As they work on the problem, students may notice that the two triangles formed by joining the centres of the circles, are equilateral. They may also approach the problem by applying their knowledge of Pythagoras’ theorem, or by using trigonometric ratios.
A similar problem is: Dan’s Badge, Measurement, Level 6.
The Problem
Bill is making a badge. He uses a ruler and a compass, and he colours it red and white. His drawing is below.
The centre of one circle lies on the circumference of the other. Both circles have the same radius.
Use ruler and compass to draw your own copy of Bill’s Badge.
Bill uses a radius of 10cm for his circles. What is the area of the red piece?
Teaching Sequence
- Plan a way of capturing the interest of the students in the problem. For example: Draw a circle on the board and ask the students to tell you everything that they know about circles.
- Pose the problem to the class. Check that everyone understands what the problem is about before asking them to work on it individually (or in pairs).
- As the students construct the intersecting circles, circulate asking questions that focus on the construction:
What can you tell me about your two circles?
What is the length this (pointing)? How do you know?
What shape is formed in the centre? How do you know? - As the students move on to working out the area of the rhombus ask questions that focus their thinking on the area of triangles.
How are you working out the area?
How could you apply Pythagoras' theorem?
How do you work out the area of a triangle? Does that apply to all triangles?
How do you know the "height" of the triangle? - Ask the students to record their work so that it can be shared with the class.
- Share solutions.
Solution
Construction: Since both circles have the same radius, the centre of the second circle is anywhere on the circumference of the first circle. After drawing the first circle, place the point of the compass anywhere on the first circle and draw another circle with the same radius. This will give the two centres. The other two points are at the intersection of the two circles so it is just a matter of joining up the four points to make the rhombus.
Area: Draw in the two diagonals to form the figure below.
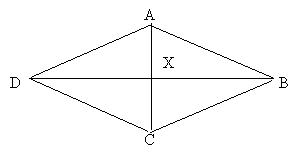
Then AC = 10 since AC is the radius of both circles. Hence AX = 5. Similarly AB = 10. Now the angle of AXD = 90 degrees, so we can find XD using Pythagoras.
XD2 = AX2 – AD2 = 102 – 52 = 100 – 25 = 75.
Hence XD = √75 = 5√3 ≈ 8.660
The area of the shaded figure is:
= 4 x the area of triangle AXD
= 4 (half base times altitude)
= 4( 0.5 x 5√3 x 5)
= 50√3
≈86.6 cm 2