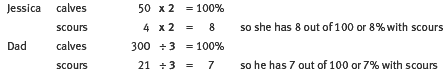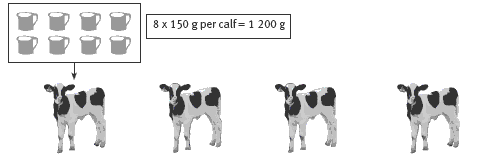This is a level 4 number, algebra and statistics activity from the Figure It Out series.
A PDF of the student activity is included.
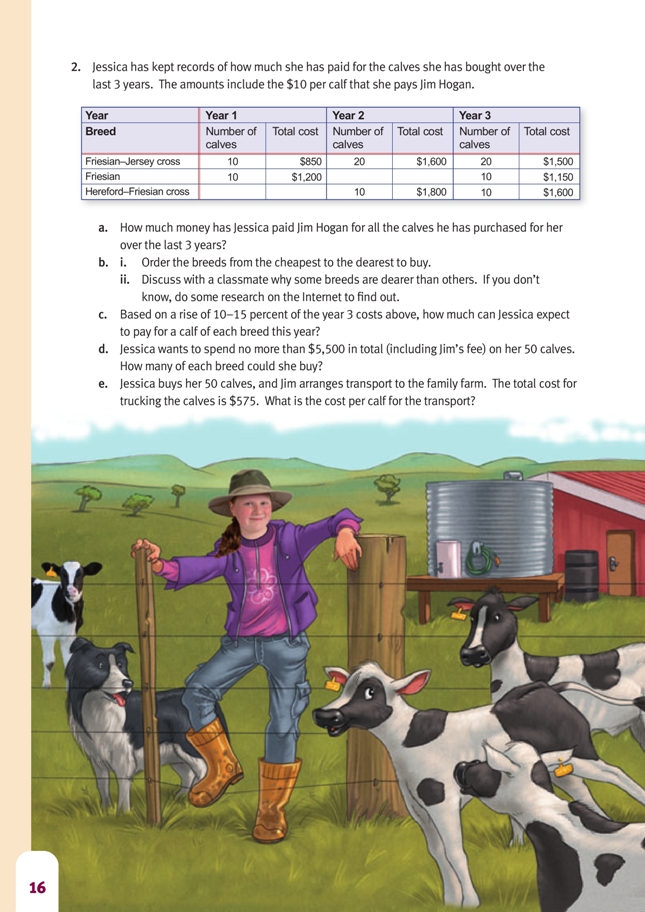
Click on the image to enlarge it. Click again to close. Download PDF (1681 KB)
use addition to sovle money problems
use multiplication and division to solve problems
find percentage of a number
solve problems involving ratios
find fraction of a number
Number Framework Links
Students undertaking this activity need to be at stage 7 or better. They will be required to solve problems involving percentages and metric conversions, so they will need to have a reasonable understanding of equivalent fractions. Knowledge of how to use a computer spreadsheet, including entering formulae, is important.
Internet access (optional)
FIO, Level 4-4+,Financial Literacy: Young Entrepreneurs, Beefing Up Business, pages 15-18
Calculator
A classmate
Context
For rural students, the raising of lambs and calves will be very familiar. City students may need some background information about raising calves to help them in interpreting the context. Calf raising is basically about taking 3-day-old calves and raising them until they are weaned and able to survive on grass, water, and
perhaps meal for food. The calves are then on-sold to beef farms that raise them until they are mature or to dairy farms as potential milk cows. Some dairy farms do their own calf raising, sometimes on blocks called “run-offs” dedicated to the purpose.
Students who are unfamiliar with the context may struggle to come up with reasons why the price of calves might fluctuate from year to year. You can help them with this by connecting Jessica’s scenario to the earlier scenarios in the book where price was determined by supply and demand. Ask the students to hypothesise why these might vary in respect to calves. The supply of calves depends mostly on the fertility of cows and the interest of dairy farmers in having calves born. Poor weather can reduce fertility, and poor forecasts of the price for calves can reduce farmers’ interest in producing them. Demand for calves is also determined by weather and projections of prices. Dry winters and springs can mean that feed on the farm will be short. This
also affects the ability of beef-raising farms to take on stock and lowers the demand for 4-month-old calves. For many potential calf rearers, particularly small-volume businesses, poor projections of returns mean the returns do not justify the risks and work required. The price of different breeds of calves is dependent on demand. Some breeds, like Herefords, are more popular because of their superior potential as beef cattle.
Financial language
The following financial terms occur during the story:
Agent/broker: A person who arranges exchanges of goods and services for a fee
Savings: The money people put aside from their income for future needs
Percentages: Fractions out of 100 that are commonly used to compare and to scale amounts, for example, comparing shooting statistics in sport or interest rates on savings
Profit: The amount of money left over from sales once the costs of producing the goods and services are met
Loss: The opposite of profit: the shortfall in money when a business’s costs are higher than its revenue (money made from sales)
Spreadsheet: A computer ledger used to keep financial accounts and other calculations
Account: A contract with a bank to hold or borrow money
Balance: The amount of money either in an account or borrowed from it (negative balance)
Trends and patterns: Happenings over time that allow future events to be predicted, for example, prices of stock
Investment: Savings or the purchase of an asset with the hope of future returns, for example, buying a rental property or business.
Financial understanding
Jessica’s goals show that she is becoming financially responsible. She understands that her decisions now will impact on her future choices. By earning income and saving now, she will be able to finance her own learning at university. Jessica is also demonstrating business understanding and financial maturity as she investigates the financial side of her business.
Jessica is matching her personal goals and capabilities to an undertaking. She demonstrates initiative and drive by running this business to earn money to pay for her university study, thus taking responsibility for managing herself. She uses the opportunities available to her through her farming background, including the use of facilities and the advice and expertise of her parents and her stock agent. She plans
her transactions carefully, particularly monitoring her cash flow and managing resources so that she can raise the greatest number of calves possible for her. She works in a small team with her father and communicates effectively with him to identify and solve potential problems.
Activity
Mathematics and statistics
To calculate the answers to question 2c, students need to calculate a percentage of an amount. For example, the price of a Friesian calf in year 3, including the agent’s fee, was $115 ($1,150 ÷ 10). Jim Hogan projects that prices will be 10 to 15 percent higher. Important knowledge for students is that percentage means “out of one hundred”, so the 10 or 15 is applied to every 100 dollars. Ten out of 100 is
one-tenth, so 10 percent of $115 is one-tenth of $115. Division by 10 is also a critical idea here. The effect of dividing by 10 can be shown on a calculator by keying in 1150 ÷ 10 = = = (some calculators may require ÷ 10 to be repeated). The resulting number has digits shifted one place to the right.
Using this idea, 10 percent of $115 can be calculated as $115 ÷ 10 = $11.50. Since 5 percent is half of 10 percent, 5 percent of $115 is half of $11.50 = $5.75. Another important idea is that the calf prices in year 4 will be between 110 percent and 115 percent of the year 3 prices. Percentages of the same amount can be added, so 115 percent of something is 100% + 10% + 5% of that something. This process can be
shown on a double number line as shown below:
With these representations, students should be able to calculate the potential prices for calves in year 4. Question 2d requires them to budget for purchasing 50 calves for no more than $5,500. Important questions you might ask the students include:
What will the average price per calf be? That is, the price if each calf cost the same, the middle price. $5,500 ÷ 50 = $110
What does that tell you about how many of each breed Jessica can buy? Friesian and Hereford–Friesian cross calves are dearer than this average, so a purchase of one of these must be balanced by purchasing Friesian–Jersey cross calves that are cheaper than the average. Jessica will need to buy more Friesian– Jersey cross calves to balance her budget.
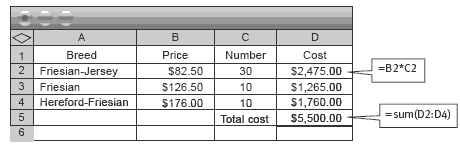
How might you use a table or spreadsheet to organise the possibilities to help meet the budget?
A spreadsheet can be set up that allows you to try “if–then” scenarios.
Using this spreadsheet, different scenarios can be explored, such as increases in calf prices by 15 percent and buying different numbers of each breed.
Question 2e involves a rate problem, that is, a multiplicative relationship between two measures. In this case, the measures are cost, in dollars, and number of calves. Most proportional reasoning problems like this can be represented by double number lines. This visual representation helps students to summarise the conditions of the problem and solve it using progressive steps. A double number line for 2e is given below.
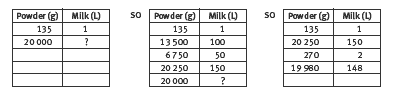
Some students are likely to need support in determining how to structure the operations to solve the problems in question 3. Diagrammatic support can help. Question 3a is a rate problem and can therefore be represented using a double number line or ratio table. The rate involved is between litres of milk and
kilograms of powder. Students will need to use the metric conversion: 1 kilogram equals 1 000 grams (kilo means 1 000). As a ratio table, the problem can be represented progressively as:
The problem can be solved efficiently by dividing 20 000 grams by 135 grams, the unit rate, that is, 1 litre : 135 grams. However, as both ratio tables and double number lines allow students to express the problem even if they are unsure of a strategy, they can make progress without using division. The students’ strategies are also more likely to involve mental calculation rather than rote procedures.
Question 4 involves comparison of two fractions as percentages. It is common to express two or more fractions as equivalent fractions with a denominator of 100, otherwise known as percentages. Both Jessica’s and her father’s scours rates are easily determined by a scaling operation.
This can also be expressed as fractions, as shown in the Answers:
4/50 = 8/100 21/300 = 7/100
Formulating the operations to perform is the biggest obstacle to students solving questions 4b and 4c. Encourage the students to draw diagrams if they need to think through which operations are involved. Examples might be:
So 4 x 6 = 24 or 4 x 8 = 32 litres per day.
Question 4c can be modelled in a similar way:
So 4 x 1 200 g = 4 800 grams = 4.8 kg (per day).
3 x 4.8 = 14.4 kg of powder over the 3 days.
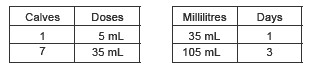
Question 5 also requires some knowledge of the metric system. One millilitre is one-thousandth of a litre. Five millilitres is about the contents of one level teaspoon. Question 5a is a double rate problem that relates calves to doses and millilitres to days. As such, it can be modelled by a ratio table:
So Jessica is 5 millilitres of penicillin short. If 100 millilitres cost $26.00, then 5 millilitres is one-twentieth of that because 20 x 5 mL = 100 mL. $26.00 ÷ 20 can be performed mentally in a number of ways:
$26 ÷ 10 = $2.60, $2.60 ÷ 2 = $1.30; or $26 ÷ 2 = $13, $13 ÷ 10 = $1.30; or $1.00 ÷ 20 = $0.05 (5 Cents), so $26.00 ÷ 20 = $26 x $0.05 = $1.30.
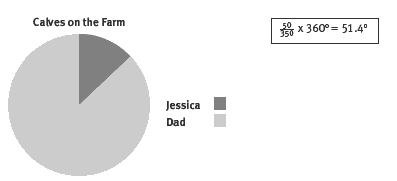
Question 6 involves expressing a ratio of fraction terms. To do that, it is important to identify the parts and the whole.
The ratio of calves is 50:300 (Jessica’s to Dad’s). So diagrammatically, the herd of calves looks like this:
So Jessica’s fraction of the whole herd is one-seventh (not one-sixth, as is the common error). As well as feeding her own calves, Jessica should probably help her father feed his calves in return for her use of the farm facilities. The degree of compensation is discretionary, but the students might want to consider on
which days of the week Jessica might be more able to help her father. For example, apart from holidays, Monday to Friday are school days (and she still will have to feed her own calves on those days), so it may be easier for her to help on the weekends.
Social Sciences Links
Achievement objectives:
• Understand how producers and consumers exercise their rights and meet their responsibilities (Social Studies, level 4)
• Understand how people seek and have sought economic growth through business, enterprise, and innovation (Social Studies, level 5)
Have the students discuss:
– How is Jessica seeking economic growth?
– What flow-on economic growth impacts will Jessica’s enterprise have?