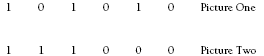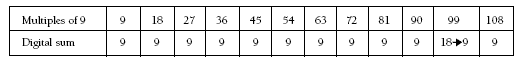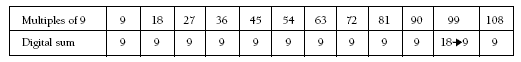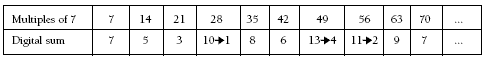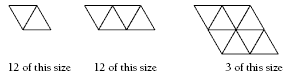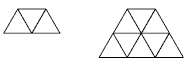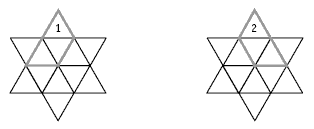These are level 3 number, algebra, and geometry problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (274 KB)
explore patterns in mutliples of 7, 8, 9 multiplication facts (Problem 2)
identify parallelograms and trapeziums in geometric shapes (Problem 3)
explore the idea of equality in diagrams of scale balances (Problem 4)
Problem One
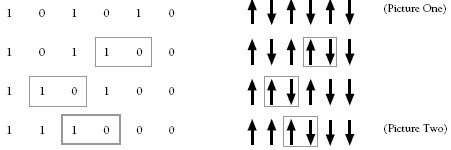
This problem can be likened to switches being open or closed. The early evelopment of computers involved binary reasoning. Binary in this case means that only two possibilities exist: an arrow can be either up or down.
If binary numbers were used, 1 for up and 0 for down, the problem would look like this:
This representation may make the problem easier for students who get confused with all the arrows. Another method is to put the arrows onto cards so that they can be moved. Here is one way of solving the problem:
Students should be able to apply similar logic to find out how many adjacent arrow turns are needed to change
into
Problem Two
The digital sums of multiples produce fascinating patterns.
In the case of multiples of nine, the pattern is:
Ask students to explain why the digit sum for the first 10 multiples of nine is 9. They may notice that, because 9 is one less than 10, each addition of 9 (obviously up to 90) results in the tens digit increasing by one but also the ones digit decreasing by one.
With multiples of eight, we would expect that the ones digit will decrease by two and the tens digit will increase by one with each addition of eight. The digital sum should therefore decrease by one with each successive multiple.
The principle of digits increasing and decreasing is based on the idea of clock arithmetic.
In special cases like 48, the rule appears to break down. After 40 (8 x 5), increasing the tens digit by one would give 5_ (50 something). Decreasing the ones digit by two on the clock would result in eight. To compensate for the minus two, we get 50 – 2 = 48.
Similarly, with multiples of seven, the tens digit increases by one and the ones digit decreases by three. With the 21 → 28 transition, 21 → 31 (tens digit up by one) minus three gives 28.
Students should now be able to anticipate the pattern for digital sums of multiples of six.
Problem Three
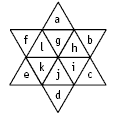
Students will need to know what parallelograms and trapezia are. A parallelogram is a four-sided polygon with two pairs of parallel sides. The shapes below are all parallelograms.
A trapezium is a four-sided polygon with only one pair of parallel sides. The shapes below are all trapezia.
Students will need to use a systematic approach to find all the parallelograms and trapezia in the figure. They will find three sizes of parallelograms:
There are only two sizes of trapezia.
To work out the number of , each corner triangle can be dealt with separately.
Two trapezia of this size are made using each corner triangle. This gives 6 x 2 = 12 in total.
Within the hexagon formed by the six internal triangles, there are six further trapezia of that size.
So there are 12 + 6 = 18 trapezia of the size ![]() .
.
Considering that two corner triangles each time must be used to make a large trapezium, there are six possibilities:
This gives a total of 18 + 6 = 24 trapezia.
A slow but thorough strategy is to label each triangle in the star and use the labels to name each shape as it is found.
A strategy for finding all the parallelograms is to start with all the parallelograms that involve triangle a, then b, and so on.
ag aghi aglk aghijdkl
bh bhij bhgl bhijkelg
ci cijk cihg cijkhglf
dj djkl djih
ek eklg ekji
fl flgh flkj
gh gl hi ij jk kl
Problem Four
There is a spotty bag on each side of the right-hand balance, so these could both be removed and the balance would be retained. Therefore one pink bag weighs the same as two blue bags.
Looking at the left-hand balance, if each pink bag were replaced with two blue bags, the balance would remain. This would mean that six blue bags weigh the same as two spotty bags. One spotty bag is therefore balanced by three blue bags.
Algebraically, the scales pictures could be represented as the equations 3p = 2s and s + p = 2b + s,
where p is the mass of a pink bag, s the mass of a spotty bag, and b the mass of a blue bag. We can remove a spotty bag from each side of the right-hand balance, so now we have:
3p = 2s and p = 2b
which can be simplified as 3 x 2b = 2s
6b = 2s
3b = s.
Answers to Problems
1. 3
2. a. In each case, the digits total 9.
b. The pattern is decreasing by 1. (When the single-digit number gets to 1, the next
number is 9 and the pattern continues.)
c. The pattern is groups of 4 odd or even digital sums decreasing by 2:
3. a. 27
b. 24
4. 3