These are level 3 x problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (181 KB)
find the area of a rectangle (Problem 1)
solve puzzles involving 3 dimensional drawings (Problem 2)
use addition to solve puzzles (Problem 3)
find outcomes using a diagram (Problem 4)
Problem One
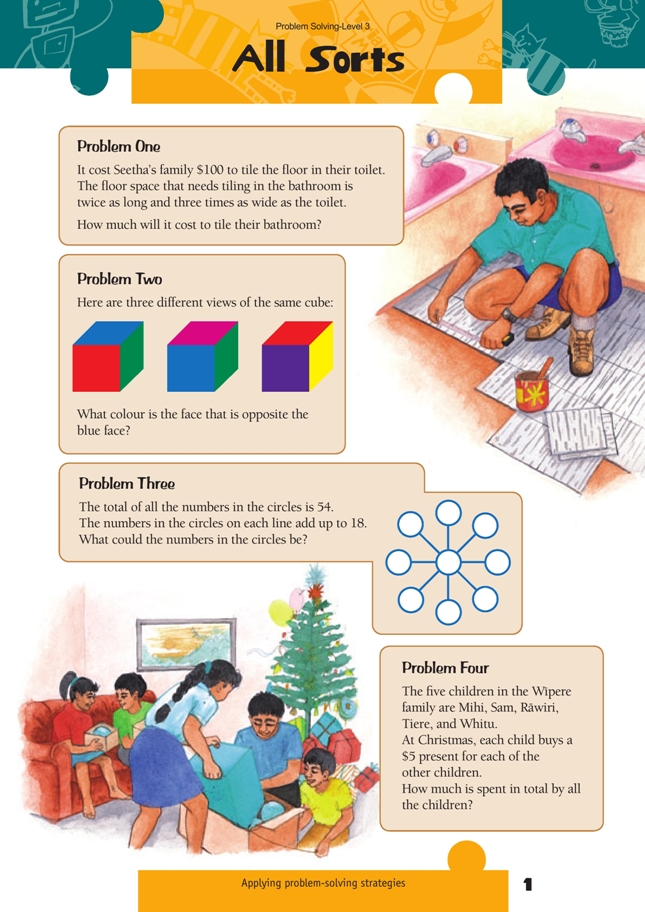
A physical model of the problem will help students to visualise the comparative area of the toilet and bathroom. Let one square tile represent the area of the toilet:
Therefore, the cost of tiling the bathroom is six times that of the toilet.
The problem can easily be extended by providing different dimensions for enlargement. For example, “The kitchen is twice the size of the bathroom. How much longer and wider could it be than the toilet?”
This would mean that the kitchen has 12 times the area of the toilet. A table is a good way to organise the possibilities:
More able students may realise that the dimensions need not be restricted to whole numbers. For example, the kitchen might be five times wider and 2.4 times longer than the toilet.
Problem Two
Three-dimensional problems like this are extremely difficult to solve unless some form of model is used. This may be a cube or the net for a cube. Following the pictorial clues and using coloured pens to shade the appropriate faces on the model make solving the problem easier.
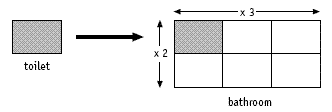
Another approach is to use a process of elimination. The left-hand view shows that neither red nor green can be opposite blue because they are adjacent to it. Similarly, the middle view shows that pink is also adjacent to blue. This leaves purple and yellow as the only possibilities left to be opposite blue.
If you roll the right-hand cube forward so that red is facing:
then make a quarter turn to the right:
you can see that the bottom face is purple and the face at the back is yellow. This means that the front face must be blue and the top face must be green. So yellow is opposite blue.
Students will enjoy creating their own cube puzzles for others to solve.
Problem Three
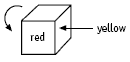
Finding out which number is in the centre circle is the most difficult part of the problem. Students may work this out by trial and improvement, or they may divide 54 (the total of all the numbers in the circle) by nine (the number of circles). This gives six, which is a good choice for the centre circle.
A more rigorous approach is to realise that each row of three circles adds to 18, so the total is 4 x 18 = 72. The circle numbers total 54, and the difference of 18 (72 – 54) is the result of the centre number being counted three extra times. So the centre number must be six.
Once this is established, students can find a large number of possible answers. The numbers on opposite ends of a line will always add to 12. For example:
Similar problems are easy to make by changing the conditions. For example, tell students the circle numbers add to 63 and each line of circle numbers adds to 21.
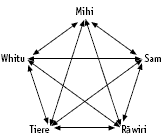
Problem Four
An important deduction is that each child in the Wìpere family will have four other children to buy for, so the total number of presents will be 5 x 4 = 20. Students may find this using a number of strategies.
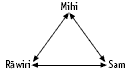
An arrow diagram is particularly useful, especially if students first use an arrow diagram to solve a simpler problem, for example, fewer children in the family:
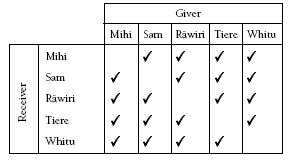
A matrix or table is useful when students assume the roles of the Wìpere children to act out the problem.
Encourage students to generalise by asking questions such as: “What if there were six children in the family?” “What about seven children?”
Another variation, which will lead to a set of triangular numbers, is “What if the children give a present only to brothers and sisters who are younger than them?” Students may want to know the age of the Wìpere children, though this is irrelevant. The oldest child will give four presents, the next oldest three presents, and so on. Only four children, not five, will give presents in this scenario because the youngest has no one to give a present to. The number of presents will be 4 + 3 + 2 + 1 = 10. If there were six children in the family, the number of presents would be 5 + 4 + 3 + 2 + 1 = 15.
Answers to Problems
1. $600
2. Yellow
3. Many answers are possible. The centre number must be 6. The 2 numbers at either end of each line must add to 12.
4. $100