This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
Click on the image to enlarge it. Click again to close. Download PDF (370 KB)
choose from a variety of mental strategies to solve problems
Number Framework Links
Use this activity to help your students consolidate and apply multiplicative part–whole strategies (stages 6–7) in the domain of multiplication and division.
FIO, Level 3, Multiplicative Thinking, Adventure Tokens, page 19
A classmate
This activity gives students opportunities to use a range of multiplicative strategies to solve rate problems involving multiplication and division. Students will need a reasonable knowledge of multiplication basic facts if they are to use multiplicative strategies rather than repeated addition.
If your students use repeated addition to solve the problems, encourage them to use multiplicative part–whole strategies by asking them to find alternative solution paths. Share strategies for each problem with the group and talk about which was most efficient.
Once students have acquired a range of part–whole strategies that they can use flexibly, it is important that they recognise which one would be most useful and efficient when faced with a particular problem situation. This activity provides opportunities to encourage this skill if used as a guided teaching session. Throughout the activity, ask questions such as:
- Before you start working out the problem, look at the numbers and decide which strategy is likely to be most efficient for this particular problem. Could you explain why to a classmate?
- Share your solution path with the group. Did someone else use a more efficient method? What is there about the problem that suggested the use of this strategy?
If students have difficulties using the one-third information to solve Naraini’s problem in question 1, ask:
- How many tokens has Naraini used having 6 rides on the roller coaster? (6 x 8 = 48 tokens)
- Draw a diagram that shows that Naraini has used one-third of her tokens and that this one-third is 48.
Possible diagrams could be: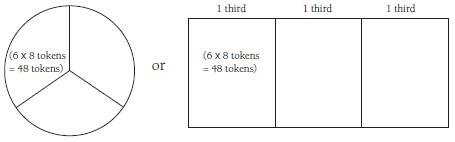
- If there are 48 tokens in one-third of the diagram, how many tokens are in the other two-thirds? (2 x 48 = 96)
Possible part–whole multiplicative strategies to explore and compare for 2 x 48 = ? include:
- using tidy numbers and compensating: 2 x 48 = (2 x 50) – (2 x 2) = 100 – 4 = 96
- using place value partitioning: 2 x 48 = (2 x 40) + (2 x 8) = 80 + 16 = 96
- doubling and halving: 2 x 48 = 4 x 24 = 8 x 12 = 96.
Possible solution paths to explore for question 2 are noted in the Answers.
Compare different solution paths for question 3, such as:
- 126 tokens ÷ 3 people = 42 tokens each; 42 tokens each ÷ the 7 tokens it costs to go on the dodgems = 6 rides each: 126 ÷ 3 = 42, 42 ÷ 7 = 6
- 126 tokens ÷ 7 token dodgem cost = 18 turns for 3 people; 18 turns ÷ 3 = 6 turns each: 126 ÷ 7 = 18, 18 ÷ 3 = 6
- 1 turn on the dodgems for 3 people costs 7 x 3 = 21 tokens. (? x 20) + (? x 1) = 120 + 6 = 126; ? = 6.
Possible part–whole multiplicative strategies to explore and compare include:
- 126 ÷ 3 = ?
– partitioning: 126 ÷ 3 = (120 ÷ 3) + (6 ÷ 3) = 40 + 2 = 42
– making proportional adjustments: 126 ÷ 3 = 2 x (63 ÷ 3) = 2 x 21 = 42 - 126 ÷ 7 = ?
– making proportional adjustments: (126 ÷ 7) = 2 x (63 ÷ 7) = 2 x 9 = 18
– using known facts and the distributive property: 70 ÷ 7 = 10, 126 – 70 = 56, 56 ÷ 7 = 8, 10 + 8 = 18.
There is only one solution for question 4 if Chloe is to use all her tokens. A possible solution path is to start with a guess and then work systematically to adjust the levels of tickets until exactly 50 tokens are spent. One way of doing this is to create two lists: one for the cost of trips on the river ride (6, 12, 18, …) and another for the cost of rides in the bumper boats (7, 14, 21, …). The students then see if they can pair 6 (12, 18, …) in the first list with a number in the second list that will make 50. Ask the students how they can be sure that their solution is the only one.
To ensure that the students don’t create problems without solutions in question 5, remind them that they must be able to solve their own problems and explain the solutions to others.
After the activity
Encourage reflective thinking by asking questions such as:
- Was there a strategy that you used today that you thought was particularly efficient for one of the problems?
- Did someone else share a solution path or strategy today that you might use if you were doing the same problem again? What was it about the problem that might tell you that this would be an efficient strategy?
Answers to Activity
1. a. 96 tokens left. (6 x 8 tokens = 48 tokens, which is one-third of her tokens. So she has two-thirds left:
2 x 48 = 2 x 50 – 4 = 96 tokens)
b. Answers will vary. One way is for Naraini to go on the dodgems 4 times (4 x 7 = 28), the river ride 6 times (6 x 6 = 36), and the merry-go-round 8 times (8 x 4 = 32). 28 + 36 + 32 = 30 + 36 + 30 = 3 x 30 + 6 = 96 tokens
2. 111 tokens. (Possible methods:
multiply each ride by 3: [3 x 4] + [3 x 5] + [3 x 6] + [3 x 7] + [3 x 7] + [3 x 8] = 111;
add up adjacent pairs of rides and multiply by 3: [3 x 9] + [3 x 13] + [3 x 15] = 111;
find tidy pairs and multiply by 3: [3 x 10] + [3 x 12] + [3 x 15] = 111;
add up all the token values and multiply by 3: 4 + 5 + 6 + 7 + 7 + 8 = 37; 37 x 3 = 111;
or add up in groups of 2 and multiply by 3: 9 + 13 + 15 = 37; 37 x 3 = 111)
3. 6 rides each. (Using multiplication: If the 3 friends all have 1 ride on the dodgems, this will cost them 3 x 7 = 21 tokens altogether. 21 x ? = 126; 21 x 6 = 126. Using division: 126 ÷ 3 = 42; 42 ÷ 7 = 6.)
4. 6 times on the river ride and 2 times on the bumper boats. (6 x 6) + (2 x 7) = 36 + 14 = 50
5. Problems will vary.
