This unit explores situations that involve addition and subtraction of whole numbers. Students are expected to choose among a range of strategies, based on their understanding of place value.
- Choose appropriate strategies such as using standard place value, using tidy numbers with compensation, and equal adjustments when solving addition and subtraction problems with whole numbers.
- Choose correct operations to solve joining, separating, and difference problems with whole numbers.
- Record solutions using equations, algorithms, and calculator inputs.
There are three types of situations to which addition and subtraction are applied.
- Joining parts to form a whole
Example: You have 35 toy cars and are given 47 more. How many cars do you have?
Equation: 35 + 47 = 82 - Separating parts from a whole
Example: You have 82 toy cars and give 47 away. How many cars do you have?
Equation: 82 - 47 = 35 - Comparing parts or comparing whole.
Example: You have 82 toy cars, and your friend has 35 toy cars. How many more cars do you have than her?
Equation: 35 + □ = 82 or 82 – 35 = □.
The role of the unknown changes the difficulty of the problem and the operation needed to solve it.
- Joining change unknown
Example: You have 35 toy cars and get some more cars. Now you have 82 cars. How many cars did you get?
Equation: 35 + □ = 82 - Separating start unknown
Example: You have some toy cars and give 47 cars to your friend. Now you have 35 cars. How many cars did you have to start with?
Equation: □ - 47 = 82 - Comparing start unknown
Example: You have 82 toy cars. That is 47 more cars than your friend. How many cars does your friend have?
Equation: □ + 47 = 82
Notice that the same equation can represent a range of different situations.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- providing place value materials so that students can anticipate actions and justify their solutions. Use materials like place value blocks, bundled iceblock sticks, and beaNZ in canisters that are proportional, e.g. ten ones comprise the tens unit. Physical representation diminishes the degree of abstraction required and helps students see what is occurring with the quantities that numbers represent
- connecting symbols and mathematical vocabulary, especially the symbols for addition and subtraction (+, -) and for equality (=). Explicitly model the correct use of equations and algorithms and discuss the meaning of the symbols in a relatable context
- altering the complexity of the numbers that are used. Using more places, e.g. three digits or two digits, tends to increase complexity though much depends on the renaming that is required. Addition tends to be easier than subtraction though that depends on the nature of the numbers.
- encouraging students to collaborate in small groups and to share, and justify, their ideas
- using technology, especially calculators, in predictive, pattern-based ways to estimate sums and differences, e.g. Is the answer to 83 – 47 closer to 20, 30, 40, or 50? How do you know? Allow use of calculators where you want students to focus more on the process of getting a reasonable answer than on practising calculation skills
- providing digital representations or addition and subtraction problems which students can use to demonstrate their thinking, manipulate groups of numbers, and share their strategies with others
- recording their explanation of how they solved the problems which, can be set up as a class exemplar for students to refer to for support
- using Talk Moves to enhance students’ understanding of the strategies and when it is best to use them.
The contexts used for this unit include occupations, finance, and collections of objects. Adjust the contexts to everyday situations that your students are likely to be interested in, and that reflect their cultural identities. Addition and subtraction problems can easily be framed in terms of objects that are meaningful to your students, such as natural objects (e.g. pine cones), people in their kura or whānau, or points earned in games or other competitions. Encourage students to be creative by accepting a variety of strategies from others and asking students to create their own problems for others to solve, in contexts that are meaningful.
Te reo Māori vocabulary terms such as hono (join), tango (subtract), huatango (difference in subtraction), whārite (equation) and manarite (equality) could be introduced in this unit and used throughout other mathematical learning.
- Proportional Place Value materials, for example, Place Value Blocks, BeaNZ in canisters, Iceblock sticks and rubber bands, Place Value People.
- Calculators
- Copymaster 1
- Copymaster 2
- Copymaster 3
- PowerPoint 1
Session One
Begin each session in this unit with an addition/subtraction grid. This session gives you details about how to introduce the activity. Grids for the other sessions are provided in PowerPoint 1. Try to limit this activity and discussion of how students found the answers to no more than ten minutes.
- Show Slide One of PowerPoint 1.
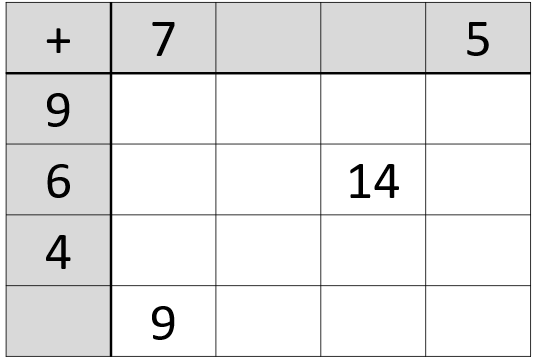
Discuss how to complete the grid. The answers to the additions go in the body of the table. For example, 7 + 6 = 13 so 13 can be placed in the second cell in the third row.
Some of the addends (numbers to add) are missing.
How will you workout what numbers they are?
Students might recognise that 2 goes in the bottom of the left-hand column because 7 + 2 = 9. Students check with a buddy that they both understand how to complete the grid. - Let students complete the grid. Some students enjoy the challenge of improving on their time from day to day, but others may not. Students can record their time each day if that motivates them.
Use the animation of Slide One (mouse clicks) to show the answers and how those answers can be determined from the information that is given. - The key idea in this lesson is to solve addition and subtraction problems using place value. Make sure that you have physical materials that represent the place value structure of whole numbers, such as Place Value Blocks, beaNZ in canisters, iceblock sticks in bundles, or Place Value People. Money is not a proportional representation, and one cent coins are no longer used. Use problem stories other than those involving money, if possible. A suitable problem could be:
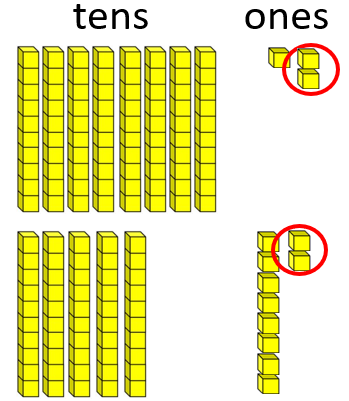
On her birthday all Aniwa wanted was her favourite seafood. She received 56 pipis in the morning and 37 kuku (mussels) in the afternoon. Because of the numbers she suspected that someone snuck a few for themselves before giving them to her. However, she was happy because she still had plenty to share with her whānau and friends. How many shellfish did she receive?
Represent each calculation using both the physical materials and empty number lines. For example, 56 + 37 = 93 can be represented as: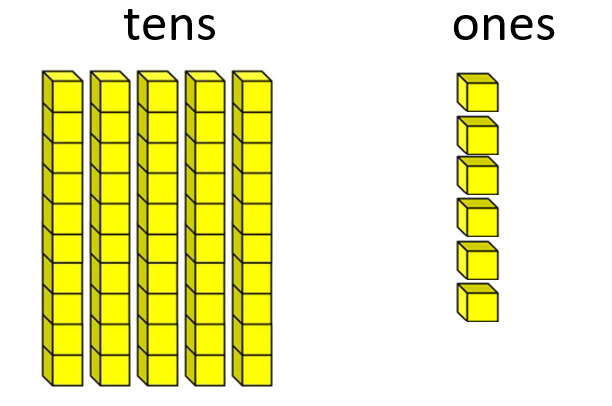
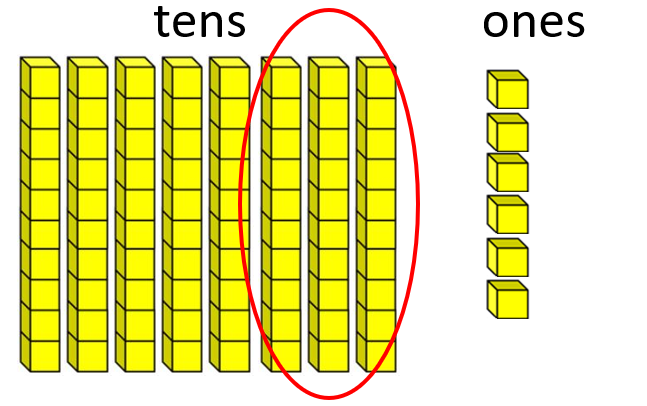
56 equals 5 tens, and 6 ones Adding 30 gives 86, 8 tens, and 6 ones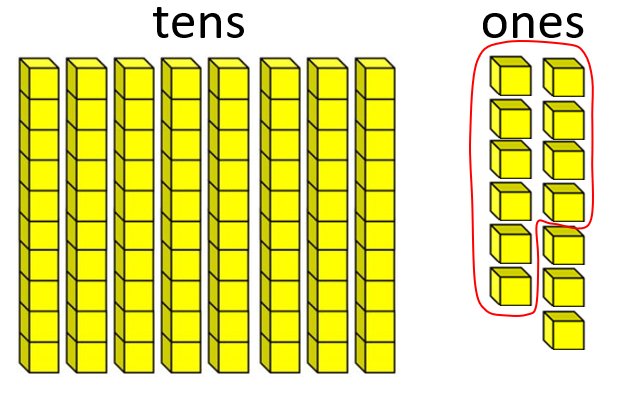
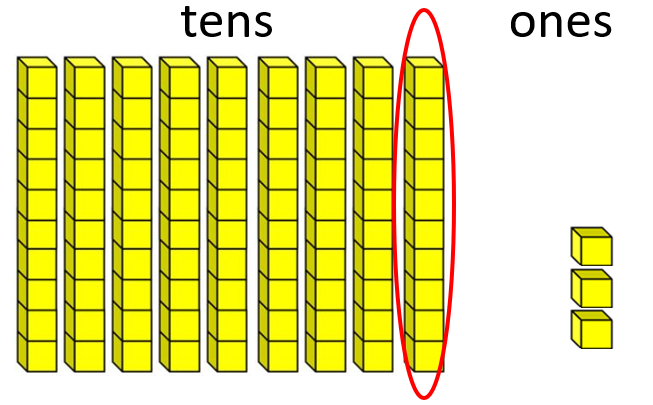
Adding 7 gives 8 tens, and 13 ones 10 ones make 1 ten so the answer equals 93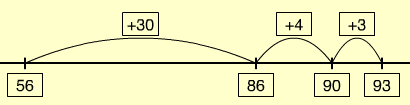
Another problem could be:
Korimako was organising his first local kapa haka festival. He was amazed at the number of groups that entered. There were 57 senior groups and 45 junior groups. How many groups registered altogether?
Session Two
- Use Slide Two of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
- The key idea in this session is using tidy numbers with compensation to solve addition and subtraction problems. Consider using proportional place value materials rather than money, and changing the contexts of the problems to be encouraging and relevant to your students.
- Pay particular attention to the inverse compensation needed for subtraction.
For example, consider 72 – 38 = □ (in an appropriate story context). An example could be: John had 72 marbles but over two weeks he lost 38 marbles to his friends. How many does he have now?
With place value blocks the problem might be represented as: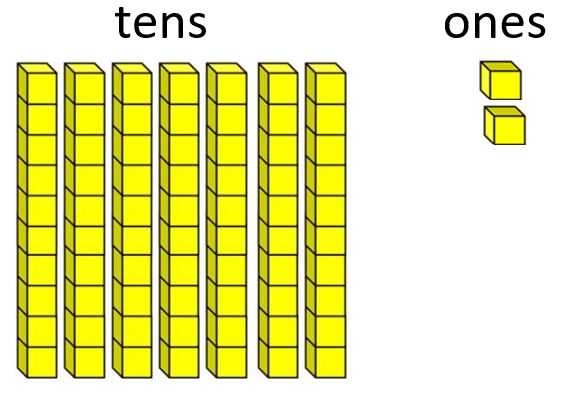
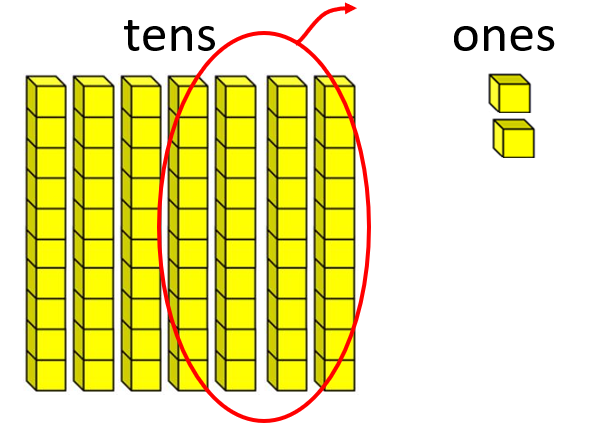
72 equals 7 tens, and 2 ones Subtract 40 (4 tens) leaves 3 tens, and 2 ones (32)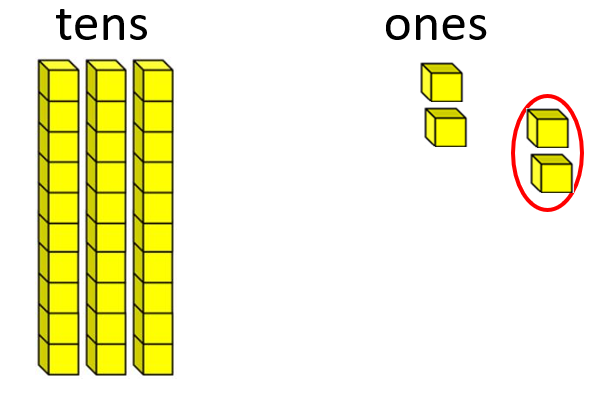
Compensating for removing 40 instead of 38 gives 3 tens and 4 ones (34)
The same operation on an empty number line looks like this: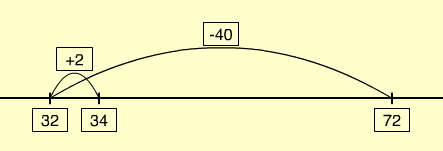
- Pose problems with three-digit whole numbers as well, such as:
There are 725 trout in Lake Kahurangi at the start of the fishing season.
297 of the trout are caught.
How many trout are left? - Let students practise from Copymaster 1. Ask students to share their strategy with a partner.
Session Three
- Use Slide Three of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
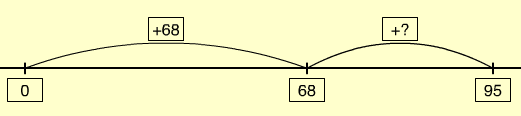
- The key idea in this session is about using the inverse relationship between addition and subtraction, particularly solving subtraction problems by adding on. Use proportional place value materials rather than money. Use problems with contexts that are of interest to your students.
- It is important that students understand why it is possible to solve a problem like 95 – 68 = □ by solving 68 + □ = 95, as well as developing the procedural fluency in doing so.
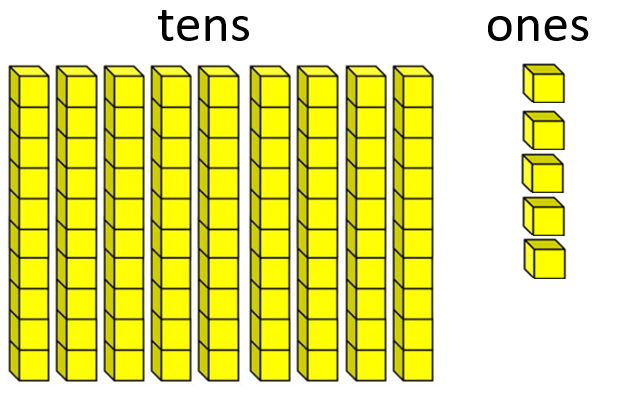
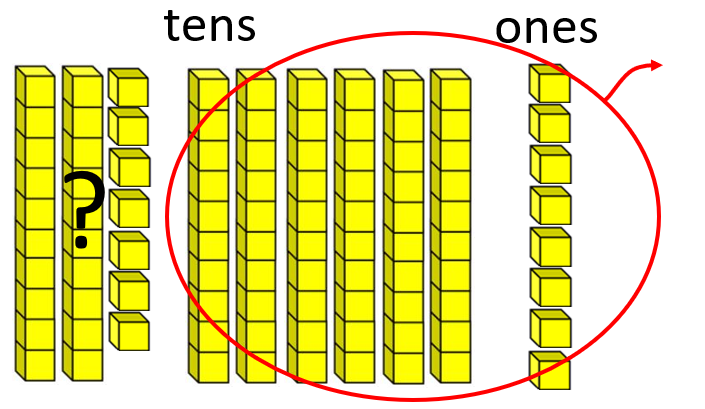
95 equals 9 tens and 5 ones If 68 was subtracted there would be ? left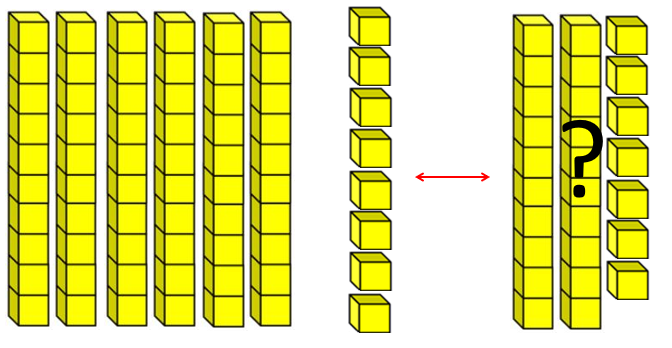
That means 68 + ? = 95
In empty number line form the problem is represented like this: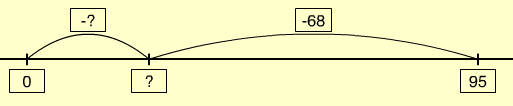
- Let students practise from Copymaster 2 and share their thinking with a partner.
Session Four
- Use Slide Four of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
- The key idea for session 4 is about students making sensible strategic choices about how to solve addition and subtraction problems. Encourage students to use mental and written methods. Only use proportional place value materials when students need additional support. Change the contexts of the problems to be about items that are of interest to your students. Ask the students to provide contexts also.
- Discuss the criteria for deciding which method/s are the best for certain calculations. Encourage students to make up problems that each strategy (place value, tidy numbers, inverse thinking) would be useful for.They might conclude:
- Place value works on any numbers but is more difficult where renaming is required.
- Tidy number strategies work best when the one or both numbers are close to a tidy number (usually a decade or century).
- Inverse thinking strategies work on any numbers but are especially useful if renaming is needed for subtraction.
- Equal adjustment is another strategy where the addition form of equal adjustment is conceptually easy, but the subtraction is not. Choose whether, or not, to offer those strategies to your students but do not invest too much time in doing so. Here are examples:
- Addition 48 + 34 = □
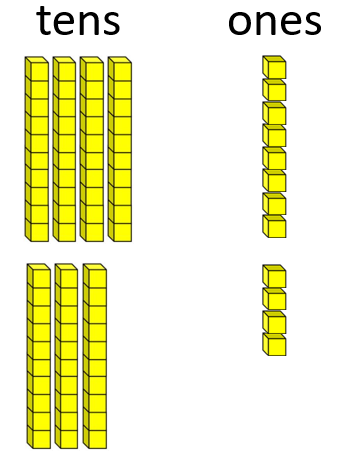
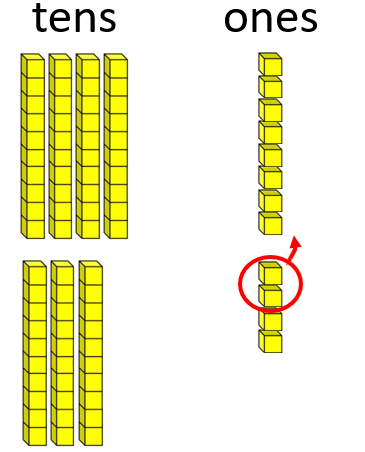
48 add 34 has the same sum as 40 + 32 = 72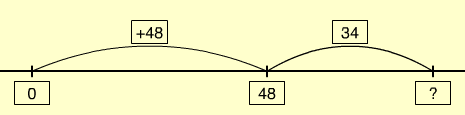
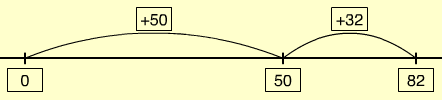
- Subtraction 81 -58 = □
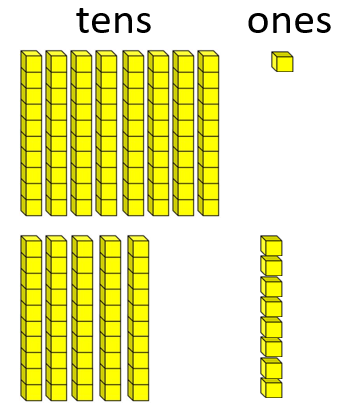
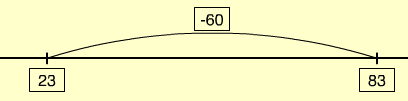
The difference between 81 and 58 is the same as the difference between 83 and 60.
83-60 = 23.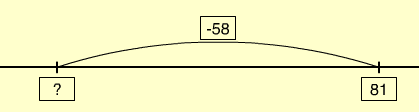
- Addition 48 + 34 = □
- To practise applying addition and subtraction strategies ask students to work on these Figure It Out activities:
- Tidying Up, from Number Sense and Algebraic Thinking, Level 3, Pages 2-4,
- The Strategy Strut, from Number, Level 3, Book 3, Pages 6-7,
- Another useful strategy is to split the smaller number into tens and ones. For example 81 - 58 becomes 81 - 50 - 8. 81 - 50 is 31 and 31 - 8 is 23 so 81 - 58 = 23
Session Five
- Use Slide Five of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
- In this session, the key idea involves use of standard written forms for addition and subtraction. Students should also use calculators as another way to find answers to addition and subtraction problems. When solving problems use the simplest written form for addition rather than the expanded form.
- Use proportional place value materials when developing the written forms so students understand what is occurring with the quantities. Alongside learning for understanding give students sufficient practice to develop fluency. Here are examples:
- Addition
- Subtraction (using decomposition)
- Addition
- Let students practise from Copymaster 3.
Dear parents and whānau,
In mathematics this week, our focus is on solving problems with addition and subtraction. We will learn several different strategies including working out answers in our head, on paper, and using a calculator. We are encouraging the development of in-depth mathematical understanding rather than rote learning. As students develop their efficient use of one or two addition and subtraction strategies, the speed at which they operate on different numbers will increase.
At the end of the week you might give your child a problem to solve, such as 38 + 62 or 73 – 26 and ask them to explain their preferred way to solve it and why they chose that way. When you went to school you may have learned a different method. Talk to your student about how your method works.