New Zealand Curriculum: Level 3-4
Learning Progression Frameworks: Multiplicative thinking, Signpost 6 to Signpost 7
Target students
These activities are intended for students who understand multiplication and division of whole numbers and who know most, if not all, of the basic multiplication facts. It is also expected that students have an existing understanding of whole number place value, to at least six places.
The following diagnostic questions indicate students’ understanding of, and ability to apply, decimal place value. The questions are given in order of complexity. If the student answers a question confidently and with understanding proceed to the next question. If not, use the supporting activities to build and strengthen their fluency and understanding. Allow access to pencils and paper but restrict calculator use to the questions that require it. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them.
- Order these measurements by their length, shortest to longest.
2.6 metres 2.59 metres 2.487 metres
Signs of fluency and understanding:
Orders the measures as 2.487, 2.59, 2.6
When prompted, uses place value to justify their comparisons.
What to notice if your student does not solve the problem fluently:
Ordering the numbers as 2.6, 2.59, 2.487 may indicate that the students applies whole number thinking to decimals, such as "59 is greater than 6 so 2.59 is greater than 2.6".
Ordering the numbers as 2.487, 2.59, 2.6 may indicate that the student applies reciprocal or ‘longer is smaller’ thinking, such as "decimal values get smaller, the more digits the number has.”
Supporting activity:
Ordering decimals
- Here is a number line that has zero and two marked on it.
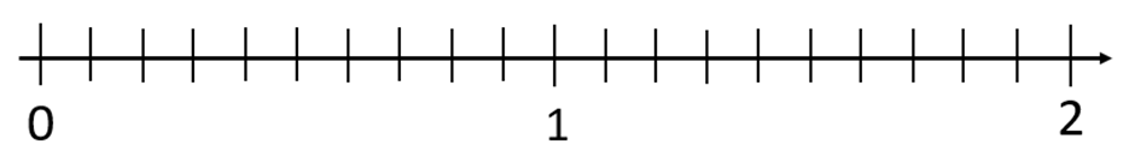
Mark where each decimal goes on the number line and write the decimal underneath the mark.
0.4m 1.2m 0.75 1.95 0.333
Signs of fluency and understanding:
Locates the decimals correctly with reasonable attendance to scale. For example, 0.4 should be less than one half, preferably located at four tenths. 0.75 should be half-way between 0.7 and 0.8, so three quarters of the length between 0 and 1. 0.333 should be one third of that length.

What to notice if your student does not solve the problem fluently:
Inability to use the divisions on the scale (tenths). This indicates that the student does not understand the relationship between tenths and one. They may also have insufficient experience working with scales.
Locating 0.75 away from the three-quarters position and 0.333 away from the one third position indicates that the student is unaware of common fraction/decimal benchmarks.
Locating 1.95 close to one suggests that the student is not familiar with equally partitioning tenths into hundredths to form more precise locations on a scale.
Supporting activity:
Locating decimals on a scale
- Imagine you have two lengths of rope. One length is 2.8m long and the other is 1.65m long.
You tie the two ropes together and make a new rope that is 3.95m long.
How much length do you lose by tying the ropes together?
Explain how you worked out your answer.
Signs of fluency and understanding:
Connects the context of joining with addition and finds that the total length of the two pieces of rope by 2.8 + 1.65 = 4.45m. Finds the difference between 3.95 and 4.45 by adding on or using subtraction, such as 4.45 – 3.95 = 0.5.
What to notice if your student does not solve the problem fluently:
Recognises that addition is needed to work out the total lengths but incorrectly calculates 2.8 + 1.65 = 3.73. This might indicate that the student treats decimals as whole numbers, and therefore treats the decimal part of the sum as 8 + 65 = 73. They might also calculate 3.95 – 3.73 = 0.22 correctly without realising that the total length must exceed the joined length.
Incorrectly adds 2.8 + 1.65 = 3.73. This might indicate that the student does not understand that ten tenths make one and that this one must be ‘carried’ across the decimal point. The student may see the decimal point as a separation between whole numbers and decimals.
Subtracts 4.45 – 3.95 = 1.5. This indicates that the student subtracts that higher digit from the lower digit without considering whether the digit is in the total length or joined length.
Unable to turn the problem into operations. This may indicate that the student does not associate joining with addition and difference with subtraction in a decimals context. Alternatively, they may be unaware of how to coordinate the multiple steps needed to solve this problem.
Supporting activity:
Adding and subtracting decimals
- Imagine you start a coin trail with ten $2 coins. Each coin measures 2.65 cm across.
How long is the trail?
Show me with your hands how long that is.
Signs of fluency and understanding:
Anticipates the length correctly using multiplication, i.e. 10 x 2.65 = 26.5cm. Shows clearly that 26.5 cm is slightly less than the length of a desk ruler (30cm).
What to notice if your student does not solve the problem fluently:
Inability to turn the problem into an action. This may indicate that the student has yet to transfer their understaiding of multiplication with whole numbers to similar contexts with decimals.
Incorrectly multiplies 10 x 2.65 = 2.650 or 10 x 2.65 = 20.650. This may indicate that the student relies on rules like ‘add a zero’ to multiply by ten.
Repeated addition of 26.5 + 26.5 = 53.0, 53 + 26.5 = 79.5, etc. This indicates that the student has yet to transfer multiplication as repeated addition to decimal situations. If this strategy is used, prompt the student to consider other methods they could use.
Supporting activity:
Multiplying decimals by 10 or 100
Teaching activities