This unit is an introduction to Pythagoras’ Theorem. It includes history, proofs, and practise in the application of the theorem.
- State and explain Pythagoras’ theorem.
- Use Pythagoras’ theorem to find unknown sides of right angled triangles.
This unit looks at using Pythagoras’ Theorem to find unknown sides of right-angled triangles. It also includes three proofs of the Theorem.
The learning opportunities in this unit can be differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- grouping students flexibly to encourage peer learning, scaffolding, extension, and the sharing and questioning of ideas
- apply the gradual release of responsibility to scaffold students towards working independently
- using diagrams and equipment to model concepts and support students' thinking
- allowing the use of calculators to estimate and confirm calculations
- providing frequent opportunities for students to share their thinking and strategies, ask questions, collaborate, and clarify in a range of whole-class, small-group, peer-peer, and teacher-student settings.
The focus of this unit on investigating Pythagoras’ Theorem can be applied to a variety of engaging, real-life contexts, such as the slope of hills, the height of buildings, physical construction problems, navigation, and construction. Session 5 asks students to think of these, however, you could make reference to these contexts throughout the unit.
You can increase the relevance of the learning in this unit by providing ample opportunities for students to create their own problems, create their own representations of a task, and participate in productive learning conversations.
Te reo Māori kupu such as ture (formula, rule), tāroa (hypotenuse), ture a Pythagoras (theorem of Pythagoras), and koki hāngai (right angle) could be introduced in this unit and used throughout other mathematical learning.
Session 1
In this session we look at the history of Pythagoras, introduce the theory, and look at the 3,4,5 triangle using Cuisenaire rods.
- Introduce the subject of Pythagoras, determine what students have has prior knowledge of the man and his work. Below is a brief biography.
Pythagoras of Samos lived from about 569 BC to about 475 BC. He was a Greek philosopher who made important developments in mathematics, astronomy, and the theory of music. He spent most of his life in the Greek colonies in Sicily and southern Italy. He never married, and he had a group of followers who taught other people what he had taught them. The Pythagoreans were known for their pure lives. They wore their hair long, wore only simple clothing, and went barefoot.
Pythagoreans were interested in philosophy, but especially in music and mathematics, two ways they saw as making order out of chaos. Music as noise that has meaning, and mathematics as the whole world reduced to rules.
Pythagoras himself is best known for proving that the Pythagorean Theorem was true. The Sumerians, two thousand years earlier, already knew that it was generally true, and they used it in their measurements, but Pythagoras proved that it would always be true.
- Write up Pythagoras’ Theorem on the board and ask the class to explain what it means using examples.
Pythagoras’ Theorem "For any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.” a2 + b2 = c2 |
This may require some revision of knowledge of geometry. Ensure your students understand what is meant by right-angled triangle (a triangle with 900 as one of its interior angles) and hypotenuse (the longest side of a right-angled triangle, which is always the one opposite the right angle). Also ensure that the class understands what the square of a number is, and what the sum of two numbers means. Explain that the theorem is often stated as a2+b2=c2, where a and b are the short sides and c is the hypotenuse.
- Get the class to help rewrite Pythagoras’ Theorem so it makes sense to them, eg. If you take the length of the longest side of a right-angled triangle and square it, you will always get the same amount as you get if you square the lengths of the other sides and then add them together.
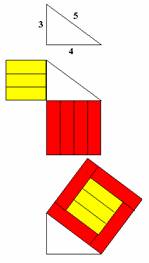
- Support students to demonstrate Pythagoras’ theory for 3, 4, 5 triangle.
- Get each student to draw a triangle with sides 3 cm, 4 cm, and 5 cm.
- Give each student three 3 cm Cuisenaire rods and four 4 cm Cuisenaire rods. Get them to lay out the rods so that they make a square on each of the two shorter sides.
- Instruct students to move the rods to make a square on the hypotenuse. This square uses the same rods to make it as the two smaller squares so it must have the same area.
- Check by using algebra 32+42=9+16
=25
=52
- Discuss whether this proves that the theorem is true (No).
Why or why not? (It only provides an example, we now know it is true for a triangle with sides of 3cm, 4cm, and 5cm).
Can we use this method to prove the theorem is true? (No).
Why or why not? (It will only work effectively with natural numbers, and Pythagoras’ Theorem is true for all right-angled triangles).
- Discuss Pythagorean triples. Challenge students to find another triple where a, b and c are less than 100.
A Pythagorean Triple is a triple of natural numbers (a,b,c) such that a2 + b2 = c2 The following is a list of all Pythagorean Triples where a, b, c are all no larger than 100; (3,4,5), (5,12,13), (6,8,10), (7,24,25), (8,15,17), (9,12,15), (9,40,41), (10,24,26), (11,60,61), (12,16,20), (12,35,37), (13,84,85), (14,48,50), (15,20,25), (15,36,39), (16,30,34), (16,63,65), (18,24,30), (18,80,82), (20,21,29), (20,48,52), (21,28,35), (21,72,75), (24,32,40), (24,45,51), (24,70,74), (25,60,65), (27,36,45), (28,45,53), (28,96,100), (30,40,50), (30,72,78), (32,60,68), (33,44,55), (33,56,65), (35,84,91), (36,48,60), (36,77,85), (39,52,65), (39,80,89), (40,42,58), (40,75,85), (42,56,70), (45,60,75), (48,55,73), (48,64,80), (51,68,85), (54,72,90), (57,76,95), (60,63,87), (60,80,100), (65,72,97). |
Session 2
In this session we explore of proofs of Pythagoras’ Theorem. Depending on your class you might want to use all, some, one or none of these proofs. They could be used in a station approach, as a series of teacher directed explorations, or as a demonstration to the class.
- There have been many proofs of Pythagoras’ Theorem (there are 38 at http://www.cut-the-knot.org/pythagoras/) but one of the clearest and easiest to understand is the one used by Pythagoras himself. The proof can be presented as purely diagrammatic, or the algebra can be included.
- Draw the diagram, label all the sides of triangles and squares as a, b, or c, and colour as shown (or use Copymaster 1).
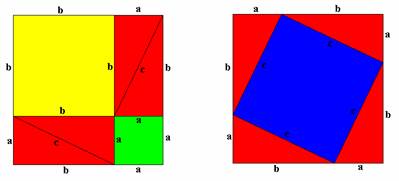
- Ask students to see if they can explain how the diagram illustrates Pythagoras’ Theorem. Discuss suggestions.
- Ask students what the area of the two big squares is (the ones made up of triangles and squares). Support students to understand that hey are both the same size, as demonstrated by (a+b) x (a+b). Does this help prove the theorem?
- If we removed the four red triangles from each diagram, what would be the area of what is left of each big square? For the first square (bxb)+(axa), or a2+b2, and for the second square cxc, or c2. Since the two squares started out the same size and had the same amount taken off them a2+b2 must equal c2.
- For the full algebraic proof, start with the area of each large square, and break it down into the individual shapes.
- The first square: (a+b)2 = a2+b2+4(½ ab). This is worked out by adding the green square, plus the yellow square, plus four red triangles each with area of half base times height (½ ab).
- The second square: (a+b)2 = c2+4(½ ab). This is worked out by adding the blue square, plus four red triangles each with area of half base times height (½ ab).
- Since (a+b)2 = (a+b)2 , we can state a2+b2+4(½ ab) = c2+4(½ ab).
- By subtracting 4(½ ab) from each side we are left with a2+b2 = c2
- For a cut and paste illustration, use Copymaster 2.
- Colour the three squares so that the pieces can be identified.
- Cut out along all the lines and rearrange as shown below.
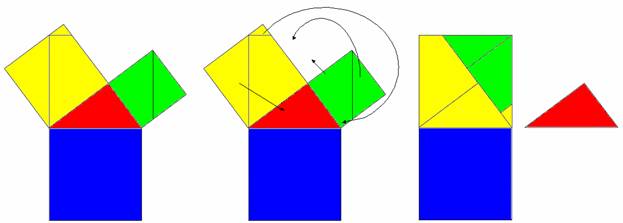
- Clearly the size of the top (green and yellow) square is the same as that of the bottom (blue) square, and since the top square represents the sum of the squares of the two smaller sides and the bottom square represents the square of the hypotenuse the theory is proven.
- Another diagrammatic proof is shown on Copymaster 3.
- Start with the right-angled triangle, and a square drawn on each side.
- Colour the two smaller squares one colour and the larger square a different colour. Pythagoras’ theorem states that these two areas are the same.
- Now colour three triangles the same size as the original one each of the two colours (as illustrated).
- This makes two irregular, but identical, pentagons that clearly have the same area.
- If the two pentagons have the same area, then the two smaller squares must have the same area as the larger one.
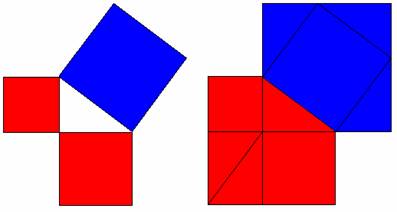
- An interesting class discussion could be based around the question Which of these proofs is the best? (There is no right answer, they all have strengths and weaknesses).
Session 3
This session uses Pythagoras’ Theorem to find the hypotenuse of right-angled triangles.
- Ask the class Now that we know Pythagoras’ Theorem is true, how can we use it?
- Draw a right-angled triangle on the board and label the two shorter sides with the numbers 5 and 8.
- Ask the class for suggestions how they could work out the length of the side that is not labelled.
- Work through the example with the class (an example of this is shown on Copymaster 4).
- Distribute a copy of Copymaster 4 to each student. Those that are confident can work independently, those that are unsure could be guided through another example.
- Early finishers could be challenged to set each other further problems.
Session 4
This session uses Pythagoras’ Theorem to find side lengths other than the hypotenuse.
- Ask the class How can we use Pythagoras’ Theorem to work out a side length other than the hypotenuse?
- Draw a right-angled triangle on the board and label one of the shorter sides 6 and the hypotenuse 9.
- Ask the class for suggestions how they could work out the length of the side that is not labelled.
- Work through the example with the class (see Copymaster 5).
- Distribute a copy of Copymaster 5 to each student. Those that are confident can work independently, those that are unsure could be guided through another example.
- Reinforcement problems involving Pythagoras' theorem, such as those found in textbooks and/or worksheets could be assigned or written on the board.
Session 5
In this concluding session we work on applications of Pythagoras’ Theorem.
- Review with the class Pythagoras’ Theorem. Ask for volunteers to explain their understanding of the Theorem.
- Ask students to suggest a real life examples where it would be useful.
- Work through one or two examples on the board with the class. Ensure that you emphasise the importance of drawing and labelling a diagram, to ensure that you know where the right angle is and which side is the hypotenuse.
- Give out a copy of Copymaster 6 to each student: Those that are confident can work independently, those that are unsure could either be guided through another example or work in pairs.
- Early finishers could be challenged to set each other further problems.
- Leave time at the end of the class to share solutions to the problems.
Dear families and whānau,
Recently we have been investigating the history, proofs, and applications of Pythagoras’ Theorem. Ask your child to share their learning with you.