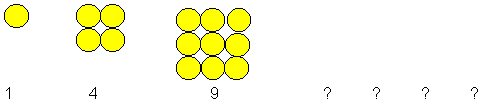
In this unit ākonga look for and describe patterns they see in different types of staircases and other patterns.
- Continue a sequential pattern.
In much of early pattern work, the numbers involved can be compiled in tables like the one below:
| Length of garden | 1 | 2 | 3 | 4 | 5 | 6 |
| Number of paving stones | 8 | 12 | 16 | 20 | 24 | 28 |
Two relationships can be seen:
- The recurrence relation allows us to calculate the next number in the pattern from the previous number. In the example above, the number of paving stones increases by four each time the length of the side garden is increased by one. This pattern can be seen in the second row of the table: 8, 12, 16, 20…
- The functional relationship allows us to calculate any number in the pattern, independent of the previous number. In the example above the number of paving stones is four times the length of the garden, plus four. We can express this relationship as an equation. If P equals the number of paving stones and L equals the length of the garden, then P = 4L + 4.
In practice, recurrence relationships are easier to identify than functional ones.
This unit can be differentiated by varying the scaffolding of the tasks or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- encouraging the use of physical materials (such as blocks, ice-block sticks, pebbles, shells) to create patterns and discover the sequential patterns that follow
- demonstrating to ākonga how to draw patterns and discover the sequential patterns that follow. The use of grid paper could help with these drawings
- grouping together students of mixed mathematical abilities to encourage collaborative learning and sharing of knowledge (tuakana/teina)
- providing opportunities for ākonga to create their own patterns throughout the unit. These could be extended by a certain number of iterations and a generalisation could be made. Ākonga could ask others to continue their pattern to check whether it is valid
- adjusting the expectations for solutions - some ākonga may extend the pattern by one or two iterations, while others may describe a generalisation.
The materials used in this unit can be adapted to recognise diversity and ākonga interests to encourage engagement. Instead of creating patterns with classroom blocks or cubes, ākonga could be encouraged to make the patterns using environmental materials such as pebbles, shells, or daisies from the school lawn. Be sure to discuss patterns that your ākonga know about from their personal experience, for example, staircases at home or at the local library, ladders in the kura playground and patterns they have seen at marae or in the community garden.
Te reo Māori vocabulary terms such as tauira (pattern) and the phrase, e hia? (how many) could be introduced in this unit and used throughout other mathematical learning.
- Multi-link cubes
- Staircase problems
- Graph paper
- Coloured pencils
- Other items that could be used for pattern creating (for example, ice-block sticks, pebbles, shells, daisies from the school lawn)
- Copymaster of problems
Getting Started
Today we explore up-and-down staircases to find the pattern in the number of blocks they are made from.
Begin the session by telling ākonga about up-and-down staircases. This type of staircase can be likened to traditional lattice poutama which can be found on tukutuku panels in many marae.

One block is needed to make a 1-step up-and-down staircase. It takes one step to get up and one step to get down. 
This is called a 2-step staircase, as it takes two steps to go up and two steps to go down.
- Together count the steps so that ākonga understand why it is called a 2-step staircase. If possible, observe staircases in your school, and count how many steps it has.
How many blocks are in the staircase?
How many blocks do you think would be in a 3-step up-and-down staircase?
How could you work it out? - Give ākonga time to work out the number of blocks. Ākonga could use blocks, draw or think about the result. Share the ways that they used to work it out.
- Ask ākonga to guess how many cubes they think would be needed to make a 5-step staircase. Get them to build a 5-step staircase. Check their guesses.
Get ākonga to build more staircases. As they do, ask them about any patterns they see.
Some may recognise the horizontal layers as being the sequence of odd numbers. Some may see the vertical stacks.
Some may see that square numbers of blocks are always involved. This can be checked by rearranging the blocks to make square numbers (see the diagram below). This is an important discovery. Let them make it. This may require some careful scaffolding on your part. Ask ākonga to make several squares and look for patterns. The first square is 1 block, then the next square is 1 + 3 followed by 4 + 5. The square term is a number raised to the second power (n2 e.g., 2 x 2 = 4). Using blocks to build some squares and then asking ākonga to draw three more builds a good understanding of square numbers.

.gif)
- Some ākonga may wish to continue to find numbers that make larger up-and-down staircases. To keep track of the number of blocks/cubes in each staircase it might be useful to draw the staircases on graph paper. Other ākonga will prefer to use cubes. Demonstrate and show ākonga how they can record their results in a table.
- There could also be an opportunity for some ākonga to create their own staircase patterns to help challenge their thinking at this early stage of the unit.
Exploring
Over the next 2-3 days, ākonga work in pairs or individually to solve the following problems (Copymaster of problems). A tuakana/teina model could work well here. Show ākonga how to use grid paper to draw the patterns and continue them. They could also use materials. As ākonga complete the problems, ask them about any patterns they see and encourage ākonga to record these observations with the patterns on the graph paper or by building the patterns with materials. Ākonga can also record their patterns using a table. The teacher will need to demonstrate how to do this and potentially provide blank tables for ākonga to use. For example:
| Pattern Number | 1 | 2 | 3 | 4 | |
| Number of Blocks |
Problem 1: Straight up the stairs
How many blocks are in this 4-step-up staircase?
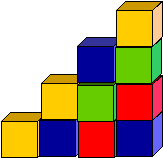
How many blocks would there be in a 5-step-up staircase?
How many blocks would there be in a 6-step-up staircase?
How many blocks in a 10-step-up staircase?
How many more blocks will an 11-step-up staircase need?
What is the largest up staircase that you can tell us about?
Note: the numbers of blocks in this pattern are the triangular numbers, see Algebra Information.
Problem 2: Climbing ladders
How many pieces of wood have we used in this 1-rung ladder?
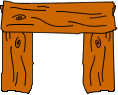
How many pieces of wood have we used in this 2-rung ladder?
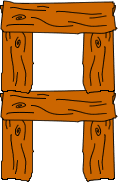
How many pieces of wood would there be in a 4-rung ladder?
How many pieces of wood would there be in a 6-rung ladder?
What is the largest ladder that you can tell us about?
How many pieces of wood will you need to add to a 7-rung ladder to get an 8-rung ladder?
Note: the number of pieces of wood is three times the number of rungs.
Ice-block sticks could be used to create ladders.
Problem 3: Small steps
Watch out! You need to take small steps to walk up and down these little stairs.
 | 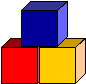 | 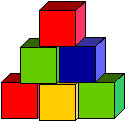 |
| 1-step | 2-step | 3-step |
How many blocks are in the 4-step staircase?
How many blocks are in the 6-step staircase?
What is the largest staircase that you could tell us about?
Does this remind you of something you have done before?
Note: the count here is the same as that in Problem 1.
Problem 4: Star patterns
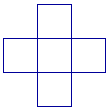 | 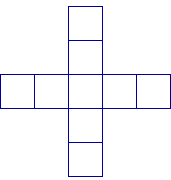 | |
| This is a 1-star | This is a 2-star | This is a 3-star |
How many blocks are in a 4-star?
How many blocks are in a 5-star?
What do you notice about the stars?
How many blocks do you need to add to a 7-star to make an 8-star?
What is the largest star that you could tell us about?
Note: the pattern here is 1, 5, 9, 13, … At each stage you add on 4 blocks. To make a 100-star you need to have 99 lots of 4 plus one block for the centre.
Problem 5: L-shapes
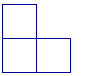 |  | |
| This is a 1-L | This is a 2-L | This is a 3-L |
How many blocks are in a 4-L?
How many blocks are in a 5-L?
What do you notice about the pattern in the L’s?
What is the largest L that you could tell us about?
Note: to make a 100-L you need 100 + 100 – 1 = 199 blocks.
Reflecting
In this session we share our findings and solutions to the problems of the previous days. We listen and look carefully as the patterns are explained. We then make some block patterns of our own which we give to our classmates to continue.
- Begin the session by asking ākonga to attach and display their solutions to the problems on a display wall or table. These solutions could be constructions out of materials, drawings on grid paper, tables or oral/written explanations. Give ākonga time to look at the solutions of other ākonga. Pairs of ākonga could share with other pairs of students. Encourage ākonga to share their solutions with the class.
- Give pairs of ākonga a supply of blocks (or other objects) and grid paper and ask them to invent their own pattern. A tuakana=teina model could work well here. Ask them to record the first three elements in the pattern on a piece of grid paper. They could also make a table to explain their pattern.
- Ask ākonga to swap patterns with another pair. Work together to discover the pattern and then continue it.
- Repeat with another pair’s pattern.
- Leave the patterns on a table for all ākonga to solve in their own time.
Dear parents and whānau,
In maths this week we have explored different block patterns.
Discuss the pattern with your child and see if they can continue the pattern. You may want to find some objects your child could make this pattern out of, for example, pebbles or coins.