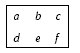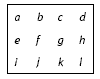Pyramid Parts

This activity encourages students to think systematically about particular arithmetic structures or equations.
In question 1, suggest to students who have difficulty seeing how the top pyramid number can be found that they first use only the numbers in the base of the pyramid.

Some students may need to explore several 3-level pyramids in this way before they can suggest a rule for finding the top pyramid number, given the three base numbers. Note that the rule will be easier to discover if they ensure that the three base numbers are all different. Encourage the students to check if their rule works for large whole numbers, decimal numbers, and numbers in which one or more digits are zero.
This could be a good opportunity to introduce the use of symbols (or variables) that stand for any number and to show how they can help us understand what is going on in the general case. For example, if the base numbers are we obtain the 3-level pyramid:

Here, the symbols stand for any numbers and are used in exactly the same way as the algebraic symbols a, b, c, ... x, y, z are frequently used.
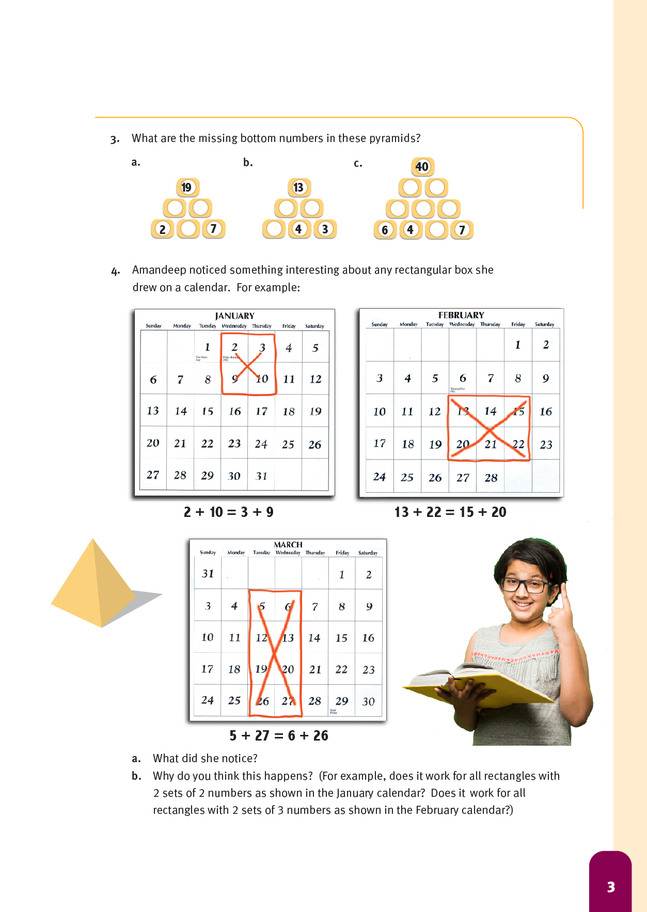
The first two examples in question 2 give the students an opportunity to consolidate their thinking on how the rule works for a 3-level pyramid and then to use this thinking as the basis for a sensible prediction for how to get the top number for a 4-level pyramid (questions iii and iv). The students could check their predictions by using only the base numbers to form 4-level pyramids. For example:

In this pyramid, the top pyramid number is 1 + (3 x 2) + (3 x 3) + 4, which is 1 + 6 + 9 + 4 = 20. Once again, symbols could be used to help confirm the rule the students have discovered. Some students may want to see if they can predict what will happen for a 5-level pyramid, a 6-level pyramid, and so on. All predictions
need to be checked carefully.
In question 3, the top pyramid number is the starting point for finding the missing number in the base of the pyramid. The students need to reverse their thinking (although some may find the solution through guessing and checking for the missing base number). In question 3a, for example, the rule for the 3-level pyramid tells
us that 2 x the missing number + 2 + 7 = 19. This means that the missing base number is half of 10 (the answer to 19 – 2 – 7). In question 3b, the missing base number is 13 – 3 – (2 x 4) = 2. In question 3c, the missing base number is one-third of the answer to 40 – 6 – 7 – (3 x 4). So the missing base number is one-third of 15, which is 5. Students who are able to reverse their thinking in this way show that they
understand the rule linking the top pyramid number with the numbers in the base of the pyramid. Encourage the students to explain their thinking.
In question 4, the students see if they can spot the relationships between corner numbers in rectangular arrays of different sizes, located on calendars for different months. Encourage the students to talk with others about what they see before they try to write anything. If you explain the links, you will limit the exciting moments when students “see” the links themselves. Searching for mathematical similarities as well as
differences is the process that enables students to make mathematical generalisations

Answers to activity

1. a. Yes.
b. The middle number is added twice, and each outside number is added once
(2 x 5 + 6 + 4 = 20 or 4 + 2 x 5 + 6 = 20).
2. a. i. 19
ii. 27
iii. 24
iv. 67
b. A possible explanation is: for 3 tiers, add the outside numbers to 2 times the inside number. For 4 tiers, add the outside numbers to 3 times the sum of the inside two numbers.
3. a. 5
b. 2
c. 5
4. a. She noticed that the numbers in opposite corners of a calendar rectangle add up to the same total.

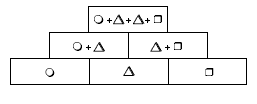
b. In a calendar, the numbers across a row are in numerical order (1, 2, 3, 4, …) and the difference between each number in a column is 7 (2, 9; 3, 10; and so on). This means that for a 2 by 2 rectangle, a is 1 less than b but d is 1 more than
c:

This ensures that a + d = b + c.
For a 2 by 3 rectangle, a is 2 less than c but f is 2 more than d:

For a 3 by 4 rectangle, a is 3 less than d but l is 3 more than i:

So it does work for all calendar rectangles with 2 sets of 2 numbers or 2 sets of 3 numbers.