This unit introduces the fact that fractions come from equi-partitioning of one whole. Therefore, the size of a given length can only be determined with reference to the size of one whole. Usually the one must be defined in context.
- Name the fraction for a given Cuisenaire rod with reference to one (whole).
- Give the relationship between one Cuisenaire Rod and another, especially when one rod is a fraction of the other.
- Add and subtract fractions by expressing fractions as equivalents with the same denominator.
- Order fractions using methods such as benchmarking to zero, one half or one, identifying equivalent fractions and comparing numerators and denominators.
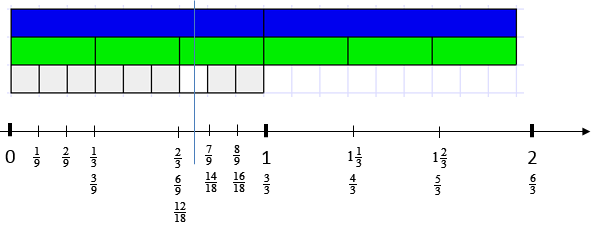
‘Fractions as measures’ is arguably the most important of the five sub-constructs of rational number (Kieren, 1994) since it represents fractions as numbers, and is the basis of the number line. Fractions are needed when ones (wholes) are inadequate for a given purpose (e.g. division). In measurement, lengths are defined by referring to some unit that is named as one. When the size of another length cannot be accurately measured by a whole number of ones then fractions are needed.
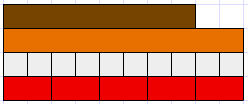
For example, consider the relationship between the brown and orange Cuisenaire rods. If the orange rod is defined as one (an arbitrary decision) then what number do we assign to the brown rod?
Some equal partitioning of the one is needed to create unit fractions with one as the numerator. For the size of the brown rod to be named accurately those unit fractions need to fit into it exactly. We could choose to divide the orange rod into tenths (white rods) or fifths (red rods), either would work. By aligning the unit fractions we can see that the brown rod is eight tenths, or four fifths, of the orange rod.
Note that eight tenths and four fifths are equivalent fractions and that equality can be written as 8/10 = 4/5. These fractions are different names for the same quantity and share the same point on a number line. This idea, that any given point on the number line has an infinite number of fraction names, is a significant conceptual change compared to understanding of whole numbers. Some names are more privileged than others by our conventions. In the case of four fifths, naming it as eight tenths aligns to its decimal (0.8), and naming it as eighty hundredths aligns to its percentage (80/100 = 80%).
‘Fractions as operators’ is another of Kieren’s sub-constructs and applies to situations in which a fraction acts on another amount. Some examples are:
- that amount might be a whole number, e.g. three quarters of 48
- a decimal or percentage, e.g. one half of 10% is 5%
- or another fraction, e.g. two thirds of three quarters.
A confusion students sometimes have is when fractions should be treated as numbers and when they should be treated as operators. A particular case us when creating numbers lines, e.g. they often place 1/2 where 2 1/2 belongs on a zero to five number line.
Specific Teaching Points
Understanding that fractions are always named with reference to a one (whole) requires flexible thinking. Lamon (2007) described re-unitising and norming as two essential capabilities if students are to master fractions. By re-unitising she meant that students could flexibly define a given quantity in multiple ways by changing the units they attended to. "Norming" is the process of operating with new units. In this unit Cuisenaire rods are used to develop students’ skills in changing units and thinking with those units.
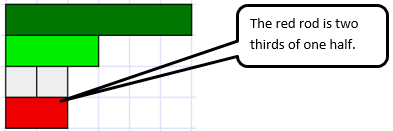
Multiplication of fractions involves adaptation of multiplication with whole numbers. Connecting 'a x b' as ‘a sets of b’ (or vice versa) with a/b x c/d as ‘a b-ths of c/d’ requires students to firstly create a referent whole. That whole might be continuous, like a region or volume, or discrete like a set. Expressing both fractions in a multiplication and the answer requires thinking in different units. Consider two thirds of one half (2/3 x 1/2) as modelled with Cuisenaire rods.
Let the dark green rod be one, then the light green rod is one half.
So which rod is two thirds of one half? A white rod is one third of light green so the red rod must be two thirds. Notice how we are describing the red rod with reference to the light green rod.
But what do we call the red rod? To name it we need to return to the original one; the dark green rod. The white rod is one sixth so the red rod is two sixths or one third of the original one. So the answer to the multiplication is 2/3 x 1/2 = 2/6 or 1/3.
Reunitising and norming are important when fractions are placed in order of size (magnitude). This is especially true given any fraction has an infinite number of names. Imagine we use the orange rod as one this time and find two fifths. Since five red rods measure one whole (orange rod) then two red rods measure two fifths:
But, what other names does two fifths have? If the red rods were split in half they would be the length of white rods and be called tenths since ten of them would form one. The crimson rod is equal to four white rods which is a way to show that 2/5 = 4/10.
If the red rods were split into three equal parts the new rods would be called fifteenths since 15 of them would form one. The crimson rod would be equal to six of these rods which is a way to show 2/5 = 6/15. The process of splitting the unit fraction, fifths in this case, into equal smaller unit fractions, is infinite. This means that the point on the number line where two fifths exist has an infinite set of number names.
This unit is set for students to learn, and practice, outcomes at Level 4 of mathematics in the New Zealand Curriculum. Differentiation involves simplifying or adding more challenge to the tasks in the following ways:
- varying the level of abstraction, that is the extent to which operations are carried out mentally rather than through actions on materials. Cuisenaire rods are the manipulatives used in the unit. Encourage abstraction by asking predictive questions, e.g. “What fraction do you think will be the difference between x and y?”
- making clear links between the numerator as a counter, and the denominator as the number of parts in a whole. Link fraction symbols with the Cuisenaire rod models students create
- controlling the fractions used in the problems so they can be physically modelled before extending the range of fractions to numbers outside what can be easily modelled. Halving related fractions, i.e. quarters, eighths, sixteenths, etc., tends to be easier than fractions with odd denominators, i.e. thirds, fifths, sevenths, etc.
- managing the reading and recording demands of tasks, particularly by allowing students to record their thinking in their own way before supporting them toward conventional symbolic recording
- encouraging students to work collaboratively in partnerships, and to share and justify their ideas (a tuakana/teina relationship could be used)
- regularly sharing ideas with the whole class.
The context for this unit is not real life. However, a story shell such as construction beams, waka lengths, or steps, might be used if there is potential to motivate students. Most students will enjoy the opportunity to work with Cuisenaire rods.
Te reo Māori vocabulary terms such as hautanga (fraction), hautau ōrite (equivalent fraction), tauira (patterns), tauraro (denominator) and taurunga (numerator) could be introduced in this unit and used throughout other mathematical learning.
- 1 cm squared paper
- Cuisenaire rods or access to the online Cuisenaire rods tool
- Copymaster 1
- PowerPoint 1
Prior Experience
Students may have limited experience with using Cuisenaire rods. Their lack of familiarity with the rods is a significant advantage as they will need to imagine splitting the referent one to solve problems. When introducing the Cuisenaire rods, ask students to think about what they could be used to represent in mathematics. Value the contributions of all students.
Session One
Consider providing a story context to frame the learning in this session (e.g. construction beams, waka lengths, length of a running track). Links will be engaging when they reflect the cultural diversity and/or learning interests of your students. This context could stay consistent in every session. Alternatively, you could introduce each session with a new relevant context to enhance students’ understanding of the mathematical concepts covered in these lessons, to real-world situations.
- Use Cuisenaire rods or the online tool to introduce equivalent fractions in the following way. Use a digital display, whiteboard, or large sheet of paper to record students' ideas.
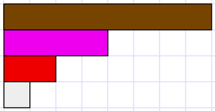
What is the size of the crimson rod compared to the brown rod? How do you know?
The relationship between the crimson and brown rods can be expressed in two ways:- “The crimson rod is one half of the brown rod.”
- “The brown rod is two times the length of the crimson rod.”
- Ask: So if the brown rod was one then the crimson rod would represent one half. What fraction would the red rod and white rod represent? How do you know this is true?
Encourage the students to express the relationships in various ways, such as:- “The red rod is one quarter of the brown rod because four of it fit into one (brown rod).”
- “The brown rod is four times longer than the red rod.”
- Ask: How many quarters and how many eighths are the same length as one half (crimson rod)?
How might we record these relationships mathematically?
Hopefully students will suggest recording an equality like this: 1/2 = 2/4 = 4/8. - Ask: What patterns do you see?
Students should notice the doubling of both numerators and denominators. “Why does this happen?”
It is important to reinforce the idea that the numerator is a count, so the doubling of numerators indicates that there are twice as many parts in the same space. - Ask: But why do the denominators double? Does that mean that the parts get twice as big?
Look for the students to notice that the denominators double because the parts halve in size - meaning twice as many quarters as halves fit into one, and twice as many eighths as quarters fit into one. - Use slide one from the PowerPoint for this unit.
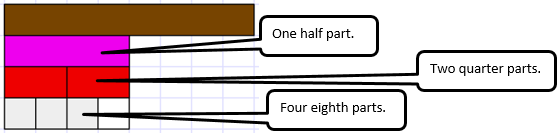
Ask: Imagine we had these new rods, grey and pale blue. What could you say about these new rods in relation to one (the brown rod)? How would you write the relationships mathematically? How are these fractions related to one half?
Look for students to establish grey as one sixteenth either by halving one eighth or realising that sixteen of the parts fit into one. Discuss the pale blue rod and its relation to the brown and grey rods. Equivalent fractions for one half can be found. Record these fractions as equalities:
1/2 = 8/16 and 1/2 = 3/6 - Ask: What patterns can you see? Explain why the patterns occur.
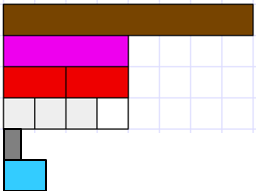
Look for students to use numerator as a count and denominator as the number of equal parts that fit into one. - Introduce Investigation One using slide two of the PowerPoint. Provide sets of Cuisenaire rods or access to the online tool. Let the students work in small teams (mahi tahi relationship). It may be necessary for you to work with a small group of students. Look for the following: Do the students refer back to the brown rod as the one? Do they look for a unit fraction to support them to name the green and orange rods?
- Can they record the relationships they find as equalities?, e.g. 3/4 = 6/8.
- Can they conjecture equivalent fractions that they do not have rods for?, e.g. 5/8 = 10/16
- All of these points can be raised in discussion as a whole class. Continue to ask questions about the meaning of the numerators and denominators in equivalent fractions. For example, us the orange rod as one and find how many tenths equal one half and equal three fifths.
- Finish the session with a reflection question: “Two children are talking (see slide three of the PowerPoint). Millie and Jana have different ideas about two thirds. Who is right? Explain why they are right.”
- Let the students write an answer individually. You might use your students’ writing as prior assessment and revisit the idea of an infinite number of equivalent fractions sometime later.
Session Two
- Revise the key points about equivalent fractions from the previous session using the dark blue rod as one.
Ask questions like:
If the dark blue rod is one what do we call the light green and white rods? Justify your answers.
What statements can you make about the relative size of the rods?
Can you create an equivalent fraction to two thirds using rods in the picture (2/3 = 6/9)? How might we record this equality? - Show the students slide four of the PowerPoint for this unit. Create a fictitious fawn coloured rod by joining two dark green rods. On the online tool you can set the rod length to 12 to make the rod. The students might notice that the light green rod is one quarter since it maps into one four times and that the crimson rod is 1/3 and fits the fawn rod three times. If they do not, scaffold this understanding. Use the physical materials to demonstrate the relationship. At this point you might construct this diagram using the online tool with the fawn rod being made up of length 12 (two dark green rods).
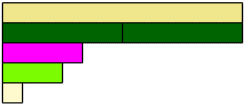
- Invite students to describe the total length of the crimson and light green rods combined. Look for ideas like:
The total is more than one half because two quarters is one half and one third is longer than one quarter.
- Ask: What rod could we use to measure all three rods exactly, light green (one quarter), crimson (one third) and fawn (one)?
Different rods might be tried but the white rod is the only unit that measures all three. - Ask: What fraction of one is the white rod? (one twelfth because 12 of those rods fit into one)
How many twelfths are the crimson rod (one third) and the light green rod (one quarter)?
How could we record these equalities? (1/3 = 4/12 and 1/4 = 3/12)
So what is the total length of one third plus one quarter? (seven twelfths)
How might we record this sum mathematically?
Where do the seven and the twelve in the answer come from?
Students might notice that if the sum is written as 1/3 + 1/4 = 4/12 + 3/12 = 7/12 then the origin of the seven and twelve are clear.
Why are twelve and twelve not added? The units are twelfths so we get “Four twelfths plus three twelfths equals seven twelfths.” - Provide the students with a set of Cuisenaire rods and Copymaster 1 for each small group. Let them solve the problems collaboratively as you roam. Look for the following:
- Can the students name each fraction with reference to the designated one rod?
- Do they look for equivalent fractions where they are needed?
- Do they record the addition of each pair of fractions correctly?
- Look especially for how they deal with non-unit fractions, like three quarters.
- After a suitable period, bring the class together to discuss their solutions. Bring out the points above. Look for students to justify their renaming of fractions in equivalent form and how they calculated their answers. For example, in question 4 the sum can be written: 1/2 + 3/7 = 7/14 + 6/14 = 13/14.
- Pose a problem for individuals to solve and record their thinking (see slide six of the PowerPoint for this unit). You may like to use this to assess who among your students understands addition of fractions and who needs further support.
Session Three
In this session the purpose is to find the difference between two fractions. Difference is the often neglected context for subtraction though problems can also be solved by adding on.
- Pose this problem:
Lelani got two thirds of a whole Cuisenaire rod and Sala got one half of the same sized Cuisenaire rod. Who got the most and how much more of one rod did they get? - Ask the students which Cuisenaire rod they could use to solve the problem. Note that it must be possible to make one half of the rod and two thirds of the rod. You may need to try various rods before dark green is settled on. The difference is the length missing to make the smaller fraction as big as the larger.
Students might recognise that the difference is one sixth of the one (dark green). Scaffold this understanding if it is not demonstrated in discussion. Use physical materials to demonstrate the relationship. Ask how this problem might be recorded mathematically. Both addition and subtraction might be used:
1/2 + 1/6 = 2/3 or 2/3 - 1/2 = 1/6. - Ask: So why is the answer one sixth when neither of the fractions have sixths?
Look for students to recognise from previous sessions that both one half and two thirds can be expressed as sixths. So an extra step in the subtraction equation gives:
2/3 - 1/2 = 4/6 - 3/6 = 1/6
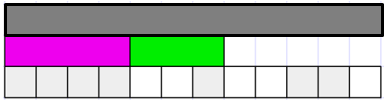
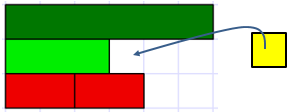
From this recording, students might realise that recording difference as subtraction is a little tidier and certainly more conventional than adding on. - Build this diagram:
- Ask the students to discuss in pairs what fraction difference problems might be made up using this picture. Remind them to think flexibly about which rod is one, assuming the orange rod is one is not the only possibility (dark green and yellow can also be named as one).
- Record a few possible problems such as:
- If the dark green rod is one, what fractions are represented by the orange and yellow rods?
- What is the difference between those two fractions? In this case the orange rod represents one and two thirds or five thirds of the dark green rod. The yellow rod represents five sixths of the dark green rod.
- So the difference between these two rods represents 5/3 - 5/6. Using white rods to represent sixths then five thirds (orange rod) can be renamed as ten sixths.
Visually we can see that the difference between the two rods is five sixths which matches the calculation: 5/3 - 5/6 = 10/6 - 5/6 = 5/6.
- Let the students attempt Investigation Three (slide five of the PowerPoint) in small groups. They will need a set of rods or access to the online tool, and a means to record their problems, e.g. squared paper. Encourage the students to create differences that they have not seen in the examples you have provided and to use non-unit fractions like two thirds or three quarters. Look for students to use two main approaches, start with the rods they are finding the difference for, or start with a one rod (whole) and experiment with different fractions of that one. Key things to look for are:
- Approach One
Do the students start with two lengths, made with single rods (unit fractions) or collections of rods (non-unit fractions)?
Are they able to create a one (whole rod) that works for both rods?
Do they recognise what unit can be the common denominator and rename each fraction?
Can they find the difference and record the result as a subtraction equation? - Approach Two
Do they choose or create a one rod that has a length with many factors?, e.g. 18cm is useful but 19cm is not so useful.
Do they map other rods onto the one rod to create unit and non-unit fractions?
Can they name the fractions they create?
Do they use smaller rods to convert each fraction to equivalent forms before finding the difference?
Can they find the difference and record the result as a subtraction equation?
- Approach One
- As you roam choose examples of problems students create. Ask students to record their problems. Also expect them to annotate the document to explain how the model shows a particular difference problem, including words and equations.
- At the end of the lesson ask several groups to present their problems for others in the class to solve. Record the three examples vertically. You should have equations that look like this:
1/2 - 3/8 = 4/8 - 3/8 = 1/8 - Ask the students: Imagine someone new came to class who has not solved problems like this before. What would you tell them about how to solve any fraction difference problem?
- Give students time to record instructions/ideas they would give to the new class member. Look at these work samples to assess whether individual students have generalised how to solve difference problems.
Session Four
The aim of this session is to develop students’ mental number line for fractions and develop their capacity to use the number line to find differences between fractions. Inclusion of fractions with whole numbers on the number line requires some significant adjustments. These adjustments include:
- Locating fractions on a number line requires a fixed length of one
- A point on the number line can have an infinite number of names called equivalent fractions, e.g. 2/3, 4/6, 6/9, … all ‘live’ at the same point
- Between any two fractions are an infinite number of other fractions
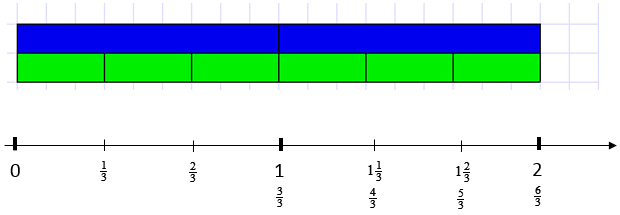
- Begin by building up a number line for thirds in this way. You may want to use the online tool on an interactive whiteboard so the image can be written over.
If the blue rod is one (mark zero and one on the number line) where would one third be? You could scaffold this further by marking zero and one on a number line below the Cuisenaire rod. - Students may recognise that the light green rod is one third of the blue rod. Ask them what fractions could be marked on the number line using one third. Look for them to explain that thirds can be ‘iterated’ (place end on end) to form non-unit fractions, like two thirds. Make sure you push the iteration past one and include the fraction and mixed number ways to represent the amount (see below). Also encourage renaming in equivalent form where this is sensible, e.g. 3/3 = 1, 6/3 = 2.
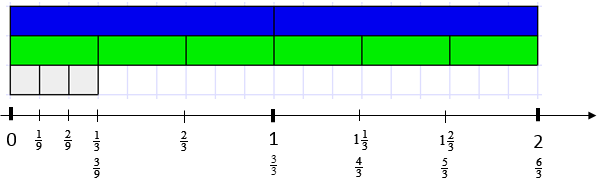
- Look at the space between zero and one third. Ask, “Are there any fractions that belong in this space?” Students may recognise from previous work that white rods are one ninth of a blue rod. One ninth, and two ninths, will work. Ask students to estimate the exact location of these fractions and check using white rods. Note that three ninths equals one third so can be added to the existing number line in the same position as one third.
- Ask: So what unit fractions would exist between zero and one third? (any unit fraction with a denominator greater than three since it will be less than one third, e.g. 1/6, 1/8).
Note that there is no rod in the set that is one quarter, one fifth, one sixth, etc. of the blue rod. However, imaging how long the rods for these fractions would be is a useful activity in itself. - Look at other spaces on the thirds number line and ask students to name fractions they think exist in that space. For example, between two thirds and one are seven ninths, and eight ninths. Imagine cutting each white rod in half.
What fraction will this new rod represent? (eighteenths).
Can we express some of these fractions as eighteenths?
Can we find locations for numbers of eighteenths that are not showing yet?
Students might realise that having eighteenths allows them to find fractions exactly in the middle between numbers of ninths, e.g. 13/18 is exactly half way between 2/3 (6/9) and 7/9. - Show the students slide six (Investigation Four) of the PowerPoint. Choose two of the rods as representing the fractions to compare, for example dark green and orange.
If I say dark green represents one half, how big is one?
Students should recognise that the fawn rod (12 cm) equals one (whole).
If dark green represents one half, what fraction is represented by the blue rod?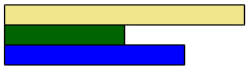
Students should realise that the blue rod represents three quarters, if the fawn rod equals one.
What fraction is the difference between one half and three quarters?
The light green rod is the difference and that rod represents one quarter. Record the difference using a subtraction equation.
3/4 - 1/2 = 1/4 - Allow students plenty of time to investigate differences using the four rods on Slide 6. If possible use the online tool to support their thinking. Students might screengrab the model of their fractions. For example the yellow rod might represent one quarter.
The dark green rod is six twentieths or three tenths of the one rod.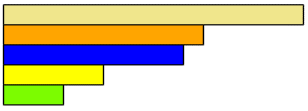
The difference between three tenths and one quarter is one twentieth (the white rod).
The equation for the difference is 3/10 - 1/4 = 1/20 or 6/20 - 5/20 = 1/20
Lesson Five
- Show the students Investigation Five (Slide 7). You may want to give them paper copies as well.
What information is present?
What helpful information is missing?
You need to see this problem as a riddle. There is enough information to put any fraction you want on the number line.
What does to scale mean? - Let the students investigate the task in small groups. They will need a set of Cuisenaire rods or access to the online tool, and squared paper to record on. The squared paper will help them to maintain scale.
Look for the following:- Do the students realise that the white rod is one fifteenth by finding the difference between two thirds and three fifths?
- Do they realise that fifteenths can be iterated to the left and right to find the location of zero and one?
- Having established one as a length of 15cm, can they find the location of other fractions, such as yellow as one third and light green as one fifth?
- After a suitable period of investigation, bring the students together to share some solutions. Highlight the correct use of scale using the one rod as a reference unit. Recognise if some students have included fractions greater than one, e.g. 4/3 = 20/15. The work sample might be used as assessment data but you may like to give students the investigations on slides eight and nine of the PowerPoint as individual assessment. Ask students to record how they worked out the location of the numbers. There are many different ways but all strategies require students to show understanding of equivalence.
Dear parents and caregivers,
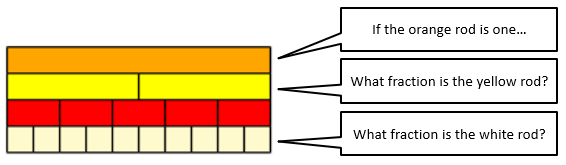
This week your son or daughter will be learning about fractions, for example, three quarters and two thirds. We will be using some materials called Cuisenaire rods which are lengths of plastic or wood. They look like this:
Your son or daughter should be able to name fractions of a given rod. For example, they might say that the light green rod is three fifths of the yellow rod.
There is an online tool that lets you play with Cuisenaire rods on this page: