Introduction
What we want to discuss in this seminar is some of the underlying ideas of problem solving. As we think this is best done by looking at an example, we will consider the following problem:
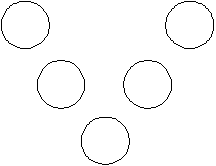
Can you put the numbers 1, 2, 3, 4, and 5, one per circle, so that the numbers on the left hand side of the V add up to the same as the numbers on the right hand side of the V?
With the help of this problem we hope to
- see how mathematicians operate by working through a completely novel situation and trying to develop a mathematical theory around it; and
- show what generalisations, extensions, conjectures, theorems, and proofs are;
The material for this staff meeting is based on the Level 5 Problem Solving unit V-numbers. You might like to have a quick look at it before you run this seminar.
We have also included some copymasters (PDF, 52KB) that may be helpful for this seminar.
Having A Go
First pose the problem and give the staff a chance to solve it. As they come up with answers, ask them if there is another answer and if the answers they have found are different from the previous ones.
As the result of this experimenting, you should come up with essentially three answers. These have, respectively, 1, 3 and 5 at the point of the V.
It is not possible to put 2 and 4 at the point of the V. Why not?
What Have You Done?
Having reached this point the problem seems to be more or less solved. Point out that so far the staff has covered the following sections of problem solving:
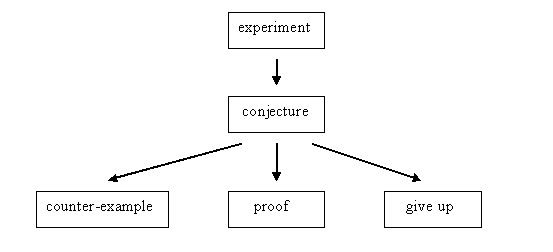
Experimenting is the first thing that mathematicians do when they see a problem. They just play around and hope for inspiration. This is the process that your staff went through at the beginning when they first saw the problem. They had to decide what methods might work and try something to see where it led.
The experimental stage ended about where there was general agreement that there were only three answers. At that point you we are pretty convinced that there were only three answers. This was the conjecture stage. You guessed that there were only three answers.
Round about then, we hope that you pushed them to show you that 2 and 4 didn’t work on the point of the V. So having covered all possibilities for numbers at the point of the V, you had come up with a proof (you had justified) of your conjecture.
But not all conjectures are true. Some are false and so there are things that don’t fit in with the conjecture. Such a misfit is called a counter-example. For instance, suppose we had conjectured that there were just two answers. When we had found the third answer that would have been a counter-example to the conjecture as it would not have fitted in to the conjecture.
Note that there is a box that we haven’t talked about so far. This is the give up stage. Not all mathematicians can solve all of the problems that they attempt. There are a lot of famous problems, such as Fermat’s Last Theorem, that have taken over a hundred years to solve. Even the best mathematical minds have had to give up on that one. So it’s no disgrace to have to give up.
As we said earlier, these are stages that all mathematicians go through when they are trying to solve a problem or develop a theory. But there are more.
The Next Step
Having solved the problem mathematicians don’t just give up and move on to the next one. They actively seek to make things more difficult. Let’s see this by looking back at our V problem. Before we go any further, it’s useful to have a definition that will enable us to avoid unnecessary repetition. So we define a V-set to be a set of five distinct numbers that can be put into the five circles that form a V, so that the sum of the numbers on the left hand side of the V is the same as sum on the right hand side.
Now look at what you've done. You’ve been able to show A and B and you knew C right from the start.
A. {1, 2, 3, 4, 5} is a V-set.
B. {1, 2, 3, 4, 5} is a V-set in three ways.
C. There are two circles on each of the ‘arms’ of the V.
So what can you do next? There are various ways that you can play around with the problem to make it ‘bigger’. Here are some possible ideas. You might like to suggest one or two to get your staff thinking and then sit back to see what they come up with.
A1: What other sets are V-sets?
A2: Are there any sets that are not V-sets?
A3: Can we find all V-sets?
B1: What sets are V-sets in three ways?
B2: What sets are V-sets in just two ways?
B3: What sets are V-sets in just one way?
C1: What if there are three circles on each ‘arm’?
C2: What if there are two circles on one ‘arm’ and three circles on the other?
C3: Put as many circles on each side as you like.
Have a crack at whichever of these ideas takes people’s fancy. After a while get them to summarise what they have done.
More Meta-mathematics
What we have just gone through is the generalisation-extension stage of the research mathematician. This extends the diagram we had above so that it looks like the one below.
So what do these two words mean? A generalisation of a problem is a new problem which contains the first problem as a sub-problem. This is so that when we solve the generalisation we have also solved the original problem. A1 above is a generalisation of the original problem. If we can find a rule for obtaining all V-sets, then we can apply that rule to the set {1, 2, 3, 4, 5} and know immediately that this special set is a V-set (which was what the original problem asked). For instance if we are able to show that every set of five consecutive numbers is a V-set, then we know straight away that the set {1, 2, 3, 4, 5} is a V-set.
An extension is a problem that is based on the original problem, is like the original problem, but does not contain the original as a special case. C1 and C2 are both extensions of the problem that we started with. They are clearly based on the same idea. However, if we solved either one of these we would not immediately have a solution to the problem that began this meeting.
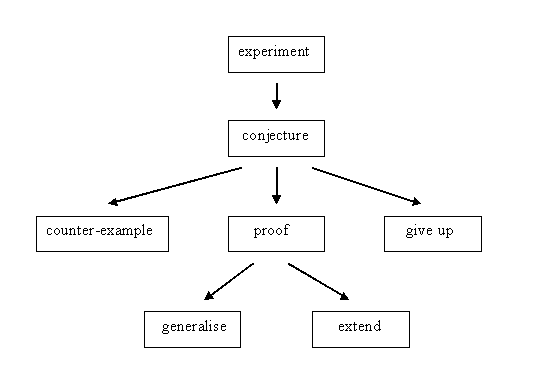
And now the cycle starts again. Each generalisation or extension leads to more experimenting, which leads to more conjectures, which leads …