“Think-alouds” (Davey, 1983) are used to model thinking processes. By verbalising his or her thoughts, a teacher can model the strategies they use to understand and solve problems. Thinkalouds help students to recognise that there are often a number of steps involved in tackling a problem and that answers don’t just magically appear.
Examples of strategies that can be modelled include using prior knowledge, drawing a diagram or using equipment, imaging, looking for patterns, and making predictions. The strategies the teacher models should be informed by the learning needs of the students.
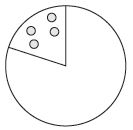
For example, a teacher wants a student to see how visualising the size of a share (in this case, a piece of cake) can be used to work out how many shares are needed to make a whole:
“Here is a piece of Rongopai’s birthday cake. Each piece of cake has the same number of candles. How old is Rongopai?”
Numeracy Development Projects Book 7, page 27
Well, I know that Rongopai’s age is the same as the number of candles there were on the whole cake, so that is what I need to work out.
First I need to find out how many pieces the cake was cut into. I know what a quarter looks like. It would look like this (the teacher traces a quarter shape on the circle). But this piece looks a bit smaller, so there must have been more than four pieces.
I can use my finger to trace where each cut was made. I’m estimating where each line would be, using the first piece as a guide, because all the pieces need to be the same size. The first line would be about here (the teacher traces a line with her finger), then one here and one here (tracing two more lines). Three lines. I can kind of “see” the lines and pieces in my mind. When I count back, there are four “invisible” pieces, plus the one drawn in. Five pieces. Phew! I’ll write that down so I don’t forget …
The teacher can ask the student to participate in the think-aloud by asking the student for suggestions. For example:
I know that there were five pieces. What shall I do next?
Back to Resource 6: Building understanding through effective questioning and modelling