Place value and multiplicative thinking are intricately linked. Central to both is the idea that a group of items can be a single entity (for example, one “hundred”) and that at the same time the group contains a number of objects (for example, one hundred represents ten 10s or 100 ones). Like multiplication, place value is built on the principle of groups of equal size. For example, 340 represents three groups of 100, and 4 groups of 10.
Place-value equipment can be used to strengthen this understanding of equal groups. For example, if a student needs to solve 3 x 26, they could use place-value blocks to make three groups of “two tens and six ones” then trade 10 ones to make an additional ten (3 x 26 makes 6 tens and 18 ones, which is 7 tens and 8 ones = 78).
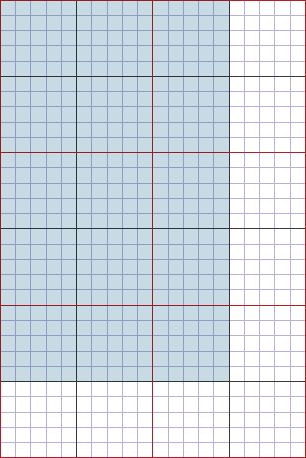
Using arrays to solve two-digit multiplication problems provides a visual model of 10 tens making one hundred. The following example is based on the grid in “Fostering Multiplicative Thinking Using Array-based Materials” (Young-Loveridge, 2005).
The grid is structured in blocks of 10 by 10 (red lines), each divided into 5 by 5 sub-blocks (grey lines).
Multi-digit multiplication problems up to can be shown on the grid. For example, here is 25 x 15:
The base-ten structure of the grid makes it easy to see the two blocks of 100, the three blocks of 50 (5 x 10) that together make another 150, and a block of 5 x 5 that completes the array. Summing the partial products (200 + 150 + 25) gives a total of 375, the product of 25 by 15.
The nzmaths website provides a number of activities that make links between place value and multiplication:
https://nzmaths.co.nz/resource/multiplying-tens
https://nzmaths.co.nz/resource/bean-counters
See also: