Big Idea
Decimals, fractions and percentages are closely related.
Background Points for teaching:
- Decimals are another way of writing fractions.
- Percentages are another way of writing hundredths.
- Students need to develop some fraction-decimal relationships as benchmarks.
Decimals are another way of writing fractions.
Because decimals are part of the base-ten place value system, the clearest connections between decimals and fractions occur where the denominator of a fraction is a power of ten:
1/10 = 0.1
3/100 = 0.03
6/1000 = 0.006
Place value materials can be used to support students to develop conceptual links between fractions and decimals.
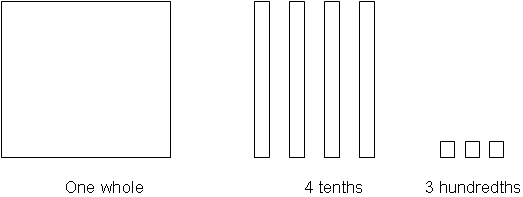
For example, the following representation shows both 1.43 and 1+ 4/10 + 3/100
There is a 10-to-1 relationship between the value of any two adjacent places in a number.
For example:
4 tenths = 40 hundredths
1.68 = 1 + 6/10 + 8/100
= 1 + 68/100
By applying place value it is simple to convert from a decimal to fraction. Understanding that the place to the right of the decimal point is the tenths place makes it immediately clear that, for example,
0.3 = three tenths = 3/10
0.47 = forty seven hundredths = 47/100
It is possible to convert fractions to decimals by (i) converting the denominator to a power of ten, or (ii) by using equivalent fractions or (iii) by using division. It is often more useful to work with numbers in the form of decimals than fractions.
- Fractions can be converted to a denominator of a power of ten:
3/5 = 6/10 or 60/100 = 0.6
- By using equivalent fractions it is possible to convert the fraction to a simple denominator that is then easily converted to a decimal. It is therefore useful to know some simple conversions between fractions and decimals.
3/12 = 1/4 = 0.25
- By using division a decimal can be found.
1/3 = 1 ÷ 3 = 0.33333.
Percentages are another way of writing hundredths.
The term percent is another name for hundredths. A fraction expressed as a hundredth can simply be renamed as a percent. For example, 1/4, or 25/100 is expressed as 0.25 and as 25%.
An understanding of the role of the decimal point in naming decimals can help in understanding the link between hundredths and percents. The decimal point identifies the units. So in the decimal 0.742 the decimal point identifies the unit of ones. The word ones is implied. It could also be written as 7.42 tenths of 74.2 hundredths. The term hundredths can be replaced with percent to be 74.2%. Further explanations of the decimal point in naming decimals can be found in the information on the Decimal Number System.
Percents can be represented pictorially in the same way as tenths and hundredths using base-ten models such as 10 x 10 grids and circular disks marked around the edge. Place value columns can also show the term percent.
| Ones | Tenths | Hundredths (Percent) |
Thousandths |
Students need to develop some fraction-decimal relationships as benchmarks.
To solve problems it is helpful for students to be able to interchange between fractions and decimal units. For example, if a student was to work out the saving of 25%, the conversion to a 1/4 would make the problem easier to solve. The benchmarks of 1/10s, 1/4s, 1/3s and 1/5s are useful to know after an understanding of the fraction-decimal relationship has been established.