The purpose of this activity is to engage students in evaluating powers of whole numbers and generalise the repeating sequence in the ones digit of those powers.
This activity assumes the students have experience in the following areas:
- Multiplication and division of whole numbers and decimals, including division with remainders.
- Evaluating powers of whole numbers, with whole number exponents.
- Continuing sequential patterns and finding rules for the next term.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
The last (ones) digit of 32 is 9 since 3 x 3 = 9
The last (ones) digit of 33 is 7 since 3 x 3 x 3 = 27
The last (ones) digit of 34 is 1 since 3 x 3 x 3 x 3 = 81.
What is the ones digit of 32019?
Do similar patterns exist in the powers of other whole numbers? For example, what is the ones digit of each of the following?
- 52019
- 22019
- 42019
- 82019
- 72019
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- What are the important words and symbols? (Students need to understand the meaning of powers expressed in exponent notation, e.g., 34 = 3 Х 3 Х 3 Х 3.)
- What would be good examples to try? (That involves replacing x with different whole numbers. The task suggests using 3, 5, 4, 8, and 7 as bases.)
- What do I already know that will be needed to solve this problem? (Students may recognise that the ones digit can only be predicted if there is a repeating pattern in the powers.)
- Can I imagine (visualise) what the numbers look like?
- What part of the problem could I get started with? (Working on one base to start with simplifies the task and enables pattern spotting. Once a pattern for one base is found, the strategy can be applied to powers of different bases.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What are the maths skills I need to work this out? (Multiplication and division are required to make sense of the patterns generated by powers. Looking for repetition in the powers is also required.)
- What could the solution look like? (The problem demands a rule to predict the ones digit of any power for a given base.)
- What strategies can I use to get started? (Listing many examples in sequence will help with pattern spotting.)
- Can I notice a pattern to write down and explore?
- What simple numbers, for the base, could I try first?
- What tools (digital or physical) could help my investigation? (Digital calculation will save time and ease load on working memory.)
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I created enough examples to find a common property among the differences?
- Have I recorded my ideas in a way that helps me to see patterns?
- Are there any patterns?
- How might I describe and represent the pattern?
- What is the best way to express the patterns I see? (Algebra is important to this task. Letters can be used as generalised numbers, e.g., X used to represent any base.)
- Can I express my rule for finding the ones digit as an algorithm (set of steps)?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is the solution?
- Show and explain how you worked out your solution.
- Is the solution (algorithm) the same or different for powers of each base? Why are the algorithms different?
- How does my solution answer the question? (Do my algorithms work reliably, or do they need refinement?)
- What connections can I see to other situations, why would this be? (Could students extend their reasoning to deal with ones digits for powers of other bases, such as 11, 13, and 27?)
- Do similar patterns exist in the tens, hundreds, thousands, … digits? Why or why not?
- Which ideas would convince others that my findings answer the investigation question?
Examples of work
Work sample 1
The student uses calculations, with the support of digital technology, to identify elements of repeat in the ones digit of powers.
Digital technology allows for powers to be calculated easily. Since the purpose of the task is for students to identify and apply sequential patterns, rather than perform mental or written calculations, it is appropriate that digital technology is freely available. For example, students can be asked to program a spreadsheet to calculate the powers of three. They might begin with a layout like this. Note that a recursive formula as shown will take the cell content above and multiply that number by three.
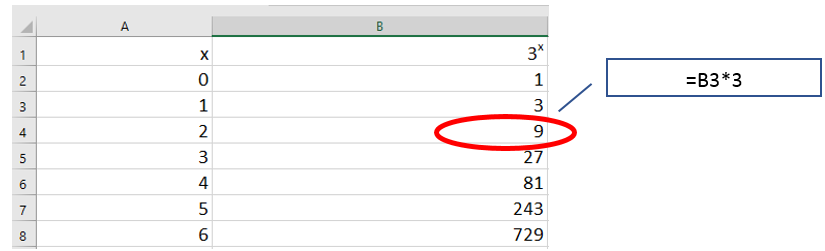
A limitation is that most spreadsheets limit the number of digits available in a cell to 15 or 16. That will mean that the display below occurs:
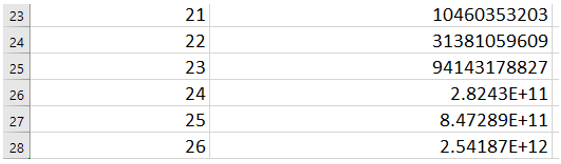
The limitation is good in that students will need to predict the pattern. Students should identify that the ones digits follow a repeating sequence 1, 3, 9, 7, 1, 3, 9, 7, …
Students can use their scientific calculator to though the same restrictions apply to the length of the number displayed. For example, 320 will display as 3486784401. However, 321 will not display correctly as it requires 11 digits. So even with support of digital technology students need to apply a conceptual approach to find the ones digit of 32019.
Work sample 2
The student uses multiplicative thinking, particularly division with remainders, to predict the ones digit of powers.
Click on the image to enlarge it. Click again to close. 
Therefore, 32019 will have 7 as the ones digit because 32020 will have 1 as the ones digit, since 2020 is divisible by four (remainder zero).