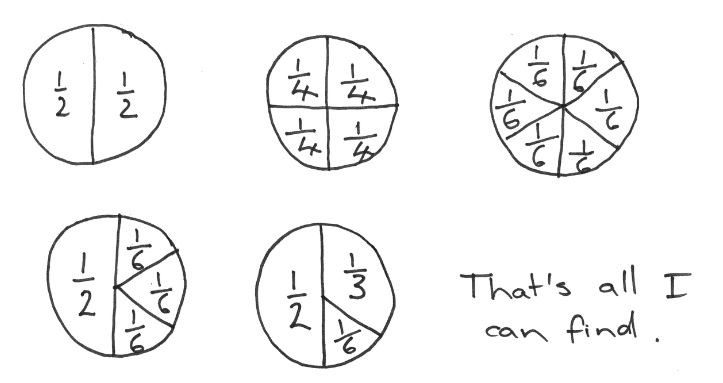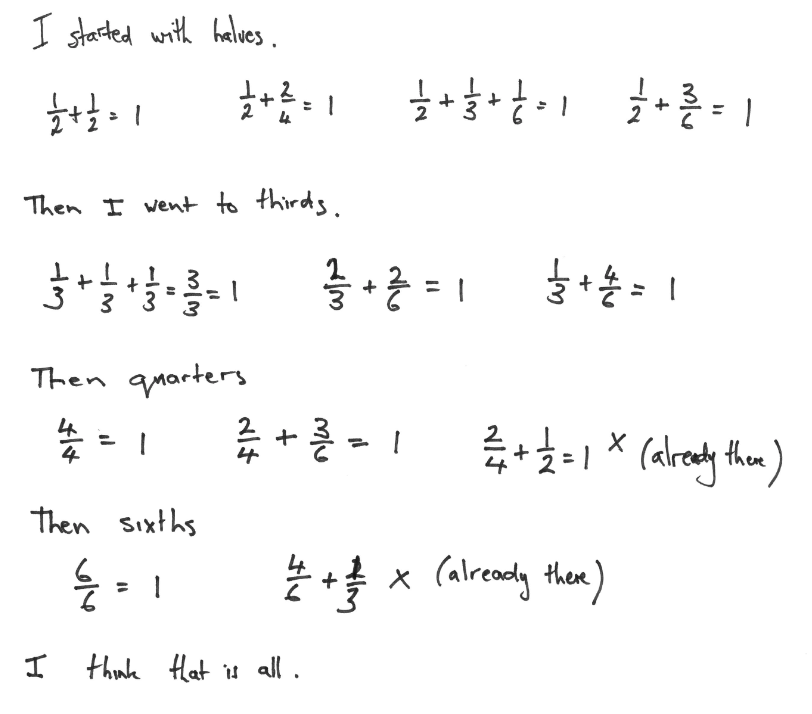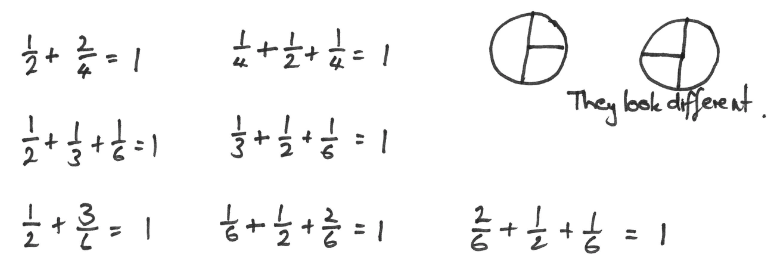The purpose of this activity is to engage students in finding many ways to form one (whole) with fractional units. In doing so they will use simple equivalence and learn to recognise non-unit fractions as iteration of unit fractions.
This activity assumes the students have experience in the following areas:
- Partitioning shapes into equal parts.
- Form the whole when given a fraction part.
- Represent a part-whole relationship as a fraction.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
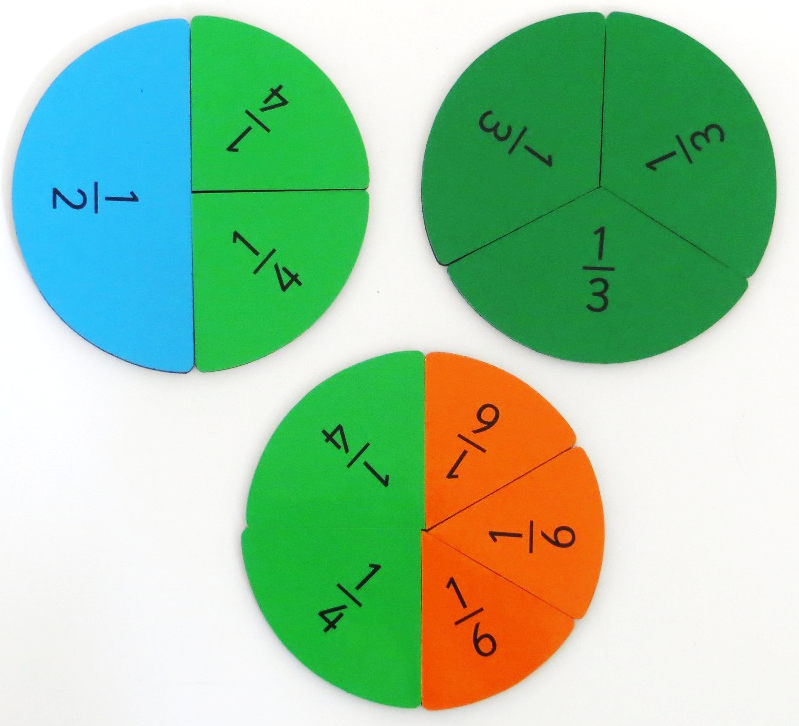
Here are three ways to make one (whole) with halves, thirds, quarters and sixths of a circle.
How might these ways to make one be recorded as equations or expressions?
What other ways to make one can you find just using halves, thirds, quarters and sixths?
Can you prove you have found all the possible ways?
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand the situation and the words? (Students must understand that they are using a restricted set of unit fractions to make one whole (circle).)
- What are the important words and symbols? (The meaning of fraction terms like sixths and thirds needs to be understood. Equations have an equal sign, e.g., ½ + 1/3 + 1/6 =1.)
- Can I make one using just one size of fraction piece? (3/3 and 4/4 are names for 1.)
- What will my solution look like? (The solution will provide a set of ways to make one with the given pieces. It might also include a justification that all the possible ways are found.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What are the maths skills I need to work this out?
- What tools might be useful? (A set of fraction circles will be helpful.)
- How will I record the ways to make one?
- What strategies can I use to get started?
- Can I notice a pattern to write down and explore?
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Am I showing my workings in a way that helps me see patterns?
- Do my answers seem correct? How can I check?
- What strategy am I using to find as many ways as possible?
- Have I found all the possible ways? How do I know?
- How could I make sure that I haven’t missed anything?
- Does my solution answer the question?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is the solution?
- Is my working clear for someone else to follow?
- How would I convince someone else I am correct?
- How will I convince someone that I found all the possible ways to make one?
- Could I have solved the problem in a more efficient way?
- What could I find out next?
Examples of work
Work sample 1
The student uses trial and error approaches to find other ways to make one.
Click on the image to enlarge it. Click again to close.
An improvement is to name iterations of unit fractions as non-unit fractions, like this:
Click on the image to enlarge it. Click again to close.
Work sample 2
The student uses a systematic strategy to find all the possible ways to make one and uses expressions or equations to record the ways.
Click on the image to enlarge it. Click again to close.
Some students may consider order relevant in establishing unique names for one. That assumption will increase the number of possible ways they find.