This unit integrates the mathematics and science learning areas, and provides an opportunity for students to explore the context of chemical reactions involving common household acids and bases. In turn, students will develop their use of rates and ratios, and will explore linear relationships using tables and graphs.
- Identify household acids, bases, and neutral solutions, and pH indicators.
- Construct a pH indicator scale.
- Construct appropriate and accurate graphs.
- Interpret and apply graphed results of a practical investigation.
The activities in this unit develop students' mathematical skills and knowledge, relevant to their multiplicative thinking and understanding of patterns and relationships, in the context of science (understanding the material world; investigating the chemical properties of acids and base).
Within this, students utilise a scientific investigation to model a real life situation. This includes the following key understandings:
- measuring and recording data to find the relationship between two variables
- recognising a pattern, from a table and/or a graph, and describing it as being linear (or not)
- plotting a linear relationship on an appropriate set of axes
- describing the key features of a graph
- generalising the pattern
- forming a rule from which predictions can be made and tested
- solving problems using the relationship shown on a graph and/or described by an algebraic equation.
Note that the context of neutralising acids and bases does not yield the exact linear relationships hinted at in this unit, but does so approximately when only strong acids and bases are used. It can be argued that students will gain a better understanding of chemical processes overall, if they can first look for clear patterns in such constrained settings.
The work outlined in the practical activities requires solutions and equipment that should be available in secondary school laboratories. You will need to have access to the expertise of a science teacher (or other, knowledgeable community members) and the resources necessary for this practical work.
This cross-curricular, context-based unit has been built within a framework that has been developed, with input from teachers across the curriculum, to deliver the mathematics learning area, whilst encouraging differentiated, student-centred learning.
The learning opportunities in this unit can be further differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- roaming and supporting students in a variety of groupings to ensure they understand the task at hand, the skills needed to succeed, and can apply these skills in a suitable process
- varying the amount of structured scaffolding and guided teaching you provide to students when investigating new tasks
- providing opportunities for students to create their own problems, ideally related to a familiar, relevant context (e.g. bee stings)
- providing extended opportunities for students to revise and apply learning from throughout the unit
- modelling the application of ideas at every stage of the unit
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- allowing the use of calculators to reduce the cognitive load required in each task
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities (e.g. creating a graph).
With student interest engaged, mathematical challenges often seem more approachable than when presented in isolation. Therefore, you might find it appropriate to adapt the contexts presented in this unit.
Structure
The first session is an introductory activity that is aimed to spark the imagination of students, to introduce the need for a particular idea or technique in mathematics that would enable them to explore deeper into that context. It is expected that rich discussion may be had around the context and around the nature of the mathematics involved.
Following the introductory session, each subsequent session in the unit is composed of four sections: Introducing Ideas, Building Ideas, Reinforcing Ideas, and Extending Ideas.
Introducing Ideas: It is recommended that you allow approximately 10 minutes for students to work on these problems, either as a whole class, in groups, pairs, or as individuals. Following this, gather the students together to review the problem and to discuss ideas, issues and mathematical techniques that they noticed during the process. It may be helpful to summarise key outcomes of the discussion at this point.
Building Ideas, Reinforcing Ideas, and Extending Ideas: Exploration of these stages can be differentiated on the basis of individual learning needs, as demonstrated in the previous stage of each session. Some students may have managed the focus activity easily and be ready to attempt the reinforcing ideas or even the extending ideas activity straight away. These could be attempted individually or in groups or pairs, depending on students’ readiness for the activity concerned. The students remaining with the teacher could begin to work through the building ideas activity together, peeling off to complete this activity and/or to attempt the reinforcing ideas activity when they feel they have ‘got it’.
It is expected that once all the students have peeled off into independent or group work of the appropriate selection of building, reinforcing and extending activities, the teacher is freed up to check back with the ‘early peelers’ and to circulate as needed.
Importantly, students should have multiple opportunities to, throughout and at the conclusion of each session, compare, check, and discuss their ideas with peers and the teacher, and to reflect upon their ideas and developed understandings. These reflections can be demonstrated using a variety of means (e.g. written, digital note, survey, sticky notes, diagrams, marked work, videoed demonstration) and can be used to inform your planning for subsequent sessions.
The relevance of this learning can also be enhanced with the inclusion of key vocabulary from your students' home languages. For example, te reo Māori kupu such as āwhata (scale), āwhata pH (pH scale), kauwhata (graph), and tūhuratanga ā-ringa (practical investigation) might be introduced in this unit and then used throughout other mathematical learning.
- Suitable quantities of water that was used to cook red cabbage (or water and red cabbage), vinegar, baking soda, lemon juice, dishwashing liquid, soda water, fizzy tablet, hand soap, laundry detergent, shampoo, apple juice
- Test tubes and racks
- Droppers
- Spatulas
- pH strips (optional)
- 50mL containers
- Measuring scales
- Squared paper
- Recording tables and templates
Introductory session
This activity is intended to motivate students towards the context and to inform teachers of students' understandings.
- Pose the following problem to students.
The Bee Sting Problem:
One summer’s day Charlie’s little sister Lilly comes running into the house, crying. She has been stung by a bee! There is no consoling Lilly. Charlie remembers something he heard once about how he can add some household ingredient to take the pain away...but what was it? And why? And how much?
What can you find out about bee stings?
- Are they acidic or basic?
- Would an acid or a base need to be applied to ‘neutralise’ the bee sting?
- Are there any products that could neutralise a bee sting that may be commonly found at home?
Session two
This session focuses on learning about household acids, bases, and neutral solutions.
Introducing Ideas
- Explain to students: We can measure how acidic or basic a solution is using an acid-base indicator. One indicator can be made from the water that was used to cook red cabbage. Strain the juice after cooking, and leave this coloured water to cool for an hour. Acids and bases will each turn this cabbage juice indicator a different colour.
- Test water and solutions of vinegar, baking soda to find what colour the juice goes when a solution is neutral, acidic or basic.
Building Ideas
- White vinegar is acidic. Put a finger height of white vinegar in a clean test tube and note the colour of this solution. Add a few drops of cabbage juice indicator to the vinegar. Note the colour change.
- What colour is the cabbage juice indicator when it is in an acidic solution?
- Baking soda is basic. Dissolve a spatula full of baking soda in water, in a clean test tube and note the colour of this solution. Add a few drops of cabbage juice indicator to the baking soda solution. Note the colour change.
- What colour is the cabbage juice indicator when it is in an basic solution?
- Water is neutral. Put a finger height of water in a clean test. Add a few drops of cabbage juice indicator to the water. Note the colour change.
- What colour is the cabbage juice indicator when it is in a neutral solution?
Reinforcing Ideas
Make up solutions of each of the following and test with cabbage juice indicator to decide whether they are acids, bases or neutral:
- Lemon juice
- Dishwashing liquid
- Soda water
- Fizzy tablet
- Hand soap
- Laundry detergent
- Shampoo
- Apple juice
Extending Ideas
From your research you have learned that bee stings are acidic.
- What could you do to neutralise the acidity of Lilly’s bee sting?
- Suggest an emergency procedure for neutralising a bee sting using common household products.
- Use cabbage juice indicator to test whether these products are acids or bases.
- How could you be sure that the sting site was neutralised and no longer acidic, nor made basic?
Session three
This session focuses on learning about pH indicators.
Introducing Ideas
- Explain to students: Charlie has learned that bee stings are acidic. He knows that applying the appropriate amount of a base will neutralise the acid of the sting. To be sure of how much of a basic solution is needed to neutralise the sting, Charlie needs to know more about measuring acidity. Acids, bases and neutral solutions are all measured on the pH scale.
The concentration of hydrogen ions (H+) in a solution is measured on a scale called pH. An acid solution has a pH of < 7, a basic solution has a pH of > 7. We have found that cabbage juice indicator goes pink-red-crimson-purple in acid solutions, purple in neutral solutions and blue-green-yellow in basic solutions.
The graph below shows the how the concentration of hydrogen ions (H+) in a solution relates to the pH of that solution.
- Mark the regions of the graph in which a solution would sit if it:
a) Turned cabbage juice indicator yellow
b) Turned cabbage juice indicator pink
c) Turned cabbage juice indicator purple
d) Turned cabbage juice indicator green
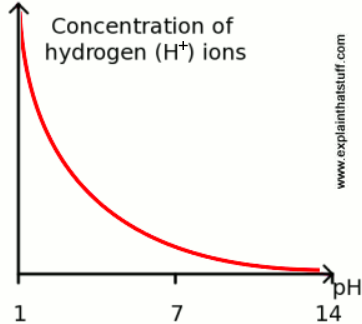
The pH scale goes from 1-14, representing the concentration of hydrogen ions (H+) in a solution. A solution which has a pH of 1 has 10x more hydrogen ions (H+) than the same volume of a solution of pH of 2. A solution which has a pH of 1 has 100x more hydrogen ions (H+) than the same volume of a solution of pH of 3.
Building Ideas
- Provide time for students to work through the following problems:
- Which solution, a solution of pH = 2 and and solution of pH = 3 has a higher concentration of hydrogen ions?
- Which solution, a solution of pH = 5 and and solution of pH = 3 has a higher concentration of hydrogen ions?
- Which solution, a solution of pH = 7 and and solution of pH = 3 has a higher concentration of hydrogen ions?
Reinforcing Ideas
- Provide time for students to work through the following problems:
- How does the concentration of hydrogen ions in a solution of pH = 3 compare with the concentration of hydrogen ions in a solution of pH = 5?
- How does the concentration of hydrogen ions in a solution of pH = 3 compare with the concentration of hydrogen ions in a solution of pH = 7?
- How does the concentration of hydrogen ions in a solution of pH = 3 compare with the concentration of hydrogen ions in a solution of pH = 10?
Extending Ideas
- Provide time for students to work through the following problems:
- How does the concentration of hydrogen ions in an acidic solution of pH = 1 compare with the concentration of hydrogen ions a neutral solution?
- How does the concentration of hydrogen ions in an acidic solution of pH = 1 compare with the concentration of hydrogen ions a basic solution of pH = 8?
- Describe the relationship between the concentration of hydrogen ions in an acidic solution of pH = 1 and the concentration of hydrogen ions a solution of pH = n (where n may be 1, 2, 3, …14)?
This activity aims to develop students’ understanding of a science concept through interpretation of a mathematical relationship displayed on a graph. The relationship itself is exponential, but is applicable for students working at level 4 of mathematics in the NZC because the numbers are used are whole numbers from 1-14 and the powers of ten.
Session four
This session focuses on making a pH indicator scale.
Introducing Ideas
- Explain to students: Charlie wants to treat his sister Lilly’s bee sting. He knows that applying the appropriate amount of a base will neutralise the acid of the sting. Charlie has been looking at how we measure acidity. Now he needs to work out just how much of a basic solution to is needed to neutralise Lilly’s sting.
- Explain the next stage of the task to students:
- Working in small groups, students are to gather 6 test tubes on a rack and 3 droppers.
- They also need 50mL of each of the following solutions; cabbage juice indicator, vinegar (acetic acid) and dissolved baking soda. Students should use one dropper for each of these solutions and be careful not to mix the droppers up.
- Students need to add 10 drops of vinegar (acetic acid) to one test tube, and add 5 drops of cabbage juice indicator. This is the acid ‘control’. This should be stored on the far left of the test tube holders. This is the colour of the acid.
- Students need to add 10 drops of neutral cabbage juice to a test tube and store this test tube on the far right of the test tube holder. This is the colour of the neutral.
- Pose the following questions to students:
- Which test tube represents a bee sting? What colour is the indicator in this solution?
- What are we using as a base to neutralise the bee sting?
- Which test tube represents a neutralised bee sting? What colour is the indicator in this solution?
- With the four remaining test tubes, students are to add the following.
- 5 drops of vinegar, 5 drops of indicator
- 10 drops of vinegar, 5 drops of indicator
- 15 drops of vinegar, 5 drops of indicator
- 20 drops of vinegar, 5 drops of indicator
Building Ideas
- To each test tube, students are to carefully add one drop at a time of baking soda until the solution just turns purple neutralised (purple). They should count and record the number of drops of baking soda that could be added to the test tube until it was purple
Reinforcing Ideas
- To each test tube, students are to carefully add one drop at a time of baking soda until the solution is neutralised (purple). They should record the number of drops of baking soda solution that could be added to the test tube until it was purple. One more drop would make it go blue and be one drop too many. If a student's solution turned purple with x drops of indicator, they should record the number needed to neutralise as x – 1.
Extending Ideas
- To each of the four test tubes, students should add just enough baking soda solution to neutralise the solution in that tube. They should record the results so that they will be able to graph the volume of vinegar against the volume of baking soda solution needed to produce a neutral solution.
This activity has an emphasis on practical technique for science, with the need for careful measurement and recording being a major outcome. Encourage students to take accurate measurements and to record their results in a table. If time and resources allow, they should repeat the procedure several times so that they may use the average of their individual results for each test tube.
Session five
This session focuses on students graphing the results of their practical investigations.
In session four, students gathered data from a practical investigation, measuring the quantity of a given basic solution needed to neutralise an acidic solution. This investigation was modelling how much of a sting treatment (base) would be needed to to neutralise different amounts of a bee sting (acid).
Introducing Ideas
- With students, look at the results from the practical work in session four. Consider the following points as a class:
- Do you expect every group to have similar or different results?
- If we graph these results, how many data points would there be for one group’s results?
- What will the labels of the axes of this graph be?
- What shape do you think these data points would form when they are graphed?
Building Ideas
- Together, construct an appropriate graph:
- On squared paper, rule a set of axes
- Label the horizontal axis number of drops of vinegar (the independent variable)
- Label the vertical axis with number of drops of baking soda solution (the dependent variable)
- Choose a suitable scale for each of your axes
- Plot the data you recorded from the investigation.
Reinforcing Ideas
- Have students independently construct an appropriate graph following the process below:
- On squared paper, rule a set of axes
- Choose a suitable scale for each of your axes. The independent variable will be on the horizontal axis.
- Plot the data you recorded from the investigation.
Extending Ideas
- Have students consider the following prompts:
- What type of relationship is shown on this graph?
- Think about the range of the data. If this graph is extended to show all the possible results, should this be done with more dots (discrete data) or would it be appropriate to fit a line (continuous data)?
Session six
This session focuses on interpreting and applying graphed results of a practical investigation.
In session five, students graphed their data from a practical investigation, measuring the quantity of a given basic solution needed to neutralise an acidic solution. This investigation was modelling how much of a treatment (base) would be needed to to neutralise different amounts of a bee sting (acid). Their graphs should show a linear relationship between the amount of sting (acid) and the amount of treatment (base) needed to neutralise the sting.
Introducing Ideas
- Support students to interpret their graphs (from session 5) using the following prompts:
- What type of relationship is shown in your graph?
- Describe the relationship you have discovered by graphing your results.
- Using a for the sting (acid, vinegar) and b for the treatment (base, baking soda solution), write an equation to show the relationship between b and a.
Building Ideas
- Pose the following scenario to students: After taking Lilly to the doctor, Charlie has discovered that the unusual bee that stung Lilly actually injected 30 drops of venom when it stung Lilly! This is a rare bee indeed!
- Use your graph to tell Charlie how much baking soda solution he needs to add to perfectly neutralise the bee sting and make Lilly’s pain go away.
Reinforcing Ideas
- Pose the following scenario to students: After taking Lilly to the doctor, Charlie has discovered that the unusual bee that stung Lilly actually injected 37 drops of venom when it stung Lilly! This is a rare bee indeed!
- Can you figure out how to help Charlie? How much baking soda solution does he need to add to perfectly neutralise the bee sting and make Lilly’s pain go away?
Extending Ideas
- Pose the following scenario to students: After taking Lilly to the doctor, Charlie has discovered that the unusual bee that stung Lilly actually injected n drops of venom when it stung Lilly! This is a rare bee indeed!
- Can you figure out how to help Charlie? How much baking soda solution does he need to add to perfectly neutralise the bee sting and make Lilly’s pain go away?
This session focusses on the generalisation and application of a linear relationship. Because the relationship has been derived from a practical context, students should be well placed to discuss the domain and range of the relationship. Looking at the shape of the graph, they should recognise a linear trend. Their data may not fit exactly along the trend-line, which will give the opportunity to discuss experimental uncertainty and the accuracy of their measurements. Discussion could compare the relative merits of using their graph (interpolation, extrapolation) with the use of the algebraic rule of the trend-line to solve a problem.
Dear families and whānau,
Recently, we have been developing our use of rates and ratios, and exploring linear relationships using tables and graphs, in the context of chemical reactions involving common household acids and bases. Ask your child to share their learning with you.