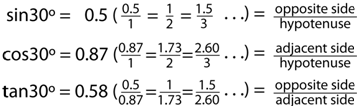The key idea of transformation at level 5 is that changes to an object under different transformations can be calculated.
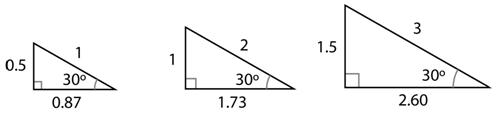
At this level, the invariance of the internal angles of a shape under enlargement (object and image are ‘similar’) is used as the basis for exploring the trigonometric ratios of right angled triangles. For example, all of the ratios of side lengths of these triangles are equivalent fractions because the triangles are similar:
For a right angled triangle where one of the angles is 30º, the trigonometric ratios shown in the above diagram are:
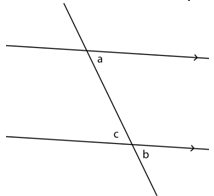
Translation, rotation and reflection can also be used to identify the relationships between alternate angles and corresponding angles produced by a line transversing two parallel lines. In the following diagram angle a transforms to the position of angle b by translation. Angles under translation are invariant, so a = b. Angle a transforms to angle c by rotation, and angles under rotation are invariant, so a = c.
Proportional reasoning is important at this level. An example of this is the relationship of various attributes of a 3-dimensional shape under enlargement, as illustrated in the following table where the object has been enlarged by scale factor ‘n’:
| length of sides | area of faces | volume of shape |
| original x n | original x n2 | original x n3 |
This key idea develops from the key idea of transformation at level 4 idea that some properties of objects do not change under different transformations.
This key idea is extended to the key idea of transformation at level 6 that there is more than one way to achieve the result of a given transformation.