The key idea of transformation at level 3 is that specific items are needed to describe different transformations.
At level 3 students are developing their ability to accurately describe the effects of transformations, using for example, mirror lines for reflection, and centres and scale factors for enlargement.
Enlargement is a transformation that changes the size of objects. Enlargements are specified by the position of the centre of enlargement and the scale factor. For example, a scale factor of two will result in an object which is twice the size of the original. Scale factors of less than one result in figures that are smaller than the original. While these are not frequently used at this level, negative scale factors result in an object ‘reflected’ on the other side of the side of the centre of enlargement.
Under enlargement the original object and the enlarged object are said to be similar. That is, all their corresponding angles are congruent, and the lengths of their corresponding sides are proportionally related. In comparison, two objects are described as congruent if they are the same size and shape.
Reflections can be described by the position of the line of reflection (mirror line). Each point in a reflection is the same distance from the line of reflection, but on the opposite side, from the corresponding point in the original object.
Rotations can be specified by the angle of rotation and the location of the centre of rotation.
Translations can be described in terms of the direction and distance moved (for example a translation of 3.2cm at a 45 degree angle), or as movement along the x and y axis.
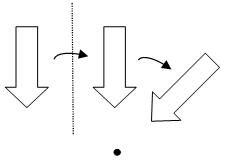
Transformations can be composed; that is transformations can be carried out in succession. For example, the arrow in the left of the diagram below has undergone a reflection through a vertical line to the right of the arrow, and the result of this has been rotated by 45degrees around a point directly below the tip of the arrow. 
This key idea develops from the key idea of transformation at level 2 that some objects have symmetry and do not change position or appearance under some transformations.
This key idea is extended to the key idea of transformation at level 4 that some properties of objects do not change under different transformations.
The Ministry is migrating nzmaths content to Tāhurangi.
Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).
When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.
e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available.
For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths