The key idea of transformation at level 2 is that some objects have symmetry and do not change position or appearance under some transformations.
There are two types of symmetry:
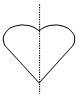
- Line symmetry: A shape that can be folded down a line to produce two matching halves is said to have line symmetry. The fold-line is called a line of symmetry. A line of symmetry can also be described as a mirror line or line of reflection because the part of the object that is on one side of the line is reflected onto the other side of the line. If an object is reflected across a line of symmetry its appearance does not change.
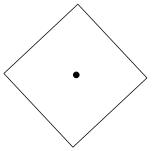
- Rotational symmetry: An object is said to have rotational symmetry if it can be rotated around a point so that it looks the same as it did before the rotation. The number of times an object can be fitted back onto its original outline during one complete turn is called the object’s order of symmetry. If an object with rotational symmetry is rotated around it’s centre, by an appropriate angle, its appearance does not change. For example, if the diamond below is rotated around its mid-point by 90, 180, 270 or 360 degrees, its appearance remains the same.
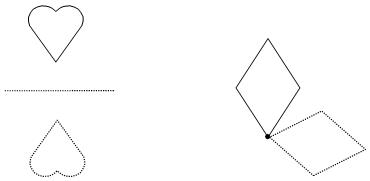
The appearance of a shape after a transformation is dependent not only on the type of transformation but also on where the lines of reflections or points of rotation are placed. The diagram below show instances where the position and appearance of objects are changed under reflection and rotation.
Because translation involves simply sliding an object, objects that have undergone translation do not change their appearance.
This key idea develops from the key idea of transformation at level 1 idea that the position and appearance of an object can be changed by reflecting (flip), translating (slide), and rotating (turn).
This key idea is extended in the key idea of transformation at level 3: that specific items such as mirror lines and scale factors are needed to describe different transformations.