X-ray Vision

No single view of a solid object will give us all the information we need in order to construct it. As the students will discover from this activity, even four views may not be enough to define a unique structure.
One approach to question 1 is to use trial and improvement. The students can use cubes to make the simplest possible model that fits the front view and then adjust the design until it also conforms with the other views.
Another approach is for them to see how much information they can deduce from the four views before they begin:

•  The building is no more than 3 cubes wide, deep, or high.
•  There is only 1 cube in the top layer, and it is in the back right-hand corner.
•  The front of the building is 1 cube high, and the next row back is 2 cubes high at some point.

The Answers show three ways of making a model with 12 cubes, but there are other possibilities. The studentscould see how many they can find, using square grid paper to keep a record of their designs. They could then get a classmate to check their designs. Challenge them to do the checking without first seeing the madeup
model.
Questions 2b and 3c involve isometric drawing. Students usually find it easy to learn this drawing technique, but if yours have not met it before, you should spend some time introducing it. Some practical tips include:

•  Use the isometric dot paper the right way up. (The dots should form vertical lines.)
•  Turn the object to be drawn so that the focus is on a vertical line (not a face).
•  There are four possible views of an object sitting on its base (one for each of the vertical edges of a cube).
• Choose the view that best reveals the structure of the object.
• Only draw the edges that you can actually see from your viewing angle.
• Only draw the edges of cubes if 2 different faces meet at that edge.
• Only use pencil and have an eraser handy.
• Render (shade) the 3 planes (left, right, and top) differently. This will help the viewer to visualise the 3-D nature of the object.

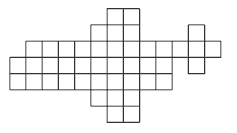
When drawing the net for question 2c, the students could begin with the 3-by-3 base, work outwards from there in 4 directions to get the sides, and then decide which side(s) they wish to attach the top parts to. As is usually the case with nets, there are many variations possible.
To build the model in question 3a, the students can hold their earlier version at eye level and remove cubes one at a time, checking to see that they are not changing any of the four profiles.
In question 4, it is possible to construct a model with 8 cubes, but if it were a real building, it would consist of three independent buildings touching at the corners, with no internal access linking them.
As a further task, you could challenge your students to construct another model, draw the 4 views (excluding the bird's-eye view), and get a classmate to make it with as many and as few cubes as possible.

Answers to Activity

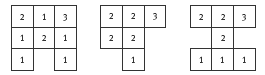
1. Practical activity. There are many buildings that will fit the given views. Three possibilities are:

(The numbers give the height, in cubes, of each level.)
2. a.

b.

c. Here is one way of constructing the net. There are many other possibilities.

3. a. Practical activity
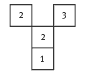
b. A bird's-eye view of the building would look like this:

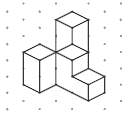
c. A drawing on isometric dot paper would look like this:

4. Yes, an 8-cube building could be constructed by cutting out the single cube at the centre back. But this would leave three groups of cubes that are not physically connected to each other: