This unit looks at two general equations associated with a sequence or pattern: (i) recurrence relations as general ways to see what happens between consecutive terms of a sequence; and (ii) the general term of a sequence as a function of the number of that term. The work in this unit is valid for any arithmetic progression, that is, any sequence where the difference between any pair of consecutive terms is the same.
- find the recurrence relation for simple sequences
- construct tables of values for a pattern
- find the value of the general term of a sequence algebraically
- find the value of the general term of a sequence geometrically
Recurrence relations: Implicitly, recurrence relations are probably the first thing that students use when they are dealing with patterns. It seems that it is easier to see the difference(s) between consecutive terms of a pattern than to see the general term. This is because the difference pattern is simpler than the original pattern. For instance, in patterns involving quadratic equations, the recurrence relation involves just a linear relation.
So what is a recurrence relation? It is just an equation that links a number of terms of a pattern. Here we will restrict it to mean the general relation between any pair of terms. For instance, in the sequence 4, 5, 6, 7, …, the difference between any two terms is 1. So if f(n) is the value of the n-th term of the pattern/sequence, then f(n) = f(n-1) + 1.
At this point it is worth noting that we will use f(n) for the general term of the sequence here. You may prefer to use Tn or some other notation.
Back to recurrence relations, any arithmetic progression where the difference between consecutive terms is d, has recurrence relation f(n) = f(n-1) + d.
Although we only worry here about recurrence relations that involve two terms, it is interesting to note that the Fibonacci sequence has recurrence relation f(n) = f(n-1) + f(n-2).)
Furthermore, with this type of recurrence relations, if we know the recurrence relation of a sequence and we know its first term, then we know the sequence completely. This is because we can start with the first term and then generate each successive term by applying the recurrence relation.
So if we are given f(n) = f(n-1) + 1 and f(1) = 2, we get 2, 3, 4, ..., and if we are given f(n) = f(n-1) + 1 and f(1) = 4, we get 4, 5, 6, …. So the initial term plays an important role in the sequence.
The problems with guessing: It is important to note that students often start off with a table of values for a ‘physical’ situation and then ‘guess’ the general term. This guess may not be correct. For instance we were working with students with a pattern that started out as 8, 48, …. One group guessed a pattern of 8 × 6n-1. While this fits the two values that they had found exactly, it is not the general term of the pattern they were investigating. Because they had failed to look for more terms, or to see the actual physical situation was changing, they went off in the wrong direction. The same thing can happen with the problem situations here. Therefore, it is important that recurrence relations are grounded in an actual physical problem, and not in a table of values that may be guessed from small values of the physical pattern.
Algebra versus geometry: We have taken two approaches to the general term here. This is done to present students with a variety of representations of the general term, and to enable students to see that there is more than one way to approach a problem.
Our algebraic approach works by using patterns, where the general term is a multiple of n, and inserting an extra column in our table between the number of the term and the value of that term. We then divide the number into the value to find a result.
The geometric approach relies less on guess work. Patterns such as the ones that we are working with here can be represented as rectangles – at least, they can when we put two of them together. This approach works for arithmetic progressions and related sequences.
The patterns of this unit: We look at five patterns here that we have called Barrels, Odd Bricks, Even Bricks, Dominoes and House of Cards (see Copymasters 1.1 to 1.5). We’ll discuss Barrels first and then see that the others are essentially the same.
The sequence that we get with Barrels is 1, 3, 6, 10, and so on. You might recognise these as being numbers in Pascal’s Triangle – take the diagonal that starts three ones down from the top. But because the rows of the n-th term have 1, 2, 3, 4, …, n barrels, the n-th term of the barrels sequence is actually the sum of the first n whole numbers. So to find the number of barrels in the n-th term we just have to add the first n whole numbers. This is the method we exploit in the geometric method of Sessions 3.
Odd Bricks goes 1, 4, 9, …. Clearly these are just the square numbers so it’s not too hard to find the n-th term. But how do we make up the n-th element? We simply add 1 to 3 to 5 to …. So the n-th term is just the sum of the first n odd numbers.
The n-th term of the Even Bricks’ sequence is the sum 2 + 4 + 6 + … + 2n; the n-th term of the Dominoes’ sequence is the sum 3 + 5 + 7 + … + (2n + 1); and the n-th term of the House of Cards’ sequence is the sum 2 + 5 + 8 + … + (3n – 1).
All of the n-th terms here are the sums of arithmetic sequences or arithmetic progressions. The elements of the sums increase by a constant, d, as n increases each time. We summarise each of these below.
| pattern | First term | d | General term | Sum = n-th term of the pattern |
| Barrels | 1 | 1 | n | n(n+1)/2 |
| Odd Bricks | 1 | 2 | 2n - 1 | n2 |
| Even Bricks | 2 | 2 | 2n | n(n + 1) |
| Dominoes | 3 | 2 | 2n + 1 | n(n + 2) |
| House of Cards | 2 | 3 | 3n - 1 | n(3n + 1)/2 |
So the n-th term of each of these patterns can be found if you know how to sum an arithmetic progression. And this sum is just the sum of the first and the last terms by the number of terms divided by 2. And it’s the fact that the difference between each term of the sum is the same that enables them to fit together so nicely for the geometric argument of session 3.
Incidentally, Odd Bricks, Even Bricks and Dominoes all have the same recurrence relation but have different initial terms. This underlines the fact that a sequence of numbers needs both a recurrence relation and an initial term to be specified before it is defined uniquely.
Where to next?: This whole area leads out in many directions. As we said earlier, it is easier for students to find recurrence relations for patterns than it is for them to find general terms. This is often the case for researchers too. But general terms are obviously more useful. Hence researchers have found ways to obtain general terms directly from recurrence relations. General terms for the recurrence relations of this unit can be found by solving appropriate quadratics. There are also things called generating functions that come in handy for a broader range of situations.
Anyone interested in these developments should read books on a topic called Combinatorics. It’s an essential part of a lot of what is known as Discrete Mathematics. The area has an increasing number of valuable applications to increasingly complex situations. Colleges in the USA generally have a course in these topics so it’s easy enough to find a book on the area or to find information on the internet.
The learning opportunities in this unit can be differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- providing extended opportunities to explore, construct, deconstruct, and discuss the patterns and sequences in each lesson
- using symbols alongside physical and diagrammatic models
- asking predictive questions to encourage students to think beyond what is visible
- providing opportunities for students to work in a range of flexible groupings to encourage peer learning, scaffolding, and extension
- modelling and providing explicit teaching at each stage of the unit. Gradually releasing your level of responsibility allows you to scaffold students towards working independently.
The focus of this unit is not related to a specific, real-world context. However, as a class, you might consider contexts that are reflected in each of the patterns and sequences presented (e.g. the building of a wall for a school buildings, stacks of cans of fizzy drink at a school event). Furthermore, at the conclusion of this unit, you may wish to explore real world applications of recurrence relations, and the general term of a sequence as a function of the number of that term.
Te reo Māori kupu such as tauira (pattern), raupapa (sequence), whārite (equation), and tūtohi (table (of data), chart) could be introduced in this unit and used throughout other mathematical learning.
- Copymasters 1.1, 1.2, 1.3, 1.4, 1.5 (various physical situations that give rise to interesting patterns)
- Copymasters 2.1, 2.2, 2.3, 2.4, 2.5 (tables from which to find the general term of the pattern)
- Copymasters 3.1, 3.2, 3.3, 3.4, 3.5, 3.6 (geometrical approaches to finding the general term for the Barrels and Odd Bricks prob
See the bottom of the unit for links to each Copymaster.
Session 1
In this session we take a look at several pattern situations. The aim here is to see that recurrence relations can be used to describe patterns and that tables can be generated by using these recurrence relations. The material in this session may take up to two lessons. You may decide that there are more situations here than you want to use in this unit.
Note that we have used f(n) to denote the n-th term of a sequence.
- You might like to work the first pattern situation through as a whole class activity. This will help the students to see what you are trying to achieve with this work and how they might go about it.
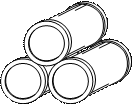
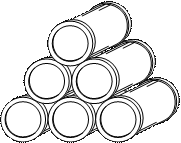
Consider Pattern 1: Barrels. We show a picture of the situation below (also available in Copymaster 1.1)
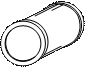
- How many barrels are there in the first picture? Call this f(1).
- How many barrels are there in the second picture? Call this f(2).
- How many barrels are there in the third picture? Call this f(3).
- If the pattern goes on like this, how many barrels are there in the tenth picture? Call this f(10).
- How did you find this?
- If the pattern goes on like this, how many barrels are there in the fifteenth picture? Call this f(15).
- How did you find this?
- If the pattern goes on like this, how many barrels are there in the n-th picture? Call this f(n).
- How did you find this?
One of the important aspects of a pattern is the way that subsequent terms are generated from previous terms. In the pattern above to go from f(1) to f(2) we add 2; to go from f(2) to f(3) we add 3; to go from f(3) to f(4) we add 4; and so on. So f(2) = f(1) + 2; f(3) = f(2) + 3; f(4) = f(3) + 4; and so on. We can see this by looking at the pictures to see how new terms are constructed.
- Can you see what is going on here?
- Can you complete these equations?
f(5) = f(4) +
f(6) = f(5) +
f(11) = f(10) +
f(20) = f(19) +
f(n) = f(n – 1) +
This last equation tells us how to get any term from the previous one. By putting in various values for n we can find the other equations that we have just looked at. So this equation is valuable and is given a special name. It is called a recurrence relation because it tells us about the recurring relation between consecutive terms. One use of this recurrence relation is that it enables us to produce a table showing the number of barrels in any term. (Though this gets a little tedious when the term number is large – like 100, say. We will see how to deal with this later in this unit.)
- For the rest of this lesson, provide time for students to look at several patterns, decide what their recurrence relations are and then construct tables of values from these recurrence relations. In each case, students should find f(n) for n = 1, 2, 3, 4, 5, and 10.
- Have students initially try Pattern 2: Odd Bricks (these are shown on Copymaster 1.2 along with instructions for the students), before trying each of the other situations of Patterns 3, 4 and 5 (see Copymasters 1.3, 1.4, and 1.5).
- Let the students work in small groups of from 2 to 4 on these problems. Roam between the groups, checking on their progress, supporting their thinking, and keeping them on track. When most of the groups have finished Pattern 2, discuss it with the whole class.
What did your group get?
Do the other groups agree?
How did you get those values? What did you have to do?
- Let the groups continue working undisturbed except for your monitoring of their progress. Groups that finish early can be asked to find f(n) for some of the patterns. Tell them that they will have to justify their answers.
Sessions 2 - 3
In this session, the class will use their tables to produce values of f(n).
Explain to students:
As you know from the last session, the recurrence relations are useful as a tool to generate a table of values. However they are of limited value if you want to find, say, f(100), as they have to be used an inordinate number of times. This could easily lead to arithmetical errors. What would be nice would be a formula for f(n) so that we could just plug in, say 100, and get f(100) with a minimum of counting. We’ll tackle this problem here.What we are about to do is just a matter of guessing. We will try to guess the formula for f(n). But we’ll try to do it systematically.
Return to Pattern 1, the Barrels. Work with students to see how you can go about finding the pattern from the table of values that has been produced.
It will help us if we look at the table and try to work from there. Notice that I’ve added a middle column that I think will help us and I’ve put in tall the values up to n = 6.n f(n) 1 1 2 3 3 6 4 10 5 15 6 21 What I want to do is to see how to get from n to f(n). To do this I’m going to use the middle column to work out f(n)/n. So let’s do that now. Use questioning and discussion to complete the table below.
n f(n)/n f(n) 1 1 1 2 3/2 3 3 2 6 4 10/4=5/2 10 5 3 15 6 21/6=7/2 21 Can you guess what the pattern of the middle column is? [(n+1)/2]
Is this an easier pattern to find than the pattern for f(n)?
So how do we get f(n) from n and this pattern of the middle column? [Multiply the pattern of the middle column by n to get f(n).]
What is f(n) then? [f(n) = n(n+1)/2.]- That’s all well and good but does it really work? Perhaps we should check a few values to give us some confidence in our guessing.
What is f(1)? What does the formula give us?
What is f(2)? What does the formula give us?
What is f(3)? What does the formula give us?
What is f(4)? What does the formula give us?
What is f(5)? What does the formula give us?
What is f(6)? What does the formula give us?
So it looks as if we have got it right.
- Have students, in their groups, use the tables to get the formula for the general terms of the patterns you have been using. Start with Pattern 2, the Odd Bricks. Check the progress of each of the groups and bring the whole class together if there are any general difficulties.
- Bring all of the class together towards the end of the lesson to discuss the results they have achieved. Accept alternative approaches to the correct formulae.
- Ask students why the formulae they have found really give the number of barrels (etc.) for the n-th term of the sequence. How can we be sure that the table really represents the physical situation that we started with?
Sessions 4-5
In this session, that may take more than one lesson, we look at a geometrical approach to finding formulae for the n-th terms of sequences. Naturally the method won’t work for all patterns but it will work for the ones that we have here and for arithmetic progressions generally.
- Explain to students: Let’s look at the Barrel problem again. I want to show you a way of finding the formula for f(n) using a geometrical approach. First I’ll make the Barrels diagram look like a right-angled diagram. Then I’ll add another copy of the right-angled diagram. This will give me a rectangle. I can find the area of a rectangle by multiplying the length by the width. From this I can get f(n). So it’s
- Change the Barrels to a right-angled shape;
- Add another copy of this shape;
- Calculate the area of the rectangle that we’ve made
- Work through this process to find the Barrels formula (see Copymaster 3.1).
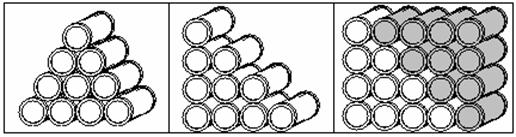
- Here is the old Barrels picture (see left hand picture above).
- Here is the Barrels picture made into a right-angled picture.
- Now let’s make another of these (middle picture), turn it upside down, and add it to the first one. This gives us a rectangle with height 4 and length 5. The area of such a rectangle is 4 x 5 = 20. So there are 20 barrels in the combined diagram (right hand picture). But we have added two lots of Barrels. So the original set of Barrels had 20/2 = 10 Barrels. This means that f(4) = 10.
Let’s run through this again with 7 rows of Barrels (see Copymaster 3.2).
Here is the first Barrels picture (top picture).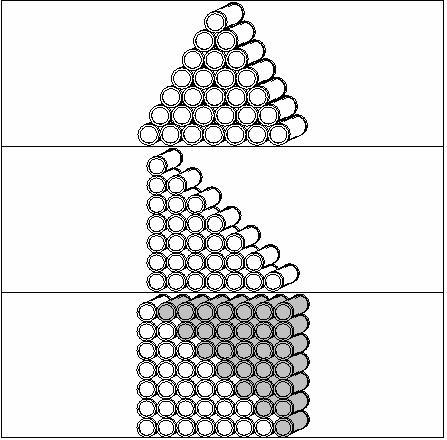
- Here is the Barrels picture made into a right-angled picture (middle picture).
- Now let’s make another of these, turn it upside down, and add it to the first one (bottom picture). This gives us a rectangle with height 7 and length 8. The area of such a rectangle is 7 x 8 = 56. So there are 56 barrels in the combined diagram (see bottom picture). But we have added two lots of Barrels. So the original set of Barrels had 56/2 = 28 Barrels. This means that f(7) = 28.
Let’s run through this again with n rows of Barrels (see Copymaster 3.3).
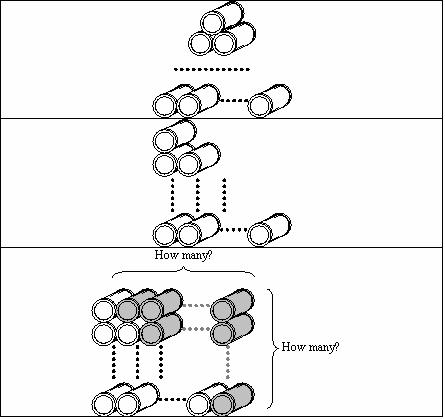
- Here is the first Barrels picture (see top picture).
- Here is the Barrels picture made into a right-angled picture.
- Now let’s make another of these (middle picture), turn it upside down, and add it to the first one. This gives us a rectangle with height n and length n + 1. The area of such a rectangle is n x (n + 1). So there are n(n + 1) barrels in the combined diagram (see bottom picture). But we have added two lots of Barrels. So the original set of Barrels had
n(n + 1)/2 Barrels. - This means that f(n) = n(n + 1)/2.
- Send the students off to work geometrically in their groups to produce the remaining patterns (f(n)). They might be given some help with the Odd Bricks Problem (see Copymasters 3.4, 3.5 and 3.6) but after that see if they know how to tackle the problems on their own. Roam and provide support as students work. Provide whole class feedback, teaching, and modelling as necessary.
- Provide time for students record, in an appropriate manner (e.g. in their books, as a flow chart, on a slide deck) what they have done.
Dear families and whānau,
Recently we have been looking at two general equations associated with a sequence or pattern: (i) recurrence relations as general ways to see what happens between consecutive terms of a sequence; and (ii) the general term of a sequence as a function of the number of that term. We have explored these using algeraic and geometric methods. Ask your child to share their learning with you.