What Goes Around ...

Problem One

The students can approach this problem in various ways. More able students will recognise this as another lowest common multiple problem. What is the lowest common multiple of 6 and 4? It’s 12. At 12 minutes, Millie will have completed exactly three laps at 4 minutes per lap and Billy will have completed exactly two laps at 6 minutes per lap. (Millie will lap Billy at the point where they started racing.)
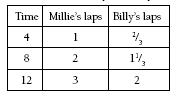
A slightly less efficient approach is to record Millie’s and Billy’s progress on a table. Students could use several different tables, depending on what is clearest for them. This table shows where Billy is each time Millie completes a lap.

If the students are having trouble grasping these concepts, this is a good problem to act out, model with equipment, or draw as a diagram.
Millie obviously takes the lead. When Billy completes his first lap, Millie has done a lap and a half. So when Billy completes two laps, Millie completes three and catches him up. This takes 2 x 6 or 3 x 4 minutes. In other words, Millie catches up in 12 minutes.
Another way to look at this is that they meet again when a multiple of 6 equals a multiple of 4.

Problem Two

This problem is similar to Problem One, page 1. The students can use the same method to find the total of the string of eight numbers, that is: sum = (2 + 9) x (8 ÷ 2)
= 11 x 4
= 44
The students have to find sets of four numbers that add up to 22. Once they have found one, the remaining four numbers add up to 22 as well, giving two sets of four numbers. It is best to do this systematically by considering 2 with every other possible number.
2 and 3: 2 + 3 = 5, so you need to make up 17 with the other two numbers in that set. You can only make up 17 with 8 and 9, so the first two sets are {2, 3, 8, 9} and the numbers that are left, {4, 5, 6, 7}.
2 + 4 = 6, so you need to make 16 with the other two numbers. You can do this with 8 + 8, 7 + 9, 6 + 10, 5 + 11, and so on. Clearly you can’t have 8 + 8 because you only have one 8 to use.
You can’t have 6 + 10 because there is no 10. So the only possibility here is 7 + 9. The two sets here are {2, 4, 7, 9} and {3, 5, 6, 8}.
2 + 5 = 7, so you need 15. 15 can only be made up here from 6 + 9 and 7 + 8. So this gives two possibilities: {2, 5, 6, 9} and {3, 4, 7, 8}; or {2, 5, 7, 8} and {3, 4, 6, 9}.
2 + 6 = 8, so you need 14. 14 can be made up from 5 + 9, 6 + 8, and 7 + 7. 5 + 9 is no good because you already had that combination {2, 5, 6, 9} in the last case. And 6 + 8 or 7 + 7 would both mean using a number twice. There are no answers here.
2 + 7 = 9, so you need 13. 13 = 4 + 9, 5 + 8, 6 + 7. You have already considered all these possible sets.
2 and 8: You have considered all these possibilities.
2 and 9: You have considered all these possibilities.
The four pairs of sets that satisfy the conditions of the question are given in the Answers.

Problem Three

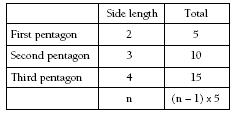
The students could use trial and improvement to solve this problem, but encourage them to look for a pattern in the length of the sides and the total number of counters. A table will help them see the pattern:

There are five sides in a pentagon, so the students might assume that to get the total number of counters they just need to multiply the side length by 5. But this doesn’t work because each corner counter is part of two sides, and multiplying the side length by 5 will mean the corner counters are counted twice. (This is a similar situation to Problem Two, page 10.) To avoid counting counters twice, the students need to subtract 1 from the side length and then multiply by 5. This will give
the general rule for any side length:

Joseph used 75 counters to make a pentagon. Applying the rule gives an answer of 16:
(n – 1) x 5 = 75
n – 1 = 75 ÷ 5
n – 1 = 15
n = 16

Problem Four

The students can find all the possible numbers by working systematically. There can only be one digit in the tens column, so the only ones and hundreds digits will be digits that multiply to give a one-digit product. For example, there can’t be a number with 3 in the hundreds column and 4 in the ones column because the product of 3 and 4 is 12, and this won’t fit in the tens column.
Take each hundreds digit in turn, starting with 1, and work out what the ones digit would be to give a tens digit that is the product of the hundreds and the ones digits. For example, a hundreds digit of 1 and a ones digit of 0 would give 0 as the tens digit, so that house number is 100. A hundreds digit of 1 with a ones digit of 1 would give 111, and so on. Work systematically through the remaining hundreds digits.
A full list is given in the Answers.
Work in a similar way for part b, although this time, the only possible ones and tens digits are those that add to a one-digit sum.

Hints for Students

1. Where is Billy after Millie’s first lap, second lap, and so on?
You could act this problem out, draw a diagram, or use equipment.
2. Can you find a more efficient strategy than trial and improvement?
Try adding all the numbers together. What will the sum of each set of four numbers
be?
3. Can you find a pattern in the number of counters in each side and the total number of counters in each pentagon?
4. Work systematically to find all the possible numbers.

Answers to Problems

1. After 12 minutes (at the end of Billy’s second lap and Millie’s third lap)
2. There are four possibilities:
2 + 3 + 8 + 9 and 4 + 5 + 6 + 7
2 + 4 + 7 + 9 and 3 + 5 + 6 + 8
2 + 5 + 6 + 9 and 3 + 4 + 7 + 8
2 + 5 + 7 + 8 and 3 + 4 + 6 + 9
3. 16
4.