Kia mōhio te ākonga:
- ki te ture mō te whakawehe hautau
- ki te whakamārama, ki te whakatauira i te wehenga o tētahi tau mā tētahi hautau
| hātepe | algorithm |
| hau-tahi | unit fraction |
| pakitau | number story |
| pou | column |
| rāwekeweke | manipulate |
| rōrahi | volume |
| tāhei | bar, strip |
| tau hanumi | mixed number |
| tauoti | whole number |
| tau taupoki | reciprocal |
| tūtohi | table |
| whakaputa | derive, produce |
| whārite taurangi | algebraic equation |
- Ko te mahi tuatahi, he tirotiro i te wehenga o te kotahi mā tētahi hau-tahi, pērā i te 1 ÷ ¼. Ka tirohia hoki te whakareatanga e whai pānga ana (¼ x 4 = 1)
- tuhi i te whārite whakawehe e hāngai ana;
- tuhi i tētahi pikitia hei whakaatu i te rapanga;
- whakaoti i te wehenga;
- tuhi i te whakareatanga e hāngai ana.
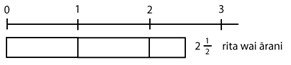
- Kotahi rita (1l) te rōrahi o te wai ārani, ka wehea ki ētahi ipu ¼ rita te kītanga. E hia ngā ipu ka taea te whakakī?
- Kotahi mita te roa o tētahi aho. Ka tapahia kia hautekau mita te roa o ngā tapahanga. E hia ngā tapahanga ka hua mai?
- Kotahi te parehe (pīta), ka tapahia kia hauwaru te rahi o ngā wehenga. E hia ngā wehenga parehe ka hua mai?
- Kotahi te poro tiakareti, ka tapahia kia haurima te rahi o ngā wehenga. E hia ngā wehenga ka hua mai?
- Ko te mahi tuarua, he tirotiro i te wehenga o te tauoti mā tētahi hau-tahi, pērā i te 5 ÷ ¼. Ka tirohia hoki te whakareatanga e whai pānga ana (¼ x 20 = 5)
- tuhi i te whārite whakawehe e hāngai ana;
- tuhi i tētahi pikitia hei whakaatu i te rapanga;
- whakaoti i te wehenga;
- tuhi i te whakareatanga e hāngai ana.
- E 3 rita (3l) te rōrahi o te wai ārani, ka wehea ki ētahi ipu ¼ rita te kītanga. E hia ngā ipu ka taea te whakakī?
- E 50 mita te roa o tētahi aho. Ka tapahia kia haurua mita te roa o ngā tapahanga. E hia ngā tapahanga ka hua mai?
- E 5 ngā parehe (pīta), ka tapahia kia hauwaru te rahi o ngā wehenga. E hia ngā wehenga parehe ka hua mai?
- 320 mita te roa o tētahi aho. Ka tapahia kia hautekau mita te roa o ngā tapahanga. E hia ngā tapahanga ka hua mai?
- I konei, ka tūhura i te wehenga o te tauoti mā tētahi hautau, ina he tauoti te otinga, pērā i te 3 ÷ ¾ = 4. Ka tirohia hoki te whakareatanga e whai pānga ana (¾ x 4 = 3)
- tuhi i te whārite whakawehe e hāngai ana;
- tuhi i tētahi pikitia hei whakaatu i te rapanga;
- whakaoti i te wehenga;
- tuhi i te whakareatanga e hāngai ana.
- E 6 rita (6l) te rōrahi o te wai ārani, ka wehea ki ētahi ipu 3/5 rita te kītanga. E hia ngā ipu ka taea te whakakī?
- E 72 mita te roa o tētahi aho. Ka tapahia kia toru hauwaru mita (3/8 m) te roa o ngā tapahanga. E hia ngā tapahanga ka hua mai?
- 12 ngā parehe (pīta), ka tapahia kia 2/3 te rahi o ngā wehenga. E hia ngā wehenga parehe ka hua mai?
- 100 mita te roa o tētahi aho. Ka tapahia kia 2/3 mita te roa o ia tapahanga. E hia ngā tapahanga ka hua mai?
- I konei, ka tūhura i te wehenga o te tauoti mā tētahi hautau, ina he tau hanumi te otinga, pērā i te 2 ÷ ¾ = 2 ⅔. Ka tirohia hoki te whakareatanga e whai pānga ana (¾ x 2 ⅔ = 2)
- tuhi i te whārite whakawehe e hāngai ana;
- tuhi i tētahi pikitia hei whakaatu i te rapanga;
- whakaoti i te wehenga;
- tuhi i te whakareatanga e hāngai ana.
- E 3 rita (3l) te rōrahi o te wai ārani, ka wehea ki ētahi ipu 2/5 rita te kītanga. E hia ngā ipu ka taea te whakakī?
- E 4 ngā kapu maramara tiakareti a Hone hei tunu keke māna. E ¾ kapu hei tunu i te keke kotahi. E hia ngā keke ka taea e ia te tunu?
- 10 ngā parehe (pīta), ka tapahia kia 3/8 te rahi o ngā wehenga. E hia ngā wehenga parehe ka hua mai?
- E 5 mita te roa o tētahi aho. Ka tapahia kia ⅔ mita te roa o ia tapahanga. E hia ngā tapahanga ka hua mai?
- I konei, ka tūhura i te wehenga o te tau hanumi mā tētahi hautau, ina he tau hanumi te otinga, pērā i te 2 ½ ÷ ¾ = 3 ⅓ . Ka tirohia hoki te whakareatanga e whai pānga ana (¾ x 3 ⅓ = 2 ½)
- tuhi i te whārite whakawehe e hāngai ana;
- tuhi i tētahi pikitia hei whakaatu i te rapanga;
- whakaoti i te wehenga;
- tuhi i te whakareatanga e hāngai ana.
- E 3 ½ rita (3 ½l) te rōrahi o te wai ārani, ka wehea ki ētahi ipu 2/5 rita te kītanga. E hia ngā ipu ka taea te whakakī?
- E 4 ¾ kg mīti a Hone hei whāngai i tana kurī. E ⅔ kg mīti hei kai mā tana kurī i ia rā. E hia ngā rā ka taea e ia tana kurī te whāngai, kia pau rā anō te mīti?
- 2 ½ ngā parehe (pīta), ka tapahia kia 3/8 te rahi o ia wehenga. E hia ngā wehenga parehe ka hua mai?
- E 5 ⅔ mita te roa o tētahi aho. Ka tapahia kia ¾ mita te roa o ia tapahanga. E hia ngā tapahanga ka hua mai?
- Ināianei, ka hoki ki te tirotiro i ngā wehenga hautau katoa kua oti i mua ake nei, me te tūhura anō i te ture mō te whakawehe i tētahi tau mā tētahi hautau.
- Ko te mahi whakamutunga, he whakaputa i te ture mō te whakawehe hautau.
| Ngā tohutohu | He Tauira Kōrero Mā Te Pouako |
| Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga.
Kotahi te poro tiakareti a Mareta. E hiahia ana ia kia wehea tana poro tiakareti, kia haurua te rahi o ngā wehenga. E hia ngā wehenga ka hua mai? Aratakina ngā ākonga ki te whiriwhiri i te otinga. |
He aha te whārite e hāngai ana ki te rapanga nei? E wehea ana te kotahi mā te haurua, arā, 1 ÷ ½ = □ He tāhei tēnei hei tohu i te poro tiakareti: He tāhei tēnei hei tohu i te haurua poro tiakareti: Mēnā ka whakatakotoria ngā haurua ki raro i te kotahi, he mārama te kitea, ina wehea te kotahi mā te haurua, ko te rua te otinga. 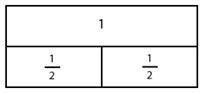 Nō reira, he aha te otinga o te whārite? 1 ÷ ½ = 2 He aha te whakareatanga e hāngai ana? E rua ngā haurua kei roto i te kotahi, arā, ½ x 2 = 1 |
| Tukuna ngā ākonga ki te tūhura i ngā rapanga nei. Tonoa rātou ki te:
|
|
| Ngā tohutohu | He Tauira Kōrero Mā Te Pouako |
| Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga.
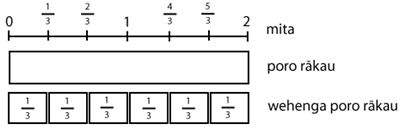
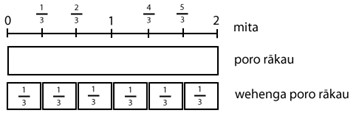
E 2 mita te roa o te poro rākau a Hinewai. E hiahia ana ia kia tapahia tana poro rākau, kia hautoru mita te roa o ngā tapahanga. E hia ngā wehenga ka hua mai? Aratakina ngā ākonga ki te whiriwhiri i te otinga. |
He aha te whārite e hāngai ana ki te rapanga nei? E wehea ana te rua mā te hautoru, arā, 2 ÷ ⅓ = □
He tāhei tēnei hei tohu i te poro rākau:
Mēnā ka tapahia te poro rākau kia hautoru mita te roa o ngā wehenga, e 6 katoa ngā wehenga ka hua mai:
Nō reira, he aha te otinga o te whārite? 2 ÷ ⅓ = 6 He aha te whakareatanga e hāngai ana? E ono ngā hautoru kei roto i te rua, arā, ⅓ x 6 = 2 |
| Tukuna ngā ākonga ki te tūhura i ngā rapanga nei. Tonoa rātou ki te:
|
|
| Ngā tohutohu | He Tauira Kōrero Mā Te Pouako |
| Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga.
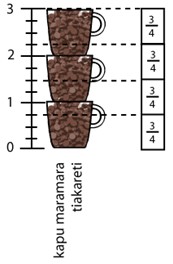
E 3 ngā kapu maramara tiakareti a Hone hei tunu keke māna. E ¾ kapu hei tunu i te keke kotahi. E hia ngā keke ka taea e ia te tunu? Aratakina ngā ākonga ki te whiriwhiri i te otinga. |
He aha te whārite e hāngai ana ki te rapanga nei? E wehea ana te toru mā te toru hauwhā, arā, 3 ÷ ¾ = □
E toru ngā kapu maramara tiakareti e whakaaturia ana i tēnei pikitia. Kua wāwāhia ki ngā wehenga ¾ kapu te rōrahi. E 4 katoa ngā ¾ kei roto i te 3:
Nō reira, he aha te otinga o te whārite? 3 ÷ ¾ = 4 He aha te whakareatanga e hāngai ana? E whā ngā toru hauwhā kei roto i te toru, arā, ¾ x 4 = 3 |
| Tukuna ngā ākonga ki te tūhura i ngā rapanga nei. Tonoa rātou ki te:
|
|
| Ngā tohutohu | He Tauira Kōrero Mā Te Pouako |
| Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga.
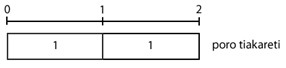
E 2 ngā poro tiakareti a Hone hei wehewehe māna kia ¾ te rahi o ia wehenga. E hia ngā wehenga tiakareti ka hua mai? Aratakina ngā ākonga ki te whiriwhiri i te otinga. |
He aha te whārite e hāngai ana ki te rapanga nei? E wehea ana te rua mā te toru hauwhā, arā, 2 ÷ ¾ = □
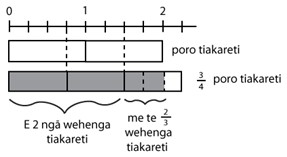
E rua ngā poro tiakareti e whakaaturia ana i tēnei pikitia:
Kua wāwāhia ki ngā wehenga ¾ te rahi. E 2 ⅔ ngā ¾ kei roto i te 2:
Nō reira, he aha te otinga o te whārite? 2 ÷ ¾ = 2 ⅔ He aha te whakareatanga e hāngai ana? E rua me te rua hautoru ngā toru hauwhā kei roto i te rua, arā, ¾ x 2 ⅔ = 2 |
| Tukuna ngā ākonga ki te tūhura i ngā rapanga nei. Tonoa rātou ki te:
|
|
| Ngā tohutohu | He Tauira Kōrero Mā Te Pouako |
| Tuhia te rapanga nei ki te papa tuhituhi, ka pānui tahi ai me ngā ākonga.
E rua me te haurua rita (2 ½ l) te rōrahi o te wai ārani, ka wehea ki ētahi ipu ¾ rita te kītanga. E hia ngā ipu ka taea te whakakī? Aratakina ngā ākonga ki te whiriwhiri i te otinga. |
He aha te whārite e hāngai ana ki te rapanga nei? E wehea ana te rua me te haurua mā te toru hauwhā, arā, 2 ½ ÷ ¾ = □
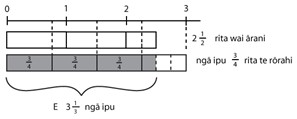
He tāhei tēnei e tohu ana i te 2 ½ rita wai ārani:
Kua wehea te 2 ½ ki ētahi ipu e toru hauwhā rita (¾) te rōrahi. E 3 ⅓ ngā ipu ka taea te whakakī:
Nō reira, he aha te otinga o te whārite? 2 ½ ÷ ¾ = 3 ⅓ He aha te whakareatanga e hāngai ana? E toru me te kotahi hautoru ngā toru hauwhā kei roto i te rua me te haurua, arā, ¾ x 3 ⅓ = 2 ½ |
| Tukuna ngā ākonga ki te tūhura i ngā rapanga nei. Tonoa rātou ki te:
|
|
| Ngā tohutohu | He Tauira Kōrero Mā Te Pouako | |||||||||||||||||||||||||||||||||||||||
| E hoki ki te tirotiro i ētahi o ngā wehenga kua oti i tēnei kōwae ako, me te whakaatu anō i te hatepe hei whakawehe i tētahi tau mā tētahi hautau. | Koia nei tētahi o ngā wehenga i oti i a tātou, me te pikitia e hāngai ana: 2 ÷ ⅓ = 6 Ka taea ngā tauoti o te whārite te huri hei hautau:
Ināianei, ka hurihia te wehenga hei whakareatanga, ā, ka huri taupoki i te hautau tuarua o te whārite. Ka puta tētahi tauira, arā, ka tika tonu te whakareatanga:
E kitea ana te tika o te whakareatanga. |
|||||||||||||||||||||||||||||||||||||||
Kia pērā anō te huri i ētahi atu o ngā wehenga kua oti i tēnei kōwae ako. Kua oti ētahi o ngā whārite i raro nei hei tauira:
|
||||||||||||||||||||||||||||||||||||||||
| Āta tirohia te tauira e puta ake ana i ngā whārite, ka whakawhitiwhiti kōrero mō te ture hei whakaoti wehenga. | I te pou tuatoru o te tūtohi, i hurihia ngā wehenga hei whakareatanga, ā, i huri taupoki anō hoki te hautau tuarua o te whārite. He tika katoa ngā whakareatanga i te pou tuatoru nei? Āe, kei te tika katoa.
Nō reira, kua kitea he huarahi hei whakaoti wehenga. Arā, hurihia te wehenga hei whakareatanga, me te huri taupoki anō i te hautau tuarua o te whārite. Hei tauira:
|
|||||||||||||||||||||||||||||||||||||||
Hoatu ētahi atu rapanga wehe hei whakaoti mā ngā ākonga. Tonoa hoki rātou ki te tuhi pakitau e hāngai ana ki te whārite. Hei tauira:
|
||||||||||||||||||||||||||||||||||||||||
| Ngā tohutohu | He Tauira Kōrero Mā Te Pouako |
| Āta whakamārama i te whakaputanga o te ture mō te whakawehe hautau.
Me āta whakamārama ia hīkoi: Mēnā ka ōrite te rāwekeweke i ia taha o te tohu ‘=’, ka tika tonu te whārite. Hei tauira: |
Anei tētahi wehenga hautau, hei tirotiro mā tātou:
3/4 ÷ 5/6 = □ Ka rāwekeweke haere tātou i te whārite nei, kia kitea he aha e tika ai te ture nei mō te whakawehe hautau: Tuatahi, ka hurihia te wehenga hei whakareatanga: 5/6 x □ = 3/4 Tuarua, ka whakareatia ia taha o te whārite ki te 6/5. Ko te 6/5 te tau taupoki o te 5/6: 6/5 x 5/6 x □ = 3/4 x 6/5 Ko te take i whakareatia te 5/6 ki te 6/5, kia huri i te tau whakarea i te pouaka ki te tahi. Arā: 30/30 x □ = 3/4 x 6/5 He ōrite te 30/30 ki te 1, nō reira: □ = 3/4 x 6/5 Kia tīkina atu te whārite wehe i te tīmatanga: 3/4 ÷ 5/6 = □ Nō reira: 3/4 ÷ 5/6 = 3/4 x 6/5 |
| Tukuna ngā ākonga ki te whai i tēnei rāwekeweketanga mō ētahi atu whārite wehenga hautau.
Whakawhitiwhiti kōrero mō te tika o te ture, ahakoa he aha te whārite wehenga hautau. |
Kia pērā anō tō rāwekeweke i ngā whārite wehenga nei:
2/3 ÷ 1/2 = □ 5/3 ÷ 3/4 = □ Ahakoa te whārite, e kite ana tātou i te tika o te ture mō te whakawehe hautau, arā: |
Hei Whakawhānui:
Tirohia te rāwekeweketanga o te wehenga hautau taurangi nei:
a/h ÷ e/k
hei whakaputa i te ture hei whārite taurangi:
a/h ÷ e/k = a/h x e/k