This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (412 KB)
find a percentage of a whole number
solve problems involving percentages
FIO, Level 3-4, Number, Book 3, Water World, pages 18-19
A classamte
Activity One
This activity focuses on percentages in the context of water. Students will need to have strong multiplicative strategies to answer the questions in this activity, which is suitable for students at the advanced multiplicative stage or beyond of the Number Framework. Make sure your students understand that percent (%) means out of 100, with 100 as the whole. So 70% is 70/100.
Students are often surprised to learn that water makes up a considerable percentage of the human body and the bodies of other mammals and of fruit and vegetables. They may not realise, either, just how much water or moisture we lose from our body in a day. Some long-distance athletes find out the hard way (through experiencing the debilitating effects of dehydration) that it is vital to continuously replace water lost through activity. Water World is an excellent activity for highlighting the importance of water in our lives.
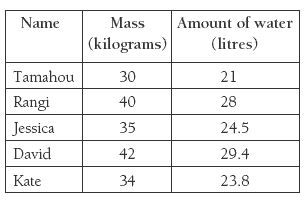
Activity One provides the information that 1 litre of water weighs 1 kilogram. This is true of pure fresh water (although not of salty sea water), so it is relevant to the water in our bodies. Tamahou suggests that 70% be calculated by first finding 10% (1/10) and then multiplying this amount by 7. This is a good strategy, and although it will involve decimals in most cases, it shouldn’t be too difficult. For example, in Jessica’s case, 1/10 of her mass is 3.5 kilograms, so 7/10 or 70% will be 3.5 x 7. Using a part–whole strategy, the students can work this out mentally: 7 x 3 = 21 and
7 x 0.5 = 3.5, so 70% is 24.5 kilograms. The students will need to use their knowledge of equivalence between fractions, decimals, and percentages, for example, 10% = 1/10.
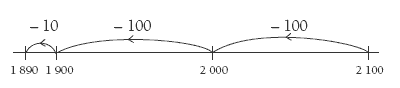
The students will need to use the data from question 1 to find the amount of water each student needs to replace in question 2. Tamahou, Jessica, and David each need to replace 9% of their water content, and Rangi and Kate need to replace 8%. Thus, the task becomes one of calculating 9% of 21 litres, 8% of 28 litres, and so on. Encourage the students to use number sense and mental strategies where possible. For example, 9% is 1% less than 10%. Tamahou’s water content is 21
litres, 10% of that is 2.1 litres, and 1% is 0.21 litres. (The students’ understanding of place value is important here.) So the problem becomes 2.1 – 0.21, which the students would be able do more easily if they work in millilitres and use a number line:
1 890 millilitres is 1.89 litres. All the problems in this question can be worked out in the same way, with 8% being seen as 10% – 1% – 1%.
In question 3, the easiest strategy for the students to use to work out the land area is to recognise that it comprises 28% of the Earth’s 500 million square kilometre surface area. Finding 28% of a large number like 500 000 000 need not be daunting if the students recognise that they only need to find 28% of 500 and call their answer millions. Encourage them to look for a number strategy rather than use a calculator. For example, using an earlier strategy, they could find 10% of 500, which is 50, and multiply that by 2 to get 20%. To find the 8%, they could use the same method
suggested for question 3, which in this case would be 50 – 5 – 5 = 40. So 28% of 500 million is 50 + 50 + 40 = 140 million.
Activity Two
Question 1 in this activity gives various percentages of water used in parts of the household. In question 1a, the students are asked to estimate the percentages of 400 litres. To do this, they could think of the percentages as fractions or approximate fractions. Thus, 10% used in the kitchen is 1/10, and 1/10 of 400 is 40 litres. The 19% used outside is about 20% and so is the 21% used in the laundry, so the easiest calculation is to double the 10% calculated for the kitchen. The 24% used in the bathroom and the 26% used in the toilet are each about 25% or 1/4, which is approximately 100 litres.
In question 1b, the 43 litres is 10% (or 1/10) of the total, so it follows that the total will be 10 times 43, which is 430 litres. In question 1c, the bathroom and toilet combined account for 50% of water usage (24% + 26%), so the students need to realise that the figure of 186 litres has to be doubled (200 + 160 + 12 = 372 litres) to find the total household usage per day.
Question 2 requires the students to refer back to the average household of question 1a and reduce the 400 litres by 20%, that is, to take off 1/5 (80 litres). Alternatively, they could find 80% of 400. This can be done mentally by either subtracting 80 litres (20% of 400) from 400 litres or multiplying 80 litres by 4 (as the reduced amount will be 4/5 of the original 400 litres). Either way, the result is 320 litres. To tackle question 2b, the students can use the same estimation strategies they used in question 1a.
Question 3 is useful for making sure that the students understand what percentages are and how to calculate them. The 10 litres is the whole (100%), so the students need to find what percentage 100 millilitres is of 10 litres. If they understood that the 70% in Activity One was 70/100, they can transfer this to 100 mL/10 L. However, to work this out, they first need to either convert the 100 millilitres to litres or the 10 litres to millilitres. In the first case, the 100 millilitres is 0.1 litres, so the problem becomes 0.1/10 = /100, which is 1%. In the second case, the 10 litres converts to
10 000 millilitres, so the problem becomes 100/10 000 = /100, which again is 1%. This means that there is a 99% saving of water during teeth brushing if you take the wet-your-brush-and-rinse quickly option.
Answers to Activities
Activity One
1.
2.
3. Methods may vary.
28% of 500 million = 140 million square km
Activity Two
1. a. Possible estimates are:
kitchen: 40 L
outside: 80 L (19% is close to 20%)
laundry: 80 L (21% is close to 20%, too)
bathroom: 100 L (24% is close to 25%)
toilet: 100 L (26% is close to 25%)
b. 430 L
c. 372 L
2. a. 320 L
b. Possible estimates, based on the same strategies as 1a, are:
kitchen: 32 L, outside: 64 L, laundry: 64 L, bathroom: 80 L, toilet: 80 L
3. 1%